

沪科版八年级数学下学期核心考点精讲精练 期末模拟(二)-【专题重点突破】(原卷版+解析)
展开考试范围:第16-20章
1.(本题4分)(2022·河南平顶山·九年级期末)下列方程是一元二次方程的是( )
A.B.C.D.
2.(本题4分)(2023·上海市久隆模范中学七年级期末)若有意义,则能取的最小整数是( ).
A.B.C.0D.1
3.(本题4分)(2022·重庆·模拟预测)若一个多边形的内角和为720°,则该多边形为( )边形.
A.四B.五C.六D.七
4.(本题4分)(2023·海南三亚·八年级期末)下列运算中正确的是( )
A.B.C.D.
5.(本题4分)(2022·山东·武城县教育教学研究中心八年级期末)一个正多边形的一个外角是,则该正多边形的内角和是( )
A.B.C.D.
6.(本题4分)(2022·福建泉州·八年级期末)《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A. B. C.D.
7.(本题4分)(2023·四川眉山·一模)某企业车间有50名工人,某一天他们生产的机器零件个数统计如表:表中表示零件个数的数据中,众数、中位数分别是( )
A.7个,7个B.7个,6个C.22个,22个D.8个,6个
8.(本题4分)(2023·广东·陆丰市甲东镇钟山中学八年级期中)如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则点C的坐标为( )
A.(3,4)B.(4,3)C.(2,3)D.(2,4)
9.(本题4分)(2022·河南洛阳·九年级期末)如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24cm2的有盖的长方体铁盒,则剪去的正方形的边长为( )
A.cmB.1cmC.cmD.2cm
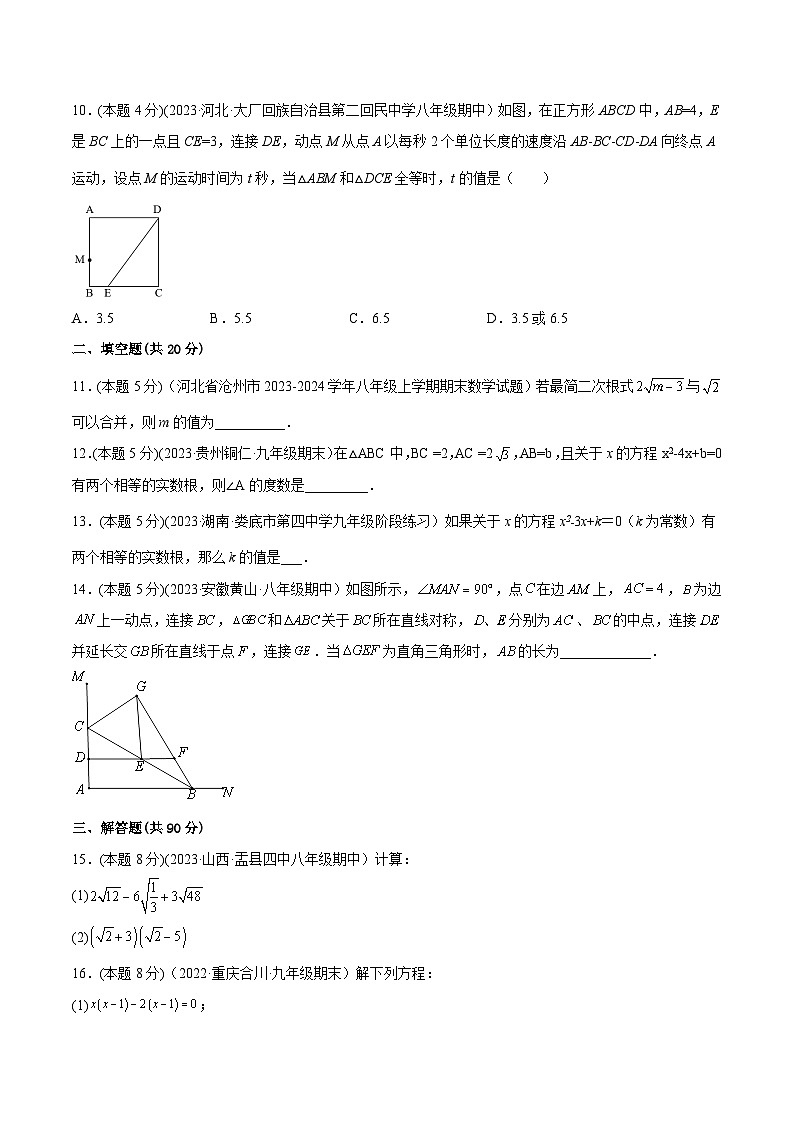
10.(本题4分)(2023·河北·大厂回族自治县第二回民中学八年级期中)如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB-BC-CD-DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5B.5.5C.6.5D.3.5或6.5
二、填空题(共20分)
11.(本题5分)(河北省沧州市2023-2024学年八年级上学期期末数学试题)若最简二次根式与可以合并,则m的值为__________.
12.(本题5分)(2023·贵州铜仁·九年级期末)在△ABC中,BC =2,AC =2,AB=b,且关于x的方程x2-4x+b=0有两个相等的实数根,则∠A的度数是_________.
13.(本题5分)(2023·湖南·娄底市第四中学九年级阶段练习)如果关于x的方程x2﹣3x+k=0(k为常数)有两个相等的实数根,那么k的值是___.
14.(本题5分)(2023·安徽黄山·八年级期中)如图所示,,点在边上,,为边上一动点,连接,和关于所在直线对称,分别为、的中点,连接并延长交所在直线于点,连接.当为直角三角形时,的长为_____________.
三、解答题(共90分)
15.(本题8分)(2023·山西·盂县四中八年级期中)计算:
(1)
(2)
16.(本题8分)(2022·重庆合川·九年级期末)解下列方程:
(1);
(2).
17.(本题8分)(2022·福建省福州屏东中学八年级期末)如图,在等腰直角△ABC中,,,点D是CA延长线上一点,点E是AB延长线上一点,且,过点A作DE的垂线交DE于点F,交BC的延长线于点G.
(1)当,求∠AGC的度数;
(2)用等式表示线段CG与AD之间的数量关系,并证明.
18.(本题8分)(2022·吉林长春·八年级期末)图①、图②都是的正方形网格,每个小正方形的边长均为,每个小正方形的顶点叫做格点,线段的端点都在格点上.在给定的网格中,只用无刻度的直尺,在图①、图②中,按下列要求画图,所画的图形的顶点均在格点上.
(1)在图①中画一个以为腰的等腰三角形;
(2)在图②中画一个以为底边的等腰三角形.
19.(本题10分)(2022·福建·厦门一中九年级期中)已知关于x的一元二次方程.
(1)求证:无论m为何值,方程总有两个实数根;
(2)若方程只有一个根为正数,求m的取值范围.
20.(本题10分)(2022·湖南·道县朝阳学校八年级阶段练习)如图,已知四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,求证:BE=DF.
21.(本题12分)(2023·河南·三模)某学校开展防疫知识宣传教育活动,为了解这次活动的效果,学校从七、八年级现有各400名的学生中随机抽取学生进行调查,过程如下:
从七、八年级各随机抽取20名学生,进行防疫知识测试,测试成绩(百分制)如下:
七年级:85 79 89 83 89 98 68 89 79 59 99 87 85 89 97 86 89 90 89 77
八年级:71 94 87 92 55 94 98 78 86 94 62 99 94 51 88 97 94 98 85 91
(1)按如下频数分布表整理描述这两组样本数据.请补全七年级20名学生测试成绩的频数分布表;
(说明:成绩为90分及以上为优秀,80~89分为良好,80分以下为不合格)
(2)两组样本数据的平均数、中位数、众数优秀率如表所示,请补充完整;
(3)若八年级学生全部参加这次考试,试估计八年级成绩优秀的学生人数;
(4)整体成绩较好的年级为哪个?理由是什么?(至少从两个不同的角度说明合理性)
22.(本题12分)(2023·山东泰安·三模)端午节临近,某商店推出白水粽和红豆粽,其中红豆粽的销售单价是白水粽的1.25倍,4月份,红豆粽和白水粽共销售150千克,红豆粽的销售额是1200元,白水粽的销售额为1440元.
(1)求红豆粽、白水粽的销售单价各是多少?
(2)为迎接端午节到来,该蛋糕店在5月推出“粽享会员”活动,对所有的粽子均可享受a%的折扣,非“粽享会员”需要按照原价购买,就红豆粽而言,5月销量比4月销量增加了a%,其中通过“粽享会员”购买的销量占5月红豆粽销量的,而5月红豆粽的销售总额比4月红豆粽销售额提高了a%,求a的值.
23.(本题14分)(2023年河北省石家庄市中考数学一模试卷)如图,在边长为6的正方形ABCD中,点M为对角线BD上任意一点(可与B,D重合),将线段AM绕点A逆时针旋转90°得到线段AN,连接MN,设BM=x.
(1)求证:△ABM≌△ADN;
(2)当时,求MN的长;
(3)嘉淇同学在完成(1)后有个想法:“△ABM与△MND也会存在全等的情况”,请判断嘉淇的想法是否正确,请直接写出△ABM与△MND全等时x的值;若不正确,请说明理由.
题号
一
二
三
总分
得分
评卷人
得分
一、单选题(共40分)
零件个数(个)
6
7
8
人数(人)
15
22
13
年级
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
七年级
1
1
11
八年级
2
1
2
4
11
年级
平均数
中位数
众数
优秀率
七年级
85.3
88
89
八年级
85.4
94
55%
2023-2024学年沪科版八年级下册期末模拟(二)
考试时间:120分钟;满分:150分
考试范围:第16-20章
1.(本题4分)(2022·河南平顶山·九年级期末)下列方程是一元二次方程的是( )
A.B.C.D.
【答案】B
【解析】
【分析】
根据一元二次方程的定义,对各个选项逐个分析,即可得到答案.
【详解】
是一元三次方程,故选项A不符合题意;
是一元二次方程,故选项B符合题意;
是二元二次方程,故选项C不符合题意;
∵
∴经移项并合并同类项,得:,即
∴是一元一次方程,故选项D不符合题意;
故选:B.
【点睛】
本题考查了一元二次方程的知识;解题的关键是熟练掌握一元二次方程的定义:只含有一个未知数,并且未知数项的最高次数是2的整式方程叫做一元二次方程.
2.(本题4分)(2023·上海市久隆模范中学七年级期末)若有意义,则能取的最小整数是( ).
A.B.C.0D.1
【答案】C
【解析】
【分析】
根据二次根式的被开方数的非负性求出的取值范围,由此即可得.
【详解】
解:由题意得:,
解得,
则能取的最小整数是0,
故选:C.
【点睛】
本题考查了二次根式有意义的条件,熟练掌握二次根式有意义的条件是解题关键.
3.(本题4分)(2022·重庆·模拟预测)若一个多边形的内角和为720°,则该多边形为( )边形.
A.四B.五C.六D.七
【答案】C
【解析】
【分析】
根据多边形内角和公式(n﹣2)•180°,求解即可.
【详解】
解:设多边形为n边形,由题意,得
(n﹣2)•180°=720°,
解得n=6,
故选:C.
【点睛】
本题主要考查多边形内角和公式,熟练地掌握计算公式是解决本题的关键.
4.(本题4分)(2023·海南三亚·八年级期末)下列运算中正确的是( )
A.B.C.D.
【答案】A
【解析】
【分析】
由二次根式的乘法、合并同类二次根式、二次根式的除法、乘方运算分别进行判断,即可得到答案.
【详解】
解:A、,正确;
B、、不是同类二次根式,不能合并,故B错误;
C、,故C错误;
D、,故D错误;
故选:A.
【点睛】
本题考查了二次根式的乘法、除法运算,以及二次根式的加法运算,乘方运算,解题的关键是掌握运算法则,正确进行计算.
5.(本题4分)(2022·山东·武城县教育教学研究中心八年级期末)一个正多边形的一个外角是,则该正多边形的内角和是( )
A.B.C.D.
【答案】A
【解析】
【分析】
根据多边形的边数与多边形的外角的个数相等,可求出该正多边形的边数,再由多边形的内角和公式求出其内角和.
【详解】
解:该正多边形的边数为:360°÷60°=6,
该正多边形的内角和为:(6-2)×180°=720°.
故选:A.
【点睛】
本题考查了多边形的内角与外角,熟练掌握多边形的外角和与内角和公式是解答本题的关键.
6.(本题4分)(2022·福建泉州·八年级期末)《九章算术》中有一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:如图,一根竹子原高1丈(1丈=10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?若设折断处离地面x尺,则下面所列方程正确的是( )
A. B. C.D.
【答案】D
【解析】
【分析】
根据题意结合勾股定理列出方程即可.
【详解】
解:设折断处离地面x尺,
根据题意可得:x2+32=(10-x)2,
故选:D.
【点睛】
本题主要考查了勾股定理的应用及由实际问题抽象出一元二次方程的知识,根据题意正确应用勾股定理是解题关键.
7.(本题4分)(2023·四川眉山·一模)某企业车间有50名工人,某一天他们生产的机器零件个数统计如表:表中表示零件个数的数据中,众数、中位数分别是( )
A.7个,7个B.7个,6个C.22个,22个D.8个,6个
【答案】A
【解析】
【分析】
根据众数、中位数的概念求解答案.
【详解】
解:这50名工人某一天生产零件个数出现次数最多的是7个,共出现22次,因此众数是7个,
将这50名工人某一天生产零件个数从小到大排列后,处在中间位置的两个数都是7个,因此中位数是7个,
故选:A.
【点睛】
本题考查众数、中位数的概念.众数是一组数据中出现最多的那个数.中位数是一组数据按照从大到小排列,位于中间位置的数就是这组数据的中位数.解题关键是准确理解概念,注意中位数一定要先排序.
8.(本题4分)(2023·广东·陆丰市甲东镇钟山中学八年级期中)如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则点C的坐标为( )
A.(3,4)B.(4,3)C.(2,3)D.(2,4)
【答案】A
【解析】
【分析】
先由四边形OABC是菱形得到, ,然后过点B作设可表示出OA、AD,利用勾股定理即可求得的长,则可得C点的坐标.
【详解】
解:过点B作于D,
∵四边形OABC是菱形,
∴,,
设,
则,,
在Rt△ABD中,
即,
解得,
,
∴C点的坐标为(3,4).
故选:A.
【点睛】
本题考查了菱形的性质与勾股定理的应用,解题的关键是方程思想与数形结合思想的应用.
9.(本题4分)(2022·河南洛阳·九年级期末)如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积是24cm2的有盖的长方体铁盒,则剪去的正方形的边长为( )
A.cmB.1cmC.cmD.2cm
【答案】D
【解析】
【分析】
设剪去的正方形的边长为xcm,则制成有盖的长方体铁盒的底面长为(10-2x)cm,宽为(6-x)cm,根据长方体铁盒的底面积是24cm2,即可得出关于x的一元二次方程,解之取其符合题意的值即可得出结论.
【详解】
解:设剪去的正方形的边长为xcm,则制成有盖的长方体铁盒的底面长为(10-2x)cm,宽为cm,
依题意得:,
整理得:,
解得:(不合题意,舍去).
故选:D.
【点睛】
本题考查长方体的展开图,一元二次方程的实际应用.根据题意找出等量关系,列出等式是解题关键.
10.(本题4分)(2023·河北·大厂回族自治县第二回民中学八年级期中)如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB-BC-CD-DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5B.5.5C.6.5D.3.5或6.5
【答案】D
【解析】
【分析】
分两种情况进行讨论,根据题意得出BM=2t-4=3和AM=16-2t=3即可求得.
【详解】
解:如图,当点M在BC上时,
∵△ABM′和△DCE全等,
∴BM=CE,
由题意得:BM′=2t-4=3,
所以t=3.5(秒);
当点M在AD上时,
∵△ABM″和△CDE全等,
∴AM″=CE,
由题意得:AM″=16-2t=3,
解得t=6.5(秒).
所以,当t的值为3.5秒或6.5秒时.△ABM和△DCE全等.
故选:D.
【点睛】
本题考查了正方形的性质、全等三角形的判定,解题的关键是掌握正方形的性质.
11.(本题5分)(河北省沧州市2023-2024学年八年级上学期期末数学试题)若最简二次根式与可以合并,则m的值为__________.
【答案】5
【解析】
【分析】
根据同类二次根式的定义,列式子整理即可得解;
【详解】
解:由题意得:m-3=2,m=5,
故答案为:5;
【点睛】
本题考查同类二次根式的概念,同类二次根式是化为最简二次根式后,被开方数相同的二次根式.
12.(本题5分)(2023·贵州铜仁·九年级期末)在△ABC中,BC =2,AC =2,AB=b,且关于x的方程x2-4x+b=0有两个相等的实数根,则∠A的度数是_________.
【答案】30º
【解析】
【分析】
由根的判别式求出AB=b=4,由勾股定理的逆定理证出△ABC是直角三角形,再由含30º直角三角形性质,即可得出结论.
【详解】
解:∵关于x的方程x2﹣4x+b=0有两个相等的实数根,
∴△=16﹣4b=0,
∴AB=b=4,
∵BC=2,AC=2 ,
∴BC2+AC2=AB2,
∴△ABC是直角三角形,AB是斜边,
∵AB=4, BC=2;
∴∠A=30º
故答案为:∠A=30º
【点睛】
本题考查了根的判别式,勾股定理的逆定理,含30º直角三角形性质;证明△ABC是直角三角形是解决问题的关键.
13.(本题5分)(2023·湖南·娄底市第四中学九年级阶段练习)如果关于x的方程x2﹣3x+k=0(k为常数)有两个相等的实数根,那么k的值是___.
【答案】
【解析】
【分析】
根据判别式的意义得到Δ=(-3)2-4k=0,然后解一元一次方程即可.
【详解】
解:根据题意得Δ=(-3)2-4k=0,
解得k=.
故答案为.
【点睛】
本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2-4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.
14.(本题5分)(2023·安徽黄山·八年级期中)如图所示,,点在边上,,为边上一动点,连接,和关于所在直线对称,分别为、的中点,连接并延长交所在直线于点,连接.当为直角三角形时,的长为_____________.
【答案】4或##或4
【解析】
【分析】
当△为直角三角形时,存在两种情况:①当时,如图1,根据对称的性质和平行线可得:,根据直角三角形斜边中线的性质得:,最后利用勾股定理可得的长;②当时,如图2,证明是等腰直角三角形,可得.
【详解】
解:当△为直角三角形时,存在两种情况:
①当时,如图1,
△与关于所在直线对称,
,,
点,分别为,的中点,
、是的中位线,
,
,
,
,
,
,
,
△中,
是斜边的中点,
,
由勾股定理得:,
;
②当时,如图2,
,
,
△与关于所在直线对称,
,
是等腰直角三角形,
;
综上所述,的长为或4.
故答案为:或4.
【点睛】
本题考查了三角形的中位线定理、勾股定理、轴对称的性质、等腰直角三角形的判定、直角三角形斜边中线的性质,解题的关键是掌握相应的定理并利用分类讨论的思想解决问题.
15.(本题8分)(2023·山西·盂县四中八年级期中)计算:
(1)
(2)
【答案】(1)
(2)
【解析】
【分析】
【小问1分析】
把12化成,化成,48化成,在把4,,16开方出来,最后合并.
【小问2分析】
先按多项式乘多项式的法则展开,再分别合并有理数部分与部分.
(1)
.
(2)
.
【点睛】
本题主要考查了实数的运算,二次根式的化简,最简二次根式.解决问题的关键是深刻理解最简二次根式的概念,熟练分解出能开得尽方的因式(因数),分母有理化因式(因数),合并同类二次根式.(1)先把各个根式化简,再合并最简同类二次根式.(2)先按多项式乘多项式的法则展开,再分别合并有理数与无理数.
16.(本题8分)(2022·重庆合川·九年级期末)解下列方程:
(1);
(2).
【答案】(1)x1=1,x2=2;
(2)x1=8,x2=-1.
【解析】
【分析】
(1)将左边利用提公因式法因式分解,继而可得两个关于x的一元一次方程,分别求解即可得出答案;
(2)先移项,再将左边利用十字相乘法因式分解,继而可得两个关于x的一元一次方程,分别求解即可得出答案.
(1)
解:∵x(x-1)-2(x-1)=0,
∴(x-1)(x-2)=0,
则x-1=0或x-2=0,
解得x1=1,x2=2;
(2)
解:∵x2-8=7x,
∴x2-7x-8=0,
则(x-8)(x+1)=0,
∴x-8=0或x+1=0,
解得x1=8,x2=-1.
【点睛】
本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.
17.(本题8分)(2022·福建省福州屏东中学八年级期末)如图,在等腰直角△ABC中,,,点D是CA延长线上一点,点E是AB延长线上一点,且,过点A作DE的垂线交DE于点F,交BC的延长线于点G.
(1)当,求∠AGC的度数;
(2)用等式表示线段CG与AD之间的数量关系,并证明.
【答案】(1)25°
(2),理由见解析
【解析】
【分析】
(1)根据∠BAC=90°,,可得∠DAE=90°,∠ABC=∠ACB=45°,再由AF⊥DE,可得∠DAF=∠AED=20°,从而得到∠CAG=20°,再由三角形外角的性质,即可求解;
(2)过点E作EH⊥AE于点E,交CB延长线于点H,可得BE=HE,根据勾股定理可得BH=BE,从而得到BH=AD,再证得△AEH≌△EAD,可得∠BAH=∠AED=∠DAF=∠CAG,再证得△ABH≌△ACG,即可求解.
(1)
解:∵∠BAC=90°,,
∴∠DAE=90°,∠ABC=∠ACB=45°,
∴∠D+∠AED=90°,
∵AF⊥DE,
∴∠D+∠DAF=90°,
∴∠DAF=∠AED=20°,
∴∠CAG=20°,
∵∠ACB=∠CAG+∠AGC,
∴∠AGC=25°;
(2)
解:,理由如下:
如图,过点E作EH⊥AE于点E,交CB延长线于点H,
∴∠BEH=90°,∠EBH=∠ABC=45°,
∴∠BHE=∠EBH=45°,
∴BE=HE,
∴AD=BE=HE,
∴BH2=BE2+HE2=2BE2,
∴BH=BE,
∵AD=BE,
∴BH=AD,
在△AEH和△EAD中,
∵EH=AD,∠AEH=∠EAD=90°,AE=EA,
∴△AEH≌△EAD(SAS),
∴∠BAH=∠AED=∠DAF=∠CAG,
∵∠ABH=180°-∠ABC=135°,∠ACG=180°-∠ACB=135°,
∴∠ABH=∠ACG,
在△ABH和△ACG中,
∵∠BAH=∠CAG, AB=AC,∠ABH=∠ACG,
∴△ABH≌△ACG(ASA),
∴BH=CG,
∴CG=AD.
【点睛】
本题主要考查了等腰三角形的性质,勾股定理,全等三角形的判定和性质,熟练掌握等腰三角形的性质,勾股定理,全等三角形的判定和性质是解题的关键.
18.(本题8分)(2022·吉林长春·八年级期末)图①、图②都是的正方形网格,每个小正方形的边长均为,每个小正方形的顶点叫做格点,线段的端点都在格点上.在给定的网格中,只用无刻度的直尺,在图①、图②中,按下列要求画图,所画的图形的顶点均在格点上.
(1)在图①中画一个以为腰的等腰三角形;
(2)在图②中画一个以为底边的等腰三角形.
【答案】(1)见详解;
(2)见详解;
【解析】
【分析】
(1)A点在B点上方第三个格子,因此可以在B点右边第三个格子寻找一格点使BC=BA(答案不唯一;
(2)可以在线段AB右侧寻找一格点,使它到A,B两点都占2个小方格答案不唯一;
(1)
解:如图,△ABC,BA=BC=;答案不唯一
(2)
解:如图△ABD,DA=DB=;答案不唯一
【点睛】
本题考查了作图-应用与设计作图,勾股定理,等腰三角形的性质和判定等知识,解题的关键是数形结合正确判定线段的长度.
19.(本题10分)(2022·福建·厦门一中九年级期中)已知关于x的一元二次方程.
(1)求证:无论m为何值,方程总有两个实数根;
(2)若方程只有一个根为正数,求m的取值范围.
【答案】(1)见解析
(2)m≤1
【解析】
【分析】
(1)根据根的判别式求出△的值,再进行判断即可;
(2)求得方程的解x1=1,x2=m-1,根据方程只有一个根为正数可得m-1≤0,求解即可.
(1)
证明:∵Δ=(-m)2-4×(m-1)
=m2-4m+4
=(m-2)2≥0,
∴无论m为何值,方程总有两个实数根;
(2)
解一元二次方程x2-mx+m-1=0得,x1=1,x2=m-1,
∵方程只有一个根为正数,则m-1≤0,解得m≤1.
故m的取值范围为m≤1.
【点睛】
本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2-4ac:当Δ>0,方程有两个不相等的实数根;当Δ=0,方程有两个相等的实数根;当Δ<0,方程没有实数根.
20.(本题10分)(2022·湖南·道县朝阳学校八年级阶段练习)如图,已知四边形ABCD是平行四边形,BE⊥AC,DF⊥AC,求证:BE=DF.
【答案】见解析
【解析】
【分析】
可证明△ABE≌△CDF,即可得到结论.
【详解】
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAC=∠DCA,
∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠DFC=90°,
在△ABE和△CDF中 ,
,
∴△ABE≌△CDF(AAS).
∴BE=DF.
【点睛】
此题考查平行四边形的性质和全等三角形的判定及性质,掌握平行四边形的性质和全等三角形的判定是解决问题的关键.
21.(本题12分)(2023·河南·三模)某学校开展防疫知识宣传教育活动,为了解这次活动的效果,学校从七、八年级现有各400名的学生中随机抽取学生进行调查,过程如下:
从七、八年级各随机抽取20名学生,进行防疫知识测试,测试成绩(百分制)如下:
七年级:85 79 89 83 89 98 68 89 79 59 99 87 85 89 97 86 89 90 89 77
八年级:71 94 87 92 55 94 98 78 86 94 62 99 94 51 88 97 94 98 85 91
(1)按如下频数分布表整理描述这两组样本数据.请补全七年级20名学生测试成绩的频数分布表;
(说明:成绩为90分及以上为优秀,80~89分为良好,80分以下为不合格)
(2)两组样本数据的平均数、中位数、众数优秀率如表所示,请补充完整;
(3)若八年级学生全部参加这次考试,试估计八年级成绩优秀的学生人数;
(4)整体成绩较好的年级为哪个?理由是什么?(至少从两个不同的角度说明合理性)
【答案】(1)3;4
(2)20%,91.5
(3)220人
(4)八年级的整体成绩较好,见解析
【解析】
【分析】
(1)根据七年级的20个数据数出成绩在69.5~79.5与89.5~100的人数填入表中;
(2)根据(1)题表中的七年级89.5~100的人数4与总人数20相除计算优秀率;把八年级的20名学生的成绩按从小到大的顺序排列,取第10个与第11个数的平均数;
(3)用八年级总人数400乘以八年级优秀率55%估计;
(4)根据平均数,中位数,众数八年级相对较好,说明八年级成绩总体较好.
(1)
由题意可得,频数分布表如下:
故答案为:3,4;
(2)
由题意可得,
七年级20名学生测试成绩的优秀率为: ,
将八年级20名学生的测试成绩按从小到大的顺序排列为:
51,55,62,71,78,85,86,87,88,91,92,94,94,94,94,94,97,98,98,99,
位于中间位置的两个数是 91,92,所以中位数是(91+92)÷2=91.5.
故答案为:20%,91.5;
(3)
(人),
答:估计八年级成绩优秀的学生人数有220人;
(4)
八年级的整体成绩较好,理由如下:
该校七、八年级中各随机抽取20名学生的测试成绩,八年级的平均数,中位数,众数以及优秀率均比七年级的大,所以八年级的整体成绩较好.
【点睛】
本题主要考查了平均数,中位数,众数的概念与计算,解决问题的关键是深刻理解概念,熟练计算。(1)题采用唱票统计;(2)题用人数4除以总人数20计算七年级优秀率;用八年级20名学生成绩从小到大的排列后第10个与第11个数的平均数;(3)题用八年级全部400乘以优秀率;(4)题比较两个年级段的平均数,中位数,众数,好者整体成绩较好.
22.(本题12分)(2023·山东泰安·三模)端午节临近,某商店推出白水粽和红豆粽,其中红豆粽的销售单价是白水粽的1.25倍,4月份,红豆粽和白水粽共销售150千克,红豆粽的销售额是1200元,白水粽的销售额为1440元.
(1)求红豆粽、白水粽的销售单价各是多少?
(2)为迎接端午节到来,该蛋糕店在5月推出“粽享会员”活动,对所有的粽子均可享受a%的折扣,非“粽享会员”需要按照原价购买,就红豆粽而言,5月销量比4月销量增加了a%,其中通过“粽享会员”购买的销量占5月红豆粽销量的,而5月红豆粽的销售总额比4月红豆粽销售额提高了a%,求a的值.
【答案】(1)红豆粽的销售单价是20元,白水粽的销售单价是16元
(2)a的值为10
【解析】
【分析】
(1)根据红豆粽销售重量+白水粽重量=150千克作为等关系列方程即可;
(2)根据5月红豆粽的销售总额比4月红豆粽销售额提高了112a%作为等量关系列方程.
(1)
设白水粽的销售单价是x元,则红豆粽的销售单价是1.25x元,
依题意得:150,
解得:x=16,
经检验,x=16是原方程的解,且符合题意,
∴1.25x=1.25×16=20.
答:红豆粽的销售单价是20元,白水粽的销售单价是16元.
(2)
红豆粽4月份的销量为1200÷20=60(千克).
依题意得:20×(1﹣a%)60(1+a%)+20×(1)×60(1+a%)=1200(1a%),
整理得:a2﹣10a=0,
解得:a1=10,a2=0(不合题意,舍去).
答:a的值为10.
【点睛】
本题考查列分式方程和一元二次方程解决实际问题,解决问题的关键是根据题意找出等量关系列方程.
23.(本题14分)(2023年河北省石家庄市中考数学一模试卷)如图,在边长为6的正方形ABCD中,点M为对角线BD上任意一点(可与B,D重合),将线段AM绕点A逆时针旋转90°得到线段AN,连接MN,设BM=x.
(1)求证:△ABM≌△ADN;
(2)当时,求MN的长;
(3)嘉淇同学在完成(1)后有个想法:“△ABM与△MND也会存在全等的情况”,请判断嘉淇的想法是否正确,请直接写出△ABM与△MND全等时x的值;若不正确,请说明理由.
【答案】(1)见解析
(2)MN的长为
(3)正确;当△ABM与△MND全等时
【解析】
【分析】
(1)由全等三角形的判定定理证得结论;
(2)由得:,,推导出是直角三角形,利用勾股定理求得的长度;
(3)正确,抓住全等特征分析出,得和是全等的等腰直角三角形,即可得出结论.
(1)
证明:在正方形中,,
由旋转的性质知:,
,
,
在和中,
,
;
(2)
解:是正方形的对角线,且,
,,
,
由得:,,
,
在中,;
(3)
解:正确;;
理由如下:
如图:
当,易得和是全等的等腰直角三角形,
,,
正方形中,,
,
,
四边形为矩形,
又,
矩形为正方形,
,
(全等传递性),
此时.
当与全等时.
【点睛】
本题考查了正方形的性质,全等的判定以及勾股定理等,掌握全等三角形的判定以及勾股定理的应用是解决问题的关键.
题号
一
二
三
总分
得分
评卷人
得分
一、单选题(共40分)
零件个数(个)
6
7
8
人数(人)
15
22
13
评卷人
得分
二、填空题(共20分)
评卷人
得分
三、解答题(共90分)
年级
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
七年级
1
1
11
八年级
2
1
2
4
11
年级
平均数
中位数
众数
优秀率
七年级
85.3
88
89
八年级
85.4
94
55%
年级
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
七年级
1
1
3
11
4
八年级
2
1
2
4
11
沪科版八年级数学下学期核心考点精讲精练 专题12 期中模拟(一)-【专题重点突破】(原卷版+解析): 这是一份沪科版八年级数学下学期核心考点精讲精练 专题12 期中模拟(一)-【专题重点突破】(原卷版+解析),共24页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
沪科版八年级数学下学期核心考点精讲精练 期末模拟(一)-【专题重点突破】(原卷版+解析): 这是一份沪科版八年级数学下学期核心考点精讲精练 期末模拟(一)-【专题重点突破】(原卷版+解析),共28页。
沪科版八年级数学下学期核心考点精讲精练 期末模拟(五)-【专题重点突破】(原卷版+解析): 这是一份沪科版八年级数学下学期核心考点精讲精练 期末模拟(五)-【专题重点突破】(原卷版+解析),共32页。












