福建省福州十九中、延安中学2023-2024学年八年级上学期期末数学试题

这是一份福建省福州十九中、延安中学2023-2024学年八年级上学期期末数学试题，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A．B．C．D．
2．经测算，一粒芝麻的质量约为0.00000201kg，那么数据0.00000201用科学记数法表示为（ ）
A．B．C．D．
3．下列二次根式中，是最简二次根式的是（ ）
A．B．C．D．
4．下列运算错误的是（ ）
A．B．C．D．
5．点关于y轴的对称点的坐标是（ ）
A．B．C．D．
6．下列命题的逆命题成立的是（ ）
A．全等三角形的对应角相等B．如果两个数相等，那么它们的绝对值相等
C．两直线平行，同位角相等D．对顶角相等
7．下列多项式相乘，能用平方差公式计算的是（ ）
A．B．
C．D．
8．如图，在框中解分式方程的4个步骤中，其中根据等式基本性质的有（ ）
A．①②B．②④C．①③D．③④
9．平行四边形ABCD中，，，若一边上的高为4，则该平行四边形的面积为（ ）
A．20B．16C．15D．12
10．数学家欧几里得利用如图验证了勾股定理．以的三条边为边长向外作正方形ABDE，正方形ACHI，正方形BCGF，连接CE．若，，则的面积为（ ）
A．40B．32C．24D．18
二、填空题：本题共6小题，每小题4分，共24分．
11．若二次根式有意义，则a的取值范围为______．
12．分解因式：______．
13．等腰三角形的一个底角度数是70°，则这个等腰三角形的顶角度数为______．
14．如图，在正方形网格，四边形ABCD的四个顶点都在格点上，则的度数为______．
15．已知，则的值为______．
16．如图，中，，，点D，E在边AC上，∠DBE=75°，若，，则DE长为______．
三、解答题：本题共9小题，共86分．
17．（每小题4分，本题满分8分）
计算：（1）（2）
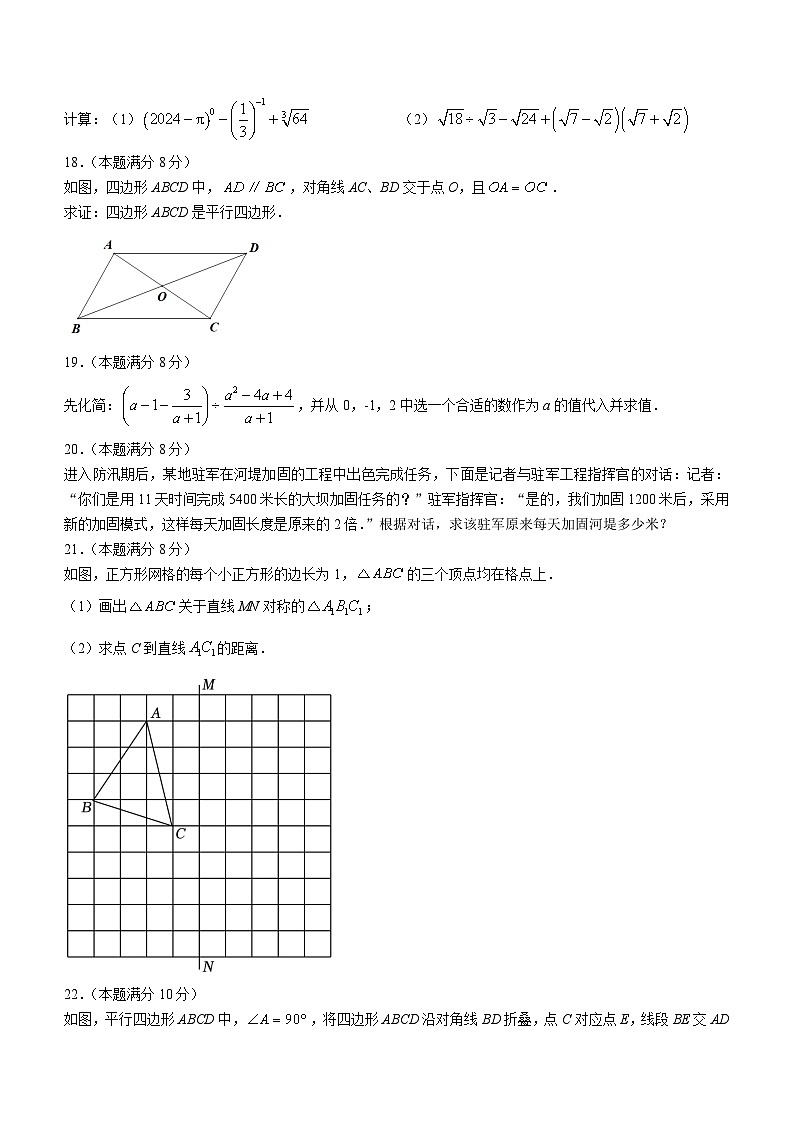
18．（本题满分8分）
如图，四边形ABCD中，，对角线AC、BD交于点O，且．
求证：四边形ABCD是平行四边形．
19．（本题满分8分）
先化简：，并从0，-1，2中选一个合适的数作为a的值代入并求值．
20．（本题满分8分）
进入防汛期后，某地驻军在河堤加固的工程中出色完成任务，下面是记者与驻军工程指挥官的对话：记者：“你们是用11天时间完成5400米长的大坝加固任务的？”驻军指挥官：“是的，我们加固1200米后，采用新的加固模式，这样每天加固长度是原来的2倍．”根据对话，求该驻军原来每天加固河堤多少米？
21．（本题满分8分）
如图，正方形网格的每个小正方形的边长为1，的三个顶点均在格点上．
（1）画出关于直线MN对称的；
（2）求点C到直线的距离．
22．（本题满分10分）
如图，平行四边形ABCD中，，将四边形ABCD沿对角线BD折叠，点C对应点E，线段BE交AD于点F．
（1）用尺规补全图形；
（2）若，，求BF．
23．（本题满分10分）
如图，是等腰直角三角形，，与关于AC对称，E为边AC上一点，连接BE并延长交CD于点F，作交BC于点G．
（1）求证：；
（2）探究：当为何值时，点G与点F关于AC对称．
24．（本题满分12分）
图1是一种长为a，宽为b的长方形，对角线长为c，将这样四个形状和大小完全相同的长方形拼成如图2所示的大正方形，设中间阴影部分的面积为．
（1）请用含a，b的代数式表示；
（2）若图2中的正方形面积ABCD面积为24，，求图1中长方形的周长；
（3）将7个这样的长方形按图3形式摆放，形成一个大长方形，设图中阴影部分的面积为，若，，求图1中长方形的面积．
25．（本题满分14分）
如图，在等边中，，CD为角平分线，点P为边AC上一点，连接PD．
（1）当P为AC中点时，求PD长；
（2）如图1，连接PB，求的最小值；
（3）如图2，过D点的直线l与∠ACB的边CA，CB分别交于点E，F，当直线l绕点D旋转时，是否为定值，若是，请求出该定值；若不是，请说明理由．
2023-2024学年第一学期八年级期末考
数学试题参考答案及评分标准
（1）本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可参照本答案的评分标准的精神进行评分．
（2）对解答题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的立意，可酌情给分．
（3）解答右端所注分数表示考生正确作完该步应得的累加分数．
（4）评分只给整数分，选择题和填空题均不给中间分．
一、选择题：（本大题有10小题，每小题4分，满分40分）
1．A；2．B；3．B；4．C；5．A；6．C；7．B；8．C；9．D；10．B．
二、填空题：（本大题有6小题，每小题4分，满分24分）
11．；12．；13．40°；14．45°；15．；16．．
三、解答题（本大题共9小题，共86分．请在答．题．卡．的相应位置作答）
17．（本题满分8分）
解：（1）
原式
（2）
原式
18．（本题满分8分）
（1）证明：∵，∴，
在与中，，
∴（AAS）
∴
∴四边形ABCD是平行四边形．
19．（本题满分8分）
解：（1）
由题意可得：，，∴，，
将代入得，原式
20．（本题满分8分）
解：设原来每天加固x米，
解这个方程得：
经检验是原方程的根
答：该地驻军原来每天加固300米．
21．（本题满分8分）
解：（1）如图，为所画图形．
（2）如图，连接
点C到直线的距离为
22．（本题满分10分）
（1）如图，即为所作图形．
（2）解：由折叠可知，
∵平行四边形ABCD，∴，
∴，∴，∴
设，则，∴
∵
在中，∴
∴
∴
∴．
23．（本题满分10分）
（1）证明：∵是等腰直角三角形，
∴，
由对称可知，
∴，∴
∵，∴，
∴
∴在与中
∴（AAS）
∴
（2）当时，G点与F点关于AC对称．
理由如下：连接GF
∵，∴
在中，
∵，∴
∴，∴
∵AC平分∠GCF，∴AC垂直平分GF
∴G点与F点关于AC对称．
24．（本题满分12分）
解：（1）
写成或都可得分．
（2）由勾股定理，
∴，∴
∴
∴
∴图1中长方形的周长为．
（3）根据题意，得
由
得
∴
答：图1中长方形的面积为14．
25．（本题满分14分）
解：（1）∵等边中，CD为角平分线，∴D为AB中点
图1
∵P为AC中点，∴DP为的中位线
∴．
（2）于H点
在与
，
∴
当时，PD有最小值，此时取得最小值．
∵，∴，∴
∴在中，
∴
的最小值为．
（3）解：作于M点，于N点，于Q点
∵CD为角平分线，∴
∴
∵CD为角平分线，∴
∵，∴
在中，
∴，∴
∵
∴
∴
∴
∴
∴为定值，且值为．解分式方程：．
解：…①
……②
…③
… ④