
备考2024届高考数学一轮复习讲义第四章三角函数第2讲同角三角函数的基本关系与诱导公式
展开1.同角三角函数的基本关系
(1)平方关系:sin2α+cs2α=1.
(2)商的关系:tan α=sinαcsα(α≠π2+kπ,k∈Z).
(3)公式常见变形:sin2α=1-cs2α;sinα=±1-cs2α;sin2α=sin2αsin2α+cs2α=tan2αtan2α+1,cs2α=cs2αsin2α+cs2α=① 1tan2α+1 ;(sinα±csα)2=1±2sinαcsα.
注意 利用平方关系时,若要开方,要注意判断符号.
2.诱导公式
1.[易错题]已知α是第二象限角,sinα=513,则csα=( A )
A.-1213B.-513C.513D.213
解析 因为α是第二象限角,所以csα<0,又sin2α+cs2α=1,所以csα=
-1-sin2α=-1213.
2.[2023贵州联考]已知tan θ=-2,则sinθ+csθsinθ=( D )
A.-1B.-3C.-12D.12
解析 因为tan θ=-2,则sinθ+csθsinθ=1+1tanθ=1-12=12.
3.[2023上饶重点中学模拟]下面诱导公式使用正确的是( C )
A.sin(θ-π2)=csθB.cs(3π2+θ)=-sinθ
C.sin(3π2-θ)=-csθD.cs(θ-π2)=-sinθ
解析 ∵sin(θ-π2)=-sin(π2-θ)=-csθ,∴A错误;∵cs(3π2+θ)=sinθ,∴B错误;∵sin(3π2-θ)=-csθ,∴C正确;∵cs(θ-π2)=cs(π2-θ)=sinθ,∴D错误.
4.sin 1 050°= -12 .
解析 sin 1 050°=sin(-30°)=-12.
5.[2023成都八中模拟]已知tan(π+α)=2,则sin(π2+α)+sin(π-α)cs(3π2+α)-2cs(π+α)= 34 .
解析 因为tan(π+α)=tan α=2,所以sin(π2+α)+sin(π-α)cs(3π2+α)-2cs(π+α)=csα+sinαsinα+2csα=1+tanαtanα+2=1+22+2=34.
研透高考 明确方向
命题点1 同角三角函数关系的应用
例1 (1)[2024山东模拟]若tan θ=2,则1+sinθcsθ=( B )
A.73B.75
C.54D.53
解析 易知csθ≠0,则1+sinθcsθ=1+sinθcsθ1=sin2θ+cs2θ+sinθcsθsin2θ+cs2θ=tan2θ+tanθ+1tan2θ+1=22+2+122+1=75.
(2)[2023全国卷乙]若θ∈(0,π2),tan θ=12,则sinθ-csθ= -55 .
解析 由tanθ=sinθcsθ=12,sin2θ+cs2θ=1,且θ∈(0,π2),解得sinθ=55,csθ=255,故sinθ-csθ=-55.
方法技巧
同角三角函数基本关系的应用技巧
(1)利用sin2α+cs2α=1和tan α=sinαcsα,可以解决sinα,csα,tan α的知一求二的问题,注意判断角的终边所在的象限.
(2)利用(sinα±csα)2=1±2sinαcsα,可以解决sinα+csα,sinαcsα,sinα-
cs α知一求二的问题,注意方程思想的应用.
(3)利用sin2α+cs2α=1可以实现角α的正、余弦互化;利用tan α=sinαcsα可以实现角α的弦、切互化,主要考查齐次式的使用技巧以及“1”的变形.
训练1 [多选/2023江西省上饶市第一中学模拟]已知θ∈(-π,0),sinθ+csθ=713,则下列结论正确的是( BD )
A.θ∈(-π,-π2)B.csθ=1213
C.tanθ=512D.sinθ-csθ=-1713
解析 由sinθ+csθ=713可得,csθ=713-sinθ,
则(713-sinθ)2+sin2θ=1,
解得sinθ=1213或sinθ=-513.
由θ∈(-π,0),可得sinθ=-513,csθ=1213,故B正确;
由sinθ=-513<0,csθ=1213>0可得θ为第四象限角,又θ∈(-π,0),所以θ∈
(-π2,0),故A错误;
tan θ=sinθcsθ=-512,故C错误;
sin θ-cs θ=-513-1213=-1713,故D正确.故选BD.
命题点2 诱导公式的应用
例2 (1)[全国卷Ⅲ]函数f(x)=15sin(x+π3)+cs(x-π6)的最大值为( A )
A.65B.1C.35D.15
解析 因为cs(x-π6)=cs[(x+π3)-π2]=sin(x+π3),所以f(x)=65sin(x+π3),所以f(x)的最大值为65,故选A.
(2)[北京高考]若函数f(x)=sin(x+φ)+csx的最大值为2,则常数φ的一个取值为 π2(答案不唯一) .
解析 易知当y=sin(x+φ),y=csx同时取得最大值1时,函数f(x)=sin(x+φ)+csx取得最大值2,故sin(x+φ)=csx,则φ=π2+2kπ,k∈Z,故常数φ的一个取值为π2.
方法技巧
应用诱导公式的一般思路
(1)化负角为正角,化大角为小角,直到化到锐角;
(2)统一角,统一名;
(3)角中含有π2的整数倍时,用公式去掉π2的整数倍.
训练2 (1)[2023山东省济宁市模拟]已知cs(π6-θ)=13,则cs(5π6+θ)+
2sin(5π3-θ)的值为 -1 .
解析 原式=cs[π-(π6-θ)]+2sin[3π2+(π6-θ)]=-cs(π6-θ)-2cs(π6-θ)=
-3cs(π6-θ)=-1.
(2)已知sinα是方程5x2-7x-6=0的根,且α是第三象限角,则sin(-α-3π2)cs(3π2-α)cs(π2-α)sin(π2+α)·
tan2(π-α)的值为 -916 .
解析 原式=-sin(3π2+α)cs(3π2-α)sinαcsα·tan2α=-csαsinαsinαcsα·tan2α=-tan2α.解方程5x2-7x-6=0,得x1=-35,x2=2.又α是第三象限角,∴sinα=-35,∴csα=-45,∴tan α=34.故原式=-tan2α=-916.
命题点3 同角三角函数基本关系与诱导公式的综合应用
例3 (1)[2023陕西模拟]已知0<α<π2,cs(α+π3)=-23,则tan (2π3-α)=( A )
A.52B.-52C.53D.-53
解析 由0<α<π2,得π3<α+π3<5π6,则sin(α+π3)=1-cs2(α+π3)=1-(-23)2=53,所以tan(α+π3)=sin(α+π3)cs(α+π3)=-52,所以tan(2π3-α)=tan[π-(α+π3)]=-tan(α+π3)=52.故选A.
(2)[全国卷Ⅰ]已知θ是第四象限角,且sin(θ+π4)=35,则tan(θ-π4)= -43 .
解析 解法一 因为sin(θ+π4)=35,所以cs(θ-π4)=sin[π2+(θ-π4)]=sin(θ+π4)=35.因为θ为第四象限角,所以-π2+2kπ<θ<2kπ,k∈Z,所以-3π4+2kπ<θ-π4<2kπ-π4,k∈Z,所以sin(θ-π4)=-1-(35)2=-45,所以tan(θ-π4)=sin(θ-π4)cs(θ-π4)=-43.
解法二 因为θ是第四象限角,且sin(θ+π4)=35,所以θ+π4为第一象限角,所以
cs(θ+π4)=45,所以tan(θ-π4)=sin(θ-π4)cs(θ-π4)=-cs[π2+(θ-π4)]sin[π2+(θ-π4)]=-cs(θ+π4)sin(θ+π4)=-43.
方法技巧
利用同角三角函数基本关系与诱导公式解题的基本思路
(1)分析结构特点,寻求条件及所求间的关系,尤其是角之间的关系;
(2)选择恰当公式,利用公式灵活变形;
(3)化简求值.
注意 (1)角的范围会影响三角函数值的符号,开方时要先判断三角函数值的符号.
(2)化简过程是恒等变换.
训练3 [2024安徽省皖江名校联考]已知在平面直角坐标系中,点M(2,4)在角α终边上,则sin3(π-α)+cs3(-α)sin3α-2cs3α=( B )
A.23B.32C.-35D.-53
解析 由题意可得tan α=2,所以原式=sin3α+cs3αsin3α-2cs3α=tan3α+1tan3α-2=8+18-2=32.故选B.课标要求
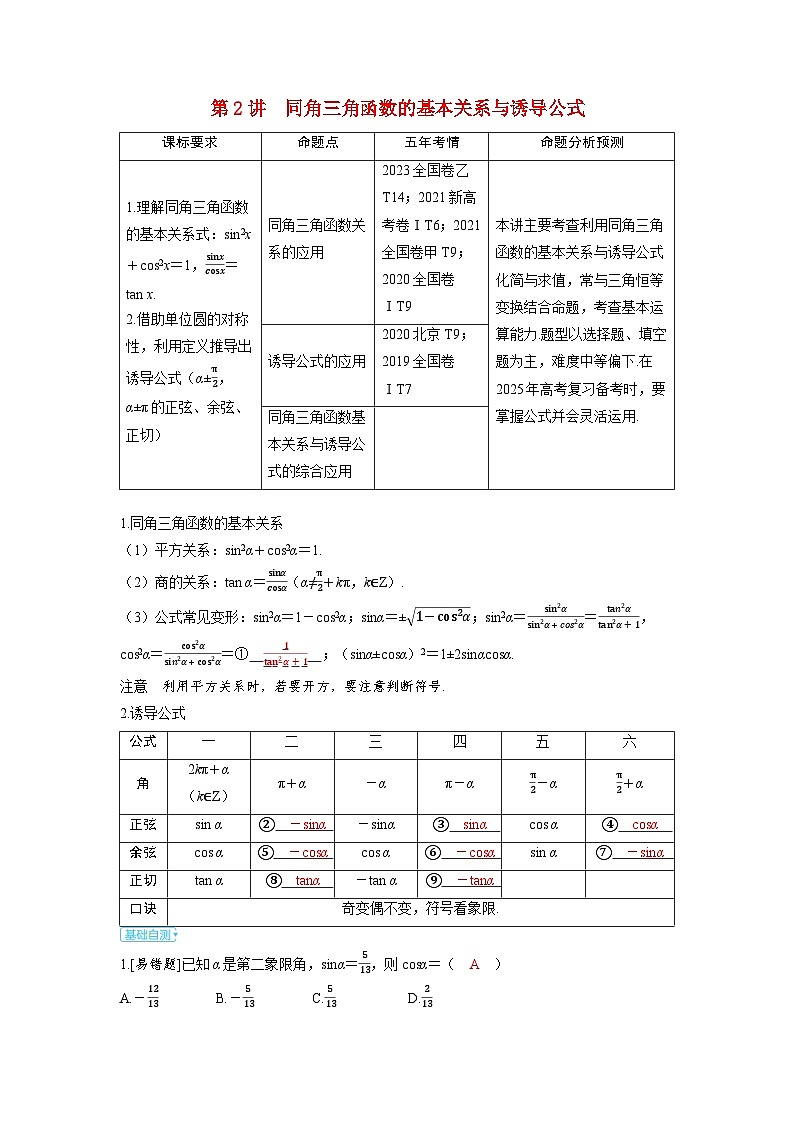
命题点
五年考情
命题分析预测
1.理解同角三角函数的基本关系式:sin2x+cs2x=1,sinxcsx=tan x.
2.借助单位圆的对称性,利用定义推导出诱导公式(α±π2,α±π的正弦、余弦、正切)
同角三角函数关系的应用
2023全国卷乙T14;2021新高考卷ⅠT6;2021全国卷甲T9;2020全国卷ⅠT9
本讲主要考查利用同角三角函数的基本关系与诱导公式化简与求值,常与三角恒等变换结合命题,考查基本运算能力.题型以选择题、填空题为主,难度中等偏下.在2025年高考复习备考时,要掌握公式并会灵活运用.
诱导公式的应用
2020北京T9;2019全国卷ⅠT7
同角三角函数基本关系与诱导公式的综合应用
公式
一
二
三
四
五
六
角
2kπ+α(k∈Z)
π+α
-α
π-α
π2-α
π2+α
正弦
sin α
② -sinα
-sinα
③ sinα
cs α
④ csα
余弦
cs α
⑤ -csα
cs α
⑥ -csα
sin α
⑦ -sinα
正切
tan α
⑧ tanα
-tan α
⑨ -tanα
口诀
奇变偶不变,符号看象限.
2024届高考数学一轮复习第4章第2节同角三角函数的基本关系与诱导公式学案: 这是一份2024届高考数学一轮复习第4章第2节同角三角函数的基本关系与诱导公式学案,共18页。学案主要包含了教材概念·结论·性质重现,基本技能·思想·活动经验等内容,欢迎下载使用。
高考数学一轮复习第4章第2节同角三角函数的基本关系与诱导公式学案: 这是一份高考数学一轮复习第4章第2节同角三角函数的基本关系与诱导公式学案,共12页。学案主要包含了教材概念·结论·性质重现,基本技能·思想·活动经验等内容,欢迎下载使用。
高考数学统考一轮复习第4章4.2同角三角函数的基本关系及诱导公式学案: 这是一份高考数学统考一轮复习第4章4.2同角三角函数的基本关系及诱导公式学案,共9页。学案主要包含了知识重温,小题热身等内容,欢迎下载使用。












