2023-2024学年江苏省南京五中学九上数学期末达标检测试题含答案

这是一份2023-2024学年江苏省南京五中学九上数学期末达标检测试题含答案，共8页。试卷主要包含了两个相似三角形，其面积比为16，若点A，关于二次函数y=﹣等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题（每题4分，共48分）
1．如图，从一块半径为的圆形铁皮上剪出一个圆心角是的扇形，则此扇形围成的圆锥的侧面积为（ ）

A．B．C．D．
2．如图所示的几何体是由个大小相同的小立方块搭成，它的俯视图是（ ）
A．B．C．D．
3．下列命题正确的是( )
A．圆是轴对称图形，任何一条直径都是它的对称轴
B．平分弦的直径垂直于弦，并且平分弦所对的弧
C．相等的圆心角所对的弧相等，所对的弦相等
D．同弧或等弧所对的圆周角相等
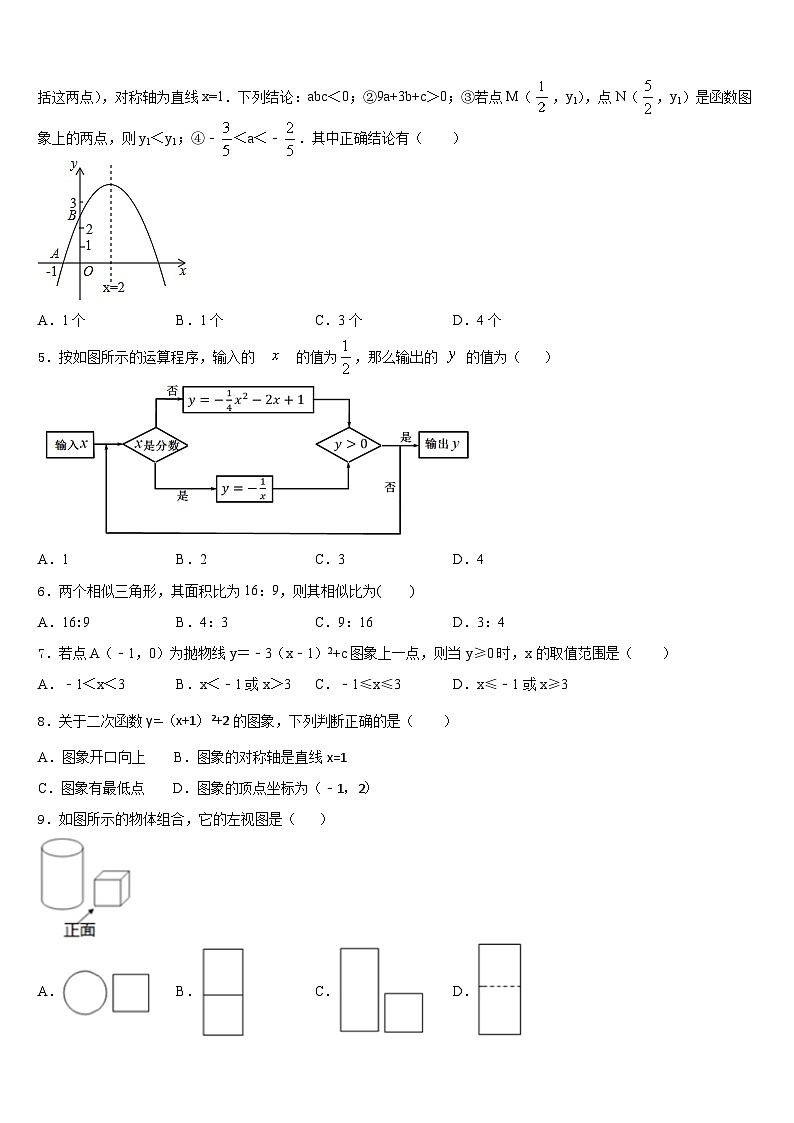
4．如图，二次函数y=ax1+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，1）与（0，3）之间（不包括这两点），对称轴为直线x=1．下列结论：abc＜0；②9a+3b+c＞0；③若点M（，y1），点N（，y1）是函数图象上的两点，则y1＜y1；④﹣＜a＜﹣．其中正确结论有（ ）
A．1个B．1个C．3个D．4个
5．按如图所示的运算程序，输入的 的值为，那么输出的 的值为（ ）
A．1B．2C．3D．4
6．两个相似三角形，其面积比为16：9，则其相似比为( )
A．16:9B．4：3C．9：16D．3：4
7．若点A（﹣1，0）为抛物线y＝﹣3（x﹣1）2+c图象上一点，则当y≥0时，x的取值范围是（ ）
A．﹣1＜x＜3B．x＜﹣1或x＞3C．﹣1≤x≤3D．x≤﹣1或x≥3
8．关于二次函数y=﹣（x+1）2+2的图象，下列判断正确的是（ ）
A．图象开口向上 B．图象的对称轴是直线x=1
C．图象有最低点 D．图象的顶点坐标为（﹣1，2）
9．如图所示的物体组合，它的左视图是（ ）
A．B．C．D．
10．如图，△ABC中，点D，E在边AB，AC上，DE∥BC，△ADE与△ABC的周长比为2∶5，则AD∶DB为( )
A．2∶5B．4∶25C．2∶3D．5∶2
11．用频率估计概率，可以发现，某种幼树在一定条件下移植成活的概率为0.9，下列说法正确的是（ ）
A．种植10棵幼树，结果一定是“有9棵幼树成活”
B．种植100棵幼树，结果一定是“90棵幼树成活”和“10棵幼树不成活”
C．种植10n棵幼树，恰好有“n棵幼树不成活”
D．种植n棵幼树，当n越来越大时，种植成活幼树的频率会越来越稳定于0.9
12．若反比例函数y=图象经过点（5，-1），该函数图象在（ ）
A．第一、二象限B．第一、三象限C．第二、三象限D．第二、四象限
二、填空题（每题4分，共24分）
13．如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG，点F，G分别在AD，BC上，连结OG，DG，若OG⊥DG，且⊙O的半径长为1，则BC+AB的值______．
14．如图，直角三角形的直角顶点在坐标原点，，若点在反比例函数的图象上，则经过点的反比例函数解析式为___；
15．袋子中有10个除颜色外完全相同的小球在看不到球的条件下，随机地从袋中摸出一个球，记录颜色后放回，将球摇匀重复上述过程1500次后，共到红球300次，由此可以估计袋子中的红球个数是_____．
16．点A（-1，m）和点B（-2，n）都在抛物线上，则m与n的大小关系为m______n（填“”或“”）．
17．如图，矩形ABCD绕点A旋转90°，得矩形，若三点在同一直线上，则的值为_______________
18．若关于x的一元二次方程有两个相等的实数根，则m的值为_________．
三、解答题（共78分）
19．（8分）阅读材料：求解一元一次方程，需要根据等式的基本性质，把方程转化为的形式；求解二元一次方程组，需要通过消元把它转化为一元一次方程来解；求解三元一次方程组，要把它转化为二元一次方程组来解；求解一元二次方程，需要把它转化为连个一元一次方程来解；求解分式方程，需要通过去分母把它转化为整式方程来解；各类方程的解法不尽相同，但是它们都用到一种共同的基本数学思想——转化，即把未知转化为已知来求解.
用“转化”的数学思想，我们还可以解一些新的方程.
例如，解一元三次方程，通过因式分解把它转化为，通过解方程和，可得原方程的解.
再例如，解根号下含有来知数的方程：，通过两边同时平方把它转化为，解得：. 因为，且，所以不是原方程的根，是原方程的解.
（1）问题：方程的解是，__________，__________；
（2）拓展：求方程的解.
20．（8分）如图，在边长为的正方形中，点是射线上一动点(点不与点重合)，连接，点是线段上一点，且，连接.
求证:；
求证:；
直接写出的最小值.
21．（8分）如图，与交于点，过点，交与点，交与点F，，，，.
(1)求证：
(2)若，求证：
22．（10分）如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，
（1）求证：AC2＝AB•AD；
（2）求证：△AFD∽△CFE．
23．（10分）如图，在Rt△ABC中，∠ABC=90°，以AB为直径作⊙O，点D为⊙O上一点，且CD=CB，连接DO并延长交CB的延长线于点E，连接OC．
(1) 判断直线CD与⊙O的位置关系，并说明理由；
(2) 若BE=，DE=3，求⊙O的半径及AC的长．
24．（10分）关于x的一元二次方程有两个不相等的实数根．
（1）求m的取值范围；
（2）若，是一元二次方程的两个根，且，求m的值．
25．（12分）如图，抛物线y＝－x2＋bx＋c与x轴交于点A（－1，0），与y轴交于点B（0，2），直线y＝x－1与y轴交于点C，与x轴交于点D，点P是线段CD上方的抛物线上一动点，过点P作PF垂直x轴于点F，交直线CD于点E，
（1）求抛物线的解析式；
（2）设点P的横坐标为m，当线段PE的长取最大值时，解答以下问题．
①求此时m的值．
②设Q是平面直角坐标系内一点，是否存在以P、Q、C、D为顶点的平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
26．（12分）某商品的进价为每件50元，售价为每件60元，每个月可卖出200件．如果每
件商品的售价上涨1元，则每个月少卖10件（每件售价不能高于72元）．设每件商品的售价上涨x元（x
为整数），每个月的销售利润为y元，
（1）求y与x的函数关系式，并直接写出x的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大月利润是多少元？
参考答案
一、选择题（每题4分，共48分）
1、A
2、C
3、D
4、D
5、D
6、B
7、C
8、D
9、D
10、C
11、D
12、D
二、填空题（每题4分，共24分）
13、4+
14、
15、2
16、＜.
17、
18、0
三、解答题（共78分）
19、（1）；（2）
20、（1）证明见解析；（2）证明见解析；（3）的最小值为
21、（1）见解析；（2）见解析
22、（1）证明见解析；（2）证明见解析.
23、（1）DC是⊙O的切线，理由见解析；（2）半径为1，AC=
24、（1）m＜；（2）﹣1．
25、（1）y＝﹣x1+x+1；（1）①m＝；②存在以P、Q、C、D为顶点的四边形是平行四边形，点Q的坐标为
26、（1）y=－10x2＋100x＋1，0＜x≤2（2）每件商品的售价定为5元时，每个月可获得最大利润，最大月利润是3元