贵州省剑河县2023-2024学年九年级数学第一学期期末联考模拟试题含答案

这是一份贵州省剑河县2023-2024学年九年级数学第一学期期末联考模拟试题含答案，共8页。试卷主要包含了已知二次函数，有一则笑话等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项：
1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3．考试结束后，将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．如图，已知等边的边长为，以为直径的圆交于点，以为圆心，为半径作圆，是上一动点，是的中点，当最大时，的长为（ ）
A．B．C．D．
2．二次函数y=(x+2)2-3的顶点坐标是（ ）
A．(﹣2，3)B．(2，3)C．(﹣2，﹣3)D．(2，﹣3)
3．在同一直角坐标系中，函数y=kx2﹣k和y=kx+k（k≠0）的图象大致是（ ）
A．B．C．D．
4．已知二次函数（a≠0）的图象如图所示，则下列结论：①b＜0，c＞0；②a+b+c＜0；③方程的两根之和大于0；④a﹣b+c＜0，其中正确的个数是（ ）
A．4个B．3个C．2个D．1个
5．在反比例函数y＝的图象上有两点A（x1，y1），B（x2，y2），当0＞x1＞x2时，有y1＞y2，则k的取值范围是（ ）
A．k≤B．k
6．二次函数y=a+bx+c的图象如图所示，则下列关系式错误的是（ ）
A．a＜0B．b＞0C．﹣4ac＞0D．a+b+c＜0
7．如图，⊙C过原点，与x轴、y轴分别交于A、D两点．已知∠OBA=30°，点D的坐标为（0，2），则⊙C半径是（ ）
A．B．C．D．2
8．若反比例函数的图像经过点，则下列各点在该函数图像上的为（ ）
A．B．C．D．
9．有一则笑话：妈妈正在给一对双胞胎洗澡，先洗哥哥，再洗弟弟．刚把两人洗完，就听到两个小家伙在床上笑．“你们笑什么？”妈妈问．“妈妈！”老大回答，“您给弟弟洗了两回，可是还没给我洗呢！”此事件发生的概率为( )
A．B．C．D．1
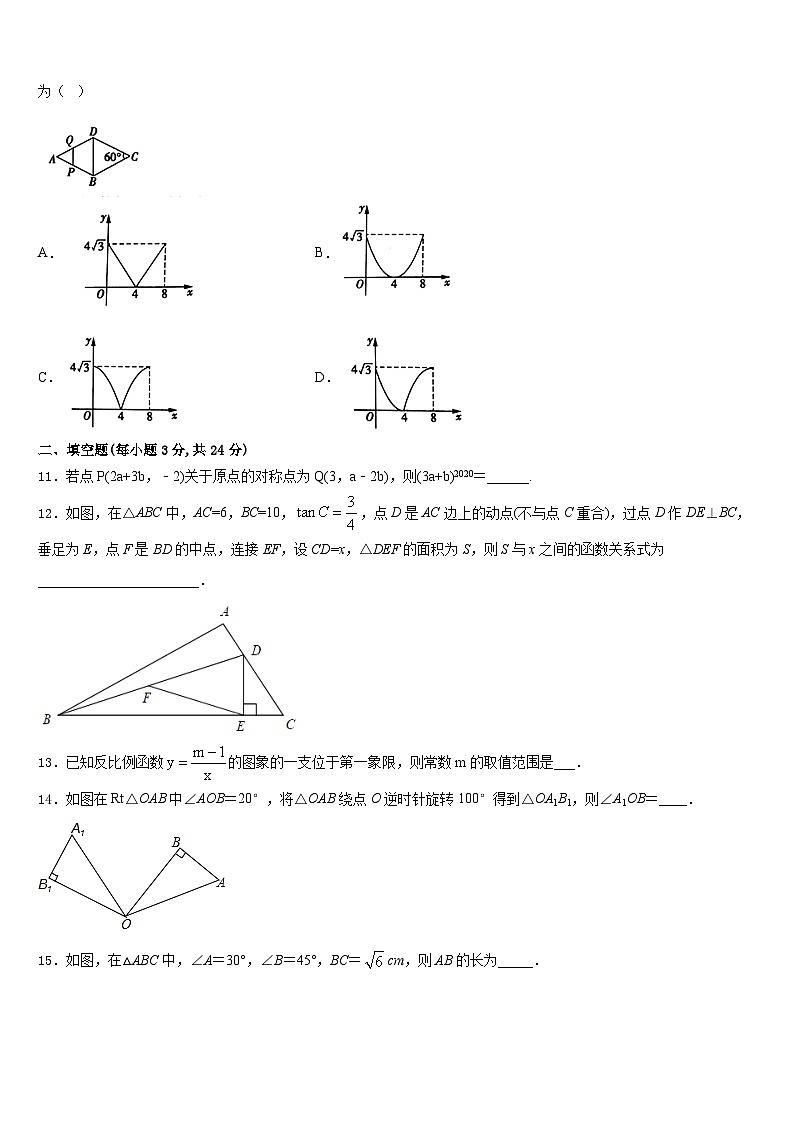
10．如图，菱形的边长是，动点同时从点出发，以的速度分别沿运动，设运动时间为，四边形的面积为，则与的函数关系图象大致为（ ）
A．B．
C．D．
二、填空题(每小题3分,共24分)
11．若点P(2a+3b，﹣2)关于原点的对称点为Q(3，a﹣2b)，则(3a+b)2020＝______.
12．如图，在△ABC中，AC=6，BC=10，，点D是AC边上的动点(不与点C重合)，过点D作DE⊥BC，垂足为E，点F是BD的中点，连接EF，设CD=x，△DEF的面积为S，则S与x之间的函数关系式为_______________________．
13．已知反比例函数的图象的一支位于第一象限，则常数m的取值范围是___．
14．如图在Rt△OAB中∠AOB＝20°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB＝____．
15．如图，在△ABC中，∠A＝30°，∠B＝45°，BC＝cm，则AB的长为_____．
16．小勇第一次抛一枚质地均匀的硬币时正面向上,他第二次再抛这枚硬币时,正面向
上的概率是 .
17．一个不透明的布袋中装有3个白球和5个红球，它们除了颜色不同外，其余均相同，从中随机摸出一个球，摸到红球的概率是______.
18．把抛物线y=2x2先向下平移1个单位，再向左平移2个单位，得到的抛物线的解析式是_______.
三、解答题(共66分)
19．（10分）国内猪肉价格不断上涨，已知今年10月的猪肉价格比今年年初上涨了80%，李奶奶10月在某超市购买1千克猪肉花了72元钱．
（1）今年年初猪肉的价格为每千克多少元？
（2）某超市将进货价为每千克55元的猪肉按10月价格出售，平均一天能销售出100千克，随着国家对猪肉价格的调控，超市发现猪肉的售价每千克下降1元，其日销售量就增加10千克，超市为了实现销售猪肉每天有1800元的利润，并且尽可能让顾客得到实惠，猪肉的售价应该下降多少元？
20．（6分）问题呈现：
如图 1，在边长为 1 小的正方形网格中，连接格点 A、B 和 C、D，AB 和 CD 相交于点 P，求 tan ∠CPB 的值方法归纳：求一个锐角的三角函数值，我们往往需要找出(或构造出)一个直角三角形，观察发现问题中∠ CPB不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题，比如连接格点 B、 E，可得 BE∥CD，则∠ABE=∠CPB，连接AE，那么∠CPB 就变换到 Rt△ABE 中．问题解决：
（1）直接写出图 1 中 tan CPB 的值为______；
（2）如图 2，在边长为 1 的正方形网格中，AB 与 CD 相交于点 P，求 cs CPB 的值．
21．（6分）甲、乙两名同学玩一个游戏：在一个不透明的口袋中装有标号分别为1，2，3，4的四个小球(除标号外无其它差异).从口袋中随机摸出一个小球，记下标号后放回口袋中，充分摇匀后，再从口袋中随机摸出一个小球，记下该小球的标号，两次记下的标号分别用x、y表示.若x＋y为奇数，则甲获胜；若x＋y为偶数，则乙获胜.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法，求(x，y)所有可能出现的结果总数；
(2)你认为这个游戏对双方公平吗？请说明理由.
22．（8分）（问题情境）
（1）古希腊著名数学家欧几里得在《几何原本》提出了射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项．射影定理是数学图形计算的重要定理．其符号语言是：如图1，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，则：（1）AC²=AB·AD；(2)BC²=AB·BD；(3)CD² = AD·BD；请你证明定理中的结论（1）AC² = AB·AD．
（结论运用）
（2）如图2，正方形ABCD的边长为3，点O是对角线AC、BD的交点，点E在CD上，过点C作CF⊥BE，垂足为F，连接OF，
①求证：△BOF∽△BED；
②若，求OF的长．
23．（8分）根据2019年莆田市初中毕业升学体育考试内容要求，甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练，三名学生随机选择其中的一场地进行训练．
（1）用列表法或树形图表示出的所用可能出现的结果；
（2）求甲、乙、丙三名学生在同一场地进行训练的概率；
（3）求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率．
24．（8分）在等腰直角三角形中，，，点在斜边上（），作，且，连接，如图（1）．
（1）求证：；
（2）延长至点，使得，与交于点．如图（2）．
①求证：；
②求证：．

25．（10分）如图，已知抛物线经过点、，且与轴交于点，抛物线的顶点为，连接，点是线段上的一个动点（不与、）重合.
（1）求抛物线的解析式，并写出顶点的坐标；
（2）过点作轴于点，求面积的最大值及取得最大值时点的坐标；
（3）在（2）的条件下，若点是轴上一动点，点是抛物线上一动点，试判断是否存在这样的点，使得以点，，，为顶点的四边形是平行四边若存在，请直接写出点的坐标：若不存在，请说明理由.
26．（10分）如图，一次函数y＝kx＋b与反比例函数y＝的图象在第一象限交于A，B两点，B点的坐标为(3，2)，连接OA，OB，过B作BD⊥y轴，垂足为D，交OA于C，若OC＝CA．
(1)求一次函数和反比例函数的表达式；
(2)求△AOB的面积．
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、D
4、B
5、D
6、D
7、B
8、C
9、A
10、C
二、填空题(每小题3分,共24分)
11、1
12、
13、m＞1
14、80°．
15、
16、
17、
18、y＝2（x＋2）2﹣1
三、解答题(共66分)
19、（1）每千克40元（2）猪肉的售价应该下降5元
20、（1）2；（2）
21、 (1)见解析；(2)这个游戏对双方公平，理由见解析.
22、（1）见解析；（2）①见解析；②
23、（1）共有8种可能；（2）；（3）
24、（1）见解析；（1）①见解析；②见解析
25、（1），D的坐标为（1，4）；（2）当m=时 △BPE的面积取得最大值为，P的坐标是（，3）；（3）存在，M点的坐标为；；；；；
26、 (1) y＝；y＝－x＋6(2)