福建省厦门市第六中学2023-2024学年数学九年级第一学期期末考试模拟试题含答案

这是一份福建省厦门市第六中学2023-2024学年数学九年级第一学期期末考试模拟试题含答案，共9页。试卷主要包含了平移抛物线y＝﹣，方程的解是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
1．如图，一个直角梯形的堤坝坡长AB为6米，斜坡AB的坡角为60°，为了改善堤坝的稳固性，准备将其坡角改为45°，则调整后的斜坡AE的长度为（ ）
A．3米B．3米C．（3﹣2）米D．（3﹣3）米
2．如图，在Rt△ABC中，∠ABC=90°，tan∠BAC=2，A（0，a），B（b，0），点C在第二象限，BC与y轴交于点D（0，c），若y轴平分∠BAC，则点C的坐标不能表示为（ ）
A．（b+2a，2b）B．（﹣b﹣2c，2b）
C．（﹣b﹣c，﹣2a﹣2c）D．（a﹣c，﹣2a﹣2c）
3．甲袋中装有形状、大小与质地都相同的红球3个，乙袋中装有形状、大小与质地都相同的红球2个，黄球1个，下列事件为随机事件的是（ ）
A．从甲袋中随机摸出1个球，是黄球
B．从甲袋中随机摸出1个球，是红球
C．从乙袋中随机摸出1个球，是红球或黄球
D．从乙袋中随机摸出1个球，是黄球
4．平移抛物线y＝﹣（x﹣1）（x+3），下列哪种平移方法不能使平移后的抛物线经过原点（ ）
A．向左平移1个单位B．向上平移3个单位
C．向右平移3个单位D．向下平移3个单位
5．为了估计水塘中的鱼数，养鱼者先从鱼塘中捕获30条鱼，在每一条鱼身上做好标记后把这些鱼放归鱼塘，再从鱼塘中打捞鱼。通过多次实验后发现捕捞的鱼中有作记号的频率稳定在2.5%左右，则鱼塘中鱼的条数估计为（ ）
A．600条B．1200条C．2200条D．3000条
6．在Rt△ABC中，∠C = 90°，∠A、∠B、∠C所对的边分别为a、b、c，下列等式中成立的是（ ）
A．B．C．D．
7．如图，已知⊙O的半径为13，弦AB长为24，则点O到AB的距离是( )
A．6B．5C．4D．3
8．在平面直角坐标系中，对于二次函数，下列说法中错误的是（ ）
A．的最小值为1
B．图象顶点坐标为，对称轴为直线
C．当时，的值随值的增大而增大，当时，的值随值的增大而减小
D．当时，的值随值的增大而减小，当时，的值随值的增大而增大
9．在△ABC与△DEF中，，，如果∠B=50°，那么∠E的度数是（ ）．
A．50°；B．60°；
C．70°；D．80°．
10．方程的解是（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
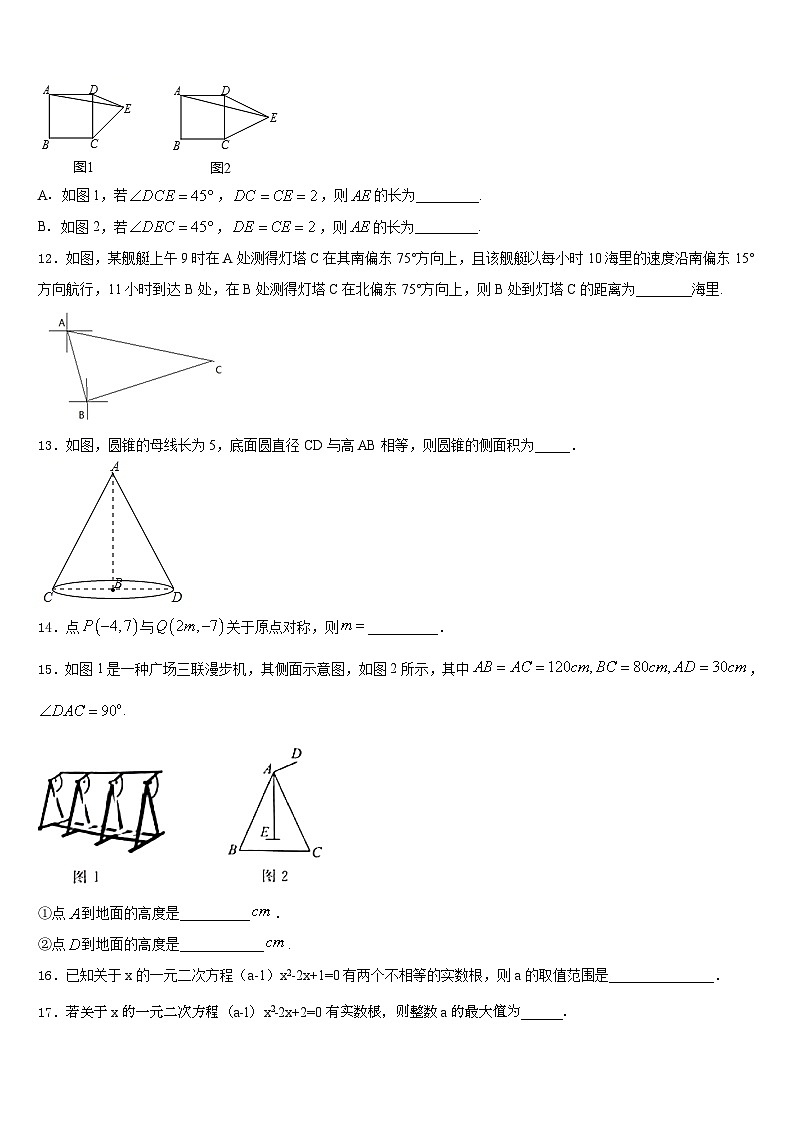
11．已知点是正方形外的一点，连接，，.请从下面A，B两题中任选一题作答.我选择_______题:
A．如图1，若，，则的长为_________.
B．如图2，若，，则的长为_________.
12．如图，某舰艇上午9时在A处测得灯塔C在其南偏东75°方向上，且该舰艇以每小时10海里的速度沿南偏东15°方向航行，11小时到达B处，在B处测得灯塔C在北偏东75°方向上，则B处到灯塔C的距离为________海里.
13．如图，圆锥的母线长为5，底面圆直径CD与高AB相等，则圆锥的侧面积为_____．
14．点与关于原点对称，则__________．
15．如图1是一种广场三联漫步机，其侧面示意图，如图2所示，其中，.
①点到地面的高度是__________．
②点到地面的高度是____________.
16．已知关于x的一元二次方程（a-1）x2-2x+1=0有两个不相等的实数根，则a的取值范围是_______________．
17．若关于x的一元二次方程（a﹣1）x2﹣2x+2=0有实数根，则整数a的最大值为______．
18．在一个不透明的盒子中装有12个白球，若干个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球是白球的概率是，则黄球个数为__________．
三、解答题(共66分)
19．（10分）计算：
（1）tan60°-+(3.14-π)0;
（2）解方程：．
20．（6分）如图所示是某一蓄水池每小时的排水量V（m3/h）与排完水池中的水所用的时间t（h）之间的函数关系图象．
（1）请你根据图象提供的信息求出此蓄水池的总蓄水量；
（2）写出此函数的解析式；
（3）若要6 h排完水池中的水，那么每小时的排水量应该是多少？
21．（6分）已知抛物线，求证:无论为何值，抛物线与轴总有两个交点.
22．（8分）（1）（学习心得）于彤同学在学习完“圆”这一章内容后，感觉到一些几何问题如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易.例如：如图1，在中，,是外一点，且,求的度数.若以点为圆心，为半径作辅助，则、必在上，是的圆心角，而是圆周角，从而可容易得到=________.
（2）（问题解决）如图2，在四边形中，,,求的度数.
（3）（问题拓展）如图3，是正方形的边上两个动点，满足.连接交于点，连接交于点,连接交于点,若正方形的边长为2，则线段长度的最小值是_______.
23．（8分）如图，抛物线过点和，点为线段上一个动点(点与点不重合)，过点作垂直于轴的直线与直线和抛物线分别交于点．
（1）求此抛物线的解析式；
（2）若点是的中点，则求点的坐标；
（3）若以点为顶点的三角形与相似，请直接写出点的坐标．
24．（8分）数学兴趣小组对矩形面积为9，其周长m的范围进行了探究．兴趣小组的同学们已经能用“代数”的方法解决，以下是他们从“图形”的角度进行探究的部分过程，请把过程补充完整．
（1）建立函数模型．
设矩形相邻两边的长分别为x，y，由矩形的面积为9，得xy＝9，即y＝；由周长为m，得2（x+y）＝m，即y＝﹣x+．满足要求的（x，y）应是两个函数图象在第 象限内交点的坐标．
（2）画出函数图象．
函数y＝（x＞0）的图象如图所示，而函数y＝﹣x+的图象可由直线y＝﹣x平移得到，请在同一直角坐标系中画出直线y＝﹣x．
（3）平移直线y＝﹣x，观察函数图象．
①当直线平移到与函数y＝（x＞0）的图象有唯一交点（3，3）时，周长m的值为 ；
②在直线平移过程中，直线与函数y＝（x＞0）的图象交点个数还有哪些情况？请写出交点个数及对应的周长m的取值范围．
（4）得出结论
面积为9的矩形，它的周长m的取值范围为 ．
25．（10分）列一元二次方程解应用题
某公司今年1月份的纯利润是20万元，由于改进技术，生产成本逐月下降，3月份的纯利润是22.05万元．假设该公司2、3、4月每个月增长的利润率相同．
（1）求每个月增长的利润率；
（2）请你预测4月份该公司的纯利润是多少？
26．（10分）在，，．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．
（1）观察猜想
如图1，当时，的值是 ，直线BD与直线CP相交所成的较小角的度数是 ．
（2）类比探究
如图2，当时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．
（3）解决问题
当时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．
参考答案
一、选择题(每小题3分,共30分)
1、A
2、C
3、D
4、B
5、B
6、B
7、B
8、C
9、C
10、B
二、填空题(每小题3分,共24分)
11、A或B
12、20
13、5π
14、
15、
16、a＜2且a≠1．
17、1
18、24
三、解答题(共66分)
19、（1）2；（2) x1=2，x2=1．
20、（1）48000 m3（2）V= （3）8000 m3
21、证明见解析
22、（1）45；（2）25°；（3）
23、（1）；（2）；（3）P(,)或P(,)
24、（1）一；（2）见解析；（3）①1；②0个交点时，m＜1；1个交点时，m＝1； 2个交点时，m＞1；（4）m≥1．
25、（1）每个月增长的利润率为5%．（2）4月份该公司的纯利润为23.1525万元．
26、（1）1，（2）45°（3），