山东省莱芜市2023-2024学年数学九年级第一学期期末教学质量检测试题含答案

这是一份山东省莱芜市2023-2024学年数学九年级第一学期期末教学质量检测试题含答案，共9页。试卷主要包含了下列说法正确的是，27的立方根是，如图所示的几何体，它的俯视图是等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
1．若关于的一元二次方程有一个根为0，则的值（ ）
A．0B．1或2C．1D．2
2．已知，则的值是（ ）
A．B．C．D．
3．下列说法正确的是（ ）
A．不可能事件发生的概率为;
B．随机事件发生的概率为
C．概率很小的事件不可能发生；
D．投掷一枚质地均匀的硬币次，正面朝上的次数一定是次
4．从甲、乙、丙、丁四人中选一人参加诗词大会比赛，经过三轮初赛，他们的平均成绩都是86分，方差如下表，你认为派谁去参赛更合适（ ）
A．甲B．乙C．丙D．丁
5．27的立方根是（ ）
A．±3B．±3C．3D．3
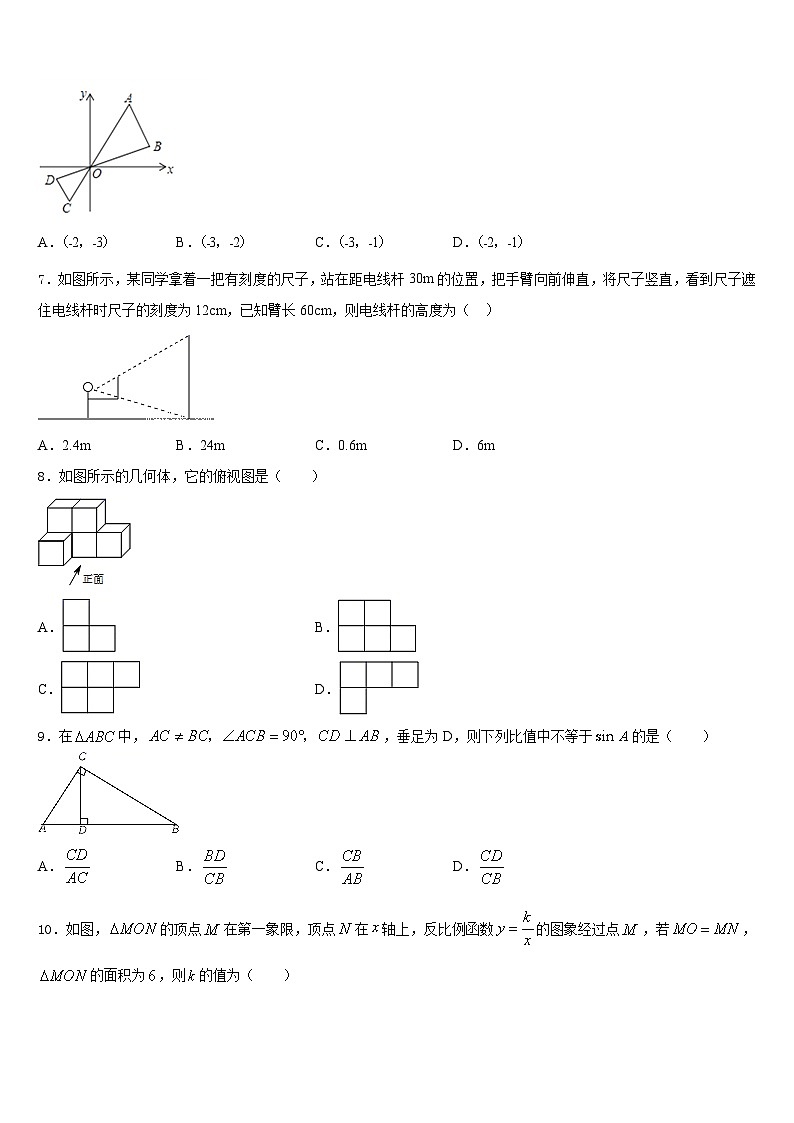
6．如图，线段AB两个端点坐标分别为A（4，6），B（6，2），以原点O为位似中心，在第三象限内将线段AB缩小为原来的后，得到线段CD，则点C的坐标为（ ）
A．（﹣2，﹣3）B．（﹣3，﹣2）C．（﹣3，﹣1）D．（﹣2，﹣1）
7．如图所示，某同学拿着一把有刻度的尺子，站在距电线杆30m的位置，把手臂向前伸直，将尺子竖直，看到尺子遮住电线杆时尺子的刻度为12cm，已知臂长60cm，则电线杆的高度为（ ）
A．2.4mB．24mC．0.6mD．6m
8．如图所示的几何体，它的俯视图是（ ）
A．B．
C．D．
9．在中，，垂足为D，则下列比值中不等于的是（ ）
A．B．C．D．
10．如图，的顶点在第一象限，顶点在轴上，反比例函数的图象经过点，若，的面积为，则的值为（ ）
A．B．C．D．
二、填空题(每小题3分,共24分)
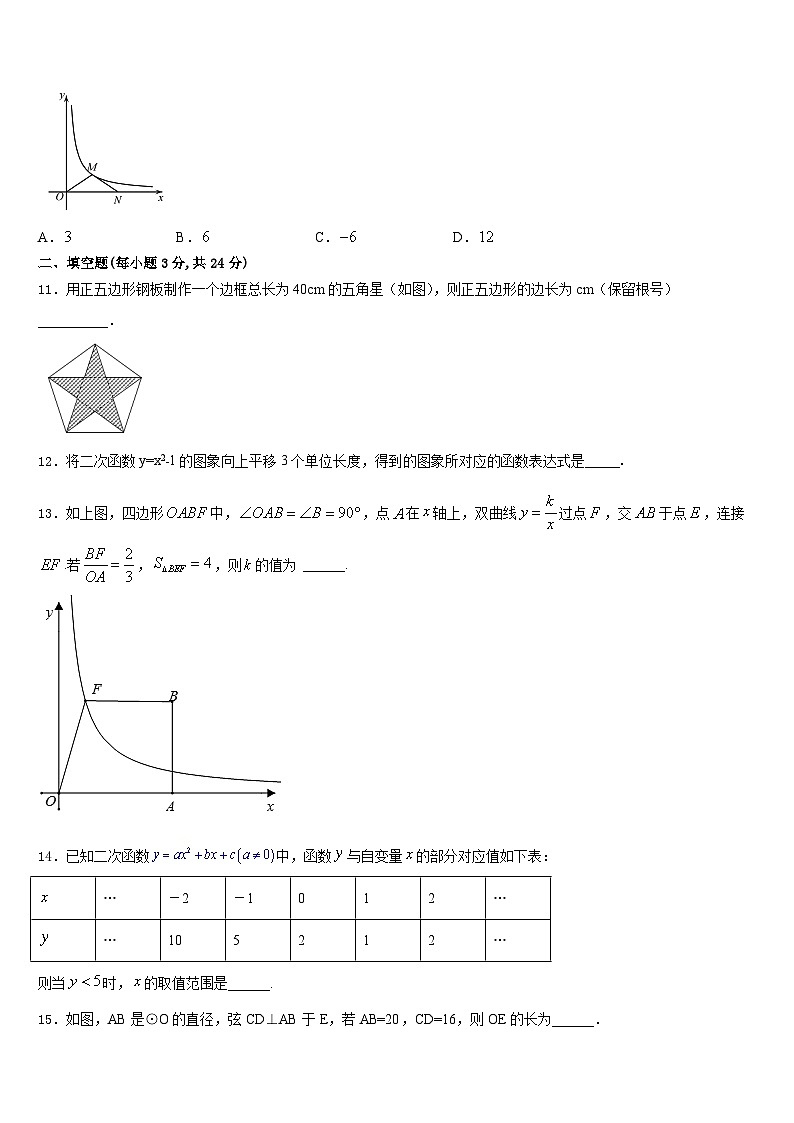
11．用正五边形钢板制作一个边框总长为40cm的五角星（如图），则正五边形的边长为cm（保留根号）__________．
12．将二次函数y=x2﹣1的图象向上平移3个单位长度，得到的图象所对应的函数表达式是_____．
13．如上图，四边形中，，点在轴上，双曲线过点，交于点，连接.若，，则的值为 ______.
14．已知二次函数中，函数与自变量的部分对应值如下表：
则当时，的取值范围是______.
15．如图，AB是⊙O的直径，弦CD⊥AB于E，若AB=20，CD=16，则OE的长为______．
16．半径为4 cm，圆心角为60°的扇形的面积为 cm1．
17．将二次函数化成的形式为__________．
18．如图，O为Rt△ABC斜边中点，AB=10，BC=6，M、N在AC边上，若△OMN∽△BOC，点M的对应点是O，则CM=______．
三、解答题(共66分)
19．（10分）数学活动课上，张老师引导同学进行如下探究：如图1，将长为的铅笔斜靠在垂直于水平桌面的直尺的边沿上，一端固定在桌面上，图2是示意图．
活动一
如图3，将铅笔绕端点顺时针旋转，与交于点，当旋转至水平位置时，铅笔的中点与点重合．

数学思考
（1）设，点到的距离．
①用含的代数式表示：的长是_________，的长是________；
②与的函数关系式是_____________，自变量的取值范围是____________．
活动二
（2）①列表：根据（1）中所求函数关系式计算并补全表格．
②描点：根据表中数值，描出①中剩余的两个点．
③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象．
数学思考
（3）请你结合函数的图象，写出该函数的两条性质或结论．
20．（6分）如图，一艘船由A港沿北偏东65°方向航行90km至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，求A，C两港之间的距离．
21．（6分）如图，已知A(-4，2)、B(n，-4)是一次函数的图象与反比例函数的图象的两个交点.
（1）求此反比例函数和一次函数的解析式；
（2）求△AOB的面积；
22．（8分）在平面直角坐标系中的位置如图所示.
在图中画出关于轴对称的图形，并写出顶点的坐标；
将向下平移个单位长度，再向左平移个单位长度得到，画出平移后的，并写出顶点的坐标.
23．（8分）如图，已知直线y＝kx+b与反比例函数y＝（x＞0）的图象交于A（1，4）、B（4，1）两点，与x轴交于C点．
（1）求一次函数与反比例函数的解析式；
（2）根据图象直接回答：在第一象限内，当x取何值时，一次函数值大于反比例函数值？
（3）点P是y＝（x＞0）图象上的一个动点，作PQ⊥x轴于Q点，连接PC，当S△CPQ＝S△CAO时，求点P的坐标．
24．（8分）某商店购进一批成本为每件 30 元的商品，经调查发现，该商品每天的销售量 y（件）与销售单价 x（元）之间满足一次函数关系，其图象如图所示.
（1）求该商品每天的销售量 y 与销售单价 x 之间的函数关系式；
（2）若商店按单价不低于成本价，且不高于 50 元销售，则销售单价定为多少，才能使销售该商品每天获得的利润 w（元）最大？最大利润是多少？
（3）若商店要使销售该商品每天获得的利润不低于 800 元，则每天的销售量最少应为多少件？
25．（10分）如图，已知直线y1＝﹣x+3与x轴交于点B，与y轴交于点C，抛物y2＝ax2+bx+c经过点B，C并与x轴交于点A（﹣1，0）．
（1）求抛物线解析式，并求出抛物线的顶点D坐标 ；
（2）当y2＜0时、请直接写出x的取值范围 ；
（3）当y1＜y2时、请直接写出x的取值范围 ；
（4）将抛物线y2向下平移，使得顶点D落到直线BC上，求平移后的抛物线解析式 ．
26．（10分）通过实验研究，专家们发现：初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的．讲课开始时，学生的兴趣激增，中间有一段时间的兴趣保持平稳状态，随后开始分散．学生注意力指标数随时间()变化的函数图象如图所示(越大表示注意力越集中)．当时，图象是抛物线的一部分，当和时，图象是线段．
（1）当时，求注意力指标数与时间的函数关系式．
（2）一道数学综合题，需要讲解24，问老师能否安排，使学生听这道题时，注意力的指标数都不低于1．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、A
3、A
4、A
5、C
6、A
7、D
8、D
9、D
10、B
二、填空题(每小题3分,共24分)
11、
12、y=x1+1
13、6
14、
15、6
16、.
17、
18、
三、解答题(共66分)
19、 (1) ），，;(2)见解析；（3）①随着的增大而减小；②图象关于直线对称；③函数的取值范围是．
20、（90+30）km．
21、 (1)y=－；y=－x－2；(2)6
22、（1）作图见解析，；（2）作图见解析，
23、（1）y＝﹣x+1；（2）当1＜x＜4时，一次函数值大于反比例函数值；（3）
24、（1）；（2）时，w最大；（3）时，每天的销售量为20件.
25、（1）；（2）x＜﹣1或x＞3；（3）0＜x＜3；（4）y＝-x2+2x+1．
26、（1）y=+20(0≤x≤10)；（2）能，理由见解析．
选手
甲
乙
丙
丁
方差
1.5
2.6
3.5
3.68
…
－2
－1
0
1
2
…
…
10
5
2
1
2
…
6
5
4
3.5
3
2.5
2
1
0.5
0
0
0.55
1.2
1.58
1.0
2.47
3
4.29
5.08