

天津市滨海新区第四共同体2023-2024学年九年级数学第一学期期末联考模拟试题含答案
展开学校_______ 年级_______ 姓名_______
考生请注意:
1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.小明和小华玩“石头、剪子、布”的游戏.若随机出手一次,则小华获胜的概率是( )
A.B.C.D.
2.下列说法正确的是( )
A.所有等边三角形都相似B.有一个角相等的两个等腰三角形相似
C.所有直角三角形都相似D.所有矩形都相似
3.在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中成立的是( )
A.B.C.D.
4.如图,BD是菱形ABCD的对角线,CE⊥AB交于点E,交BD于点F,且点E是AB中点,则tan∠BFE的值是( )
A.B.2C.D.
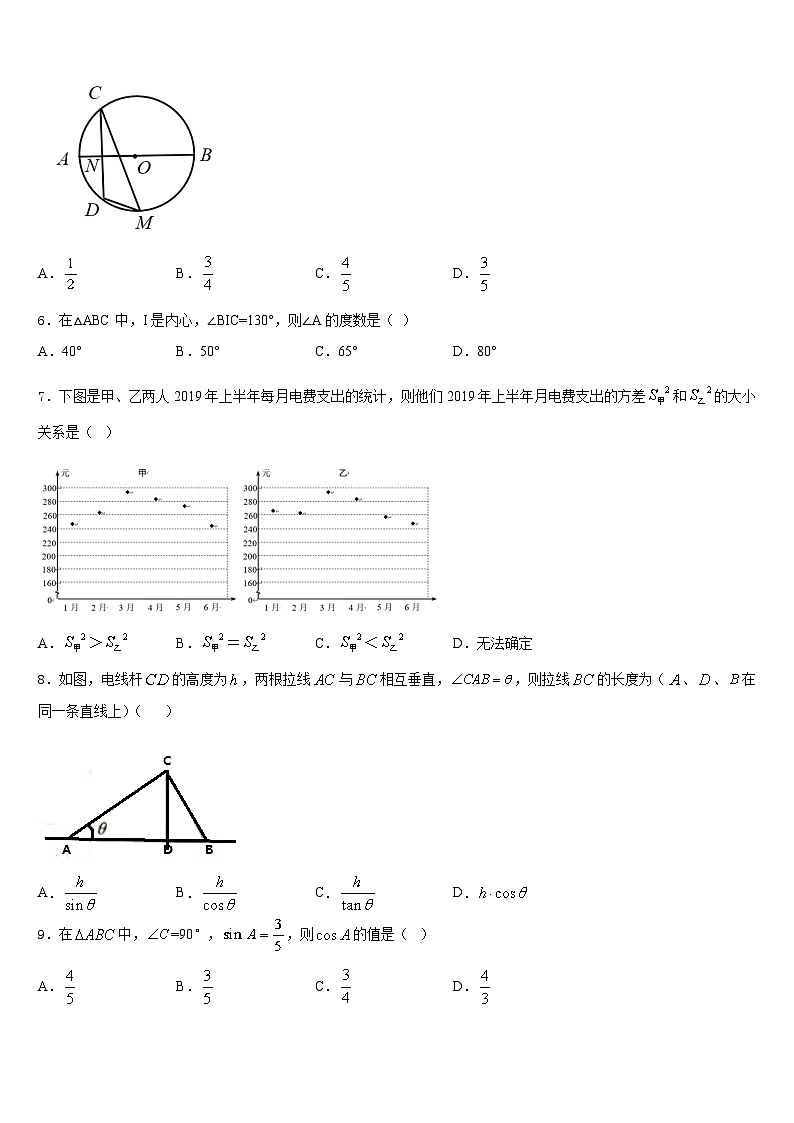
5.如图,线段是⊙的直径,弦,垂足为,点是上任意一点, ,则的值为( )
A.B.C.D.
6.在△ABC中,I是内心,∠BIC=130°,则∠A的度数是( )
A.40°B.50°C.65°D.80°
7.下图是甲、乙两人2019年上半年每月电费支出的统计,则他们2019年上半年月电费支出的方差和的大小关系是( )
A.>B.=C.<D.无法确定
8.如图,电线杆的高度为,两根拉线与相互垂直,,则拉线的长度为(、、在同一条直线上)( )
A.B.C.D.
9.在中,=90〫,,则的值是( )
A.B.C.D.
10.已知是单位向量,且,那么下列说法错误的是( )
A. ∥B.||=2C.||=﹣2||D. =﹣
二、填空题(每小题3分,共24分)
11.在直角坐标平面内,抛物线在对称轴的左侧部分是______的.
12.如图,RtΔABC绕直角顶点C顺时针旋转90°,得到ΔDEC,连接AD,若∠BAC=25°,则∠ADE=_________
13.在比例尺为1:3000000的地图上,测得AB两地间的图上距离为5厘米,则AB两地间的实际距离是______千米.
14.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x﹣3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②x=0时,y2=5;③当x>3时,y1﹣y2>0;④y轴是线段BC的中垂线.正确结论是________(填写正确结论的序号).
15.小杰在楼下点A处看到楼上点B处的小明的仰角是42度,那么点B处的小明看点A处的小杰的俯角等于_____度.
16.如图是二次函数y=ax2﹣bx+c的图象,由图象可知,不等式ax2﹣bx+c<0的解集是_______.
17.己知圆锥的母线长为,底面半径为,则它的侧面积为__________(结果保留).
18.如果关于x的方程x2-5x + a = 0有两个相等的实数根,那么a=_____.
三、解答题(共66分)
19.(10分)如图,某科技物展览大厅有A、B两个入口,C、D、E三个出口.小昀任选一个入口进入展览大厅, 参观结束后任选一个出口离开.
(1)若小昀已进入展览大厅,求他选择从出口C离开的概率.
(2)求小昀选择从入口A进入,从出口E离开的概率.(请用列表或画树状图求解)
20.(6分)计划开设以下课外活动项目:A 一版画、B 一机器人、C 一航模、D 一园艺种植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查(每位学生 必须选且只能选一个项目),并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;扇形统计图中,选“D一园艺种植”的学生人数所占圆心角的度数是 °;
(2)请你将条形统计图补充完整;
(3)若该校学生总数为 1500 人,试估计该校学生中最喜欢“机器人”和最喜欢“航模”项目的总 人数
21.(6分)京剧脸谱是京剧艺术独特的表现形式.京剧表演中,经常用脸谱象征人物的性格,品质,甚至角色和命运.如红脸代表忠心耿直,黑脸代表强悍勇猛.现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.
请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率.(图案为“红脸”的两张卡片分别记为A1、A2,图案为“黑脸”的卡片记为B)
22.(8分)如图,与是位似图形,点O是位似中心, , ,求DE的长.
23.(8分)如图,一次函数y=kx+1(k≠0)与反比例函数y= (m≠0)的图象有公共点A(1,2),直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别相交于点B,C,连接AC.
(1)求k和m的值;
(2)求点B的坐标;
(3)求△ABC的面积.
24.(8分)如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
25.(10分)小红想利用阳光下的影长测量学校旗杆AB的高度.如图,她在地面上竖直立一根2米长的标杆CD,某一时刻测得其影长DE=1.2米,此时旗杆AB在阳光下的投影BF=4.8米,AB⊥BD,CD⊥BD.请你根据相关信息,求旗杆AB的高.
26.(10分)如图,已知抛物线经过原点O,顶点为A(1,1),且与直线交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求△ABC的面积;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、A
2、A
3、B
4、D
5、D
6、D
7、A
8、B
9、A
10、C
二、填空题(每小题3分,共24分)
11、下降
12、20°
13、150
14、①③④
15、1
16、x<-1或x>1
17、
18、
三、解答题(共66分)
19、 (1); (2)
20、(1)200;72(2)60(人),图见解析(3)1050人.
21、
22、1
23、(1)k的值为1,m的值为2;(2)点B的坐标为(3,4);(3)△ABC的面积是.
24、(1)见解析;(2)3
25、旗杆AB的高为8m.
26、(1)y=﹣(x﹣1)2+1,C(﹣1,﹣3);(2)3;(3)存在满足条件的N点,其坐标为(,0)或(,0)或(﹣1,0)或(5,0)
天津市滨海新区2023-2024学年数学九年级第一学期期末调研试题含答案: 这是一份天津市滨海新区2023-2024学年数学九年级第一学期期末调研试题含答案,共8页。
2023-2024学年天津市滨海新区第四共同体数学八上期末学业水平测试试题含答案: 这是一份2023-2024学年天津市滨海新区第四共同体数学八上期末学业水平测试试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,下列各式中为最简二次根式的是,已知A等内容,欢迎下载使用。
天津市滨海新区第四共同体2022-2023学年数学七下期末达标检测模拟试题含答案: 这是一份天津市滨海新区第四共同体2022-2023学年数学七下期末达标检测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,分式方程的解为,下列等式成立的是,下列调查方式中适合的是,若解方程会产生增根,则m等于等内容,欢迎下载使用。












