2023-2024学年贵州省思南县联考九年级数学第一学期期末预测试题含答案

这是一份2023-2024学年贵州省思南县联考九年级数学第一学期期末预测试题含答案，共8页。试卷主要包含了中，，是边上的高，若，则等于等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生须知：
1．全卷分选择题和非选择题两部分，全部在答题纸上作答。选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。
一、选择题(每小题3分,共30分)
1．若，则的值为（ ）
A．1B．C．D．
2．如图，将△ABC绕点A顺时针旋转 60°得到△AED，若线段AB=3，则BE=（ ）
A．2B．3C．4D．5
3．如图所示的是几个完全相同的小正方体搭建成的几何体的俯视图，其中小正方形内的数字为对应位置上的小正方体的个数，则该几何体的左视图为( )
A．B．C．D．
4．袋中装有除颜色外其他完全相同的4个小球，其中3个红色，一个白色，从袋中任意地摸出两个球，这两个球颜色相同的概率是( )
A．B．C．D．
5．若关于的一元二次方程有两个相等的根，则的值为（ ）
A．B．C．或D．或
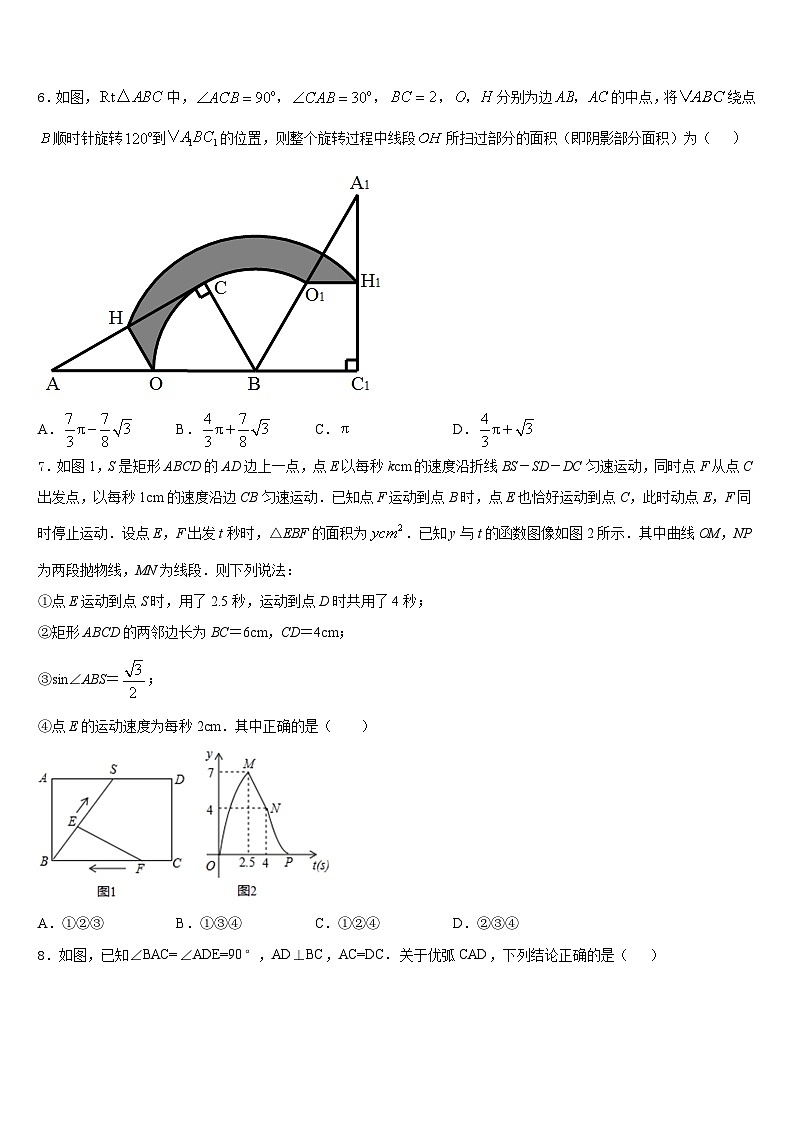
6．如图，中，，，，分别为边的中点，将绕点顺时针旋转到的位置，则整个旋转过程中线段所扫过部分的面积（即阴影部分面积）为（ ）
A．B．C．D．
7．如图1，S是矩形ABCD的AD边上一点，点E以每秒kcm的速度沿折线BS－SD－DC匀速运动，同时点F从点C出发点，以每秒1cm的速度沿边CB匀速运动．已知点F运动到点B时，点E也恰好运动到点C，此时动点E，F同时停止运动．设点E，F出发t秒时，△EBF的面积为．已知y与t的函数图像如图2所示．其中曲线OM，NP为两段抛物线，MN为线段．则下列说法：
①点E运动到点S时，用了2.5秒，运动到点D时共用了4秒；
②矩形ABCD的两邻边长为BC＝6cm，CD＝4cm；
③sin∠ABS＝；
④点E的运动速度为每秒2cm．其中正确的是（ ）
A．①②③B．①③④C．①②④D．②③④
8．如图，已知∠BAC=∠ADE=90°，AD⊥BC，AC=DC．关于优弧CAD，下列结论正确的是（ ）
A．经过点B和点EB．经过点B，不一定经过点E
C．经过点E，不一定经过点BD．不一定经过点B和点E
9．如图，正方形ABCD的边长为3，点E、F分别在边BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G处，已知BE＝1，则EF的长为（ ）
A．B．C．D．3
10．中，，是边上的高，若，则等于（ ）
A．B．或C．D．或
二、填空题(每小题3分,共24分)
11．如图，在△ABC中，AC：BC：AB＝3：4：5，⊙O沿着△ABC的内部边缘滚动一圈，若⊙O的半径为1，且圆心O运动的路径长为18，则△ABC的周长为_____．
12．分解因式:__________．
13．把多项式分解因式的结果是 ．
14．在一个不透明的盒子中装有6个白球，x个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，摸到白球的概率为，则x=_______．
15．二次函数中的自变量与函数值的部分对应值如下表：
则的解为________．
16．如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y＝（k≠0）在第一象限的图象经过顶点A(m，2)和CD边上的点E(n，)，则点D的坐标是_____．
17．如图，在平面直角坐标系中，已知函数和，点为轴正半轴上一点，为轴上一点，过作轴的垂线分别交，的图象于，两点，连接，，则的面积为_________ ．
18．已知二次函数的图象如图所示，下列结论：①；②；③；④，其中正确的是_________．（把所有正确结论的序号都填在横线上）
三、解答题(共66分)
19．（10分）某汽车零部件生产企业的利润逐年提高，据统计，2015年利润为2亿元，2017年利润为2.88亿元，求该企业从2015年到2017年利润的年平均增长率．
20．（6分）我区某校组织了一次“诗词大会”，张老师为了选拔本班学生参加，对本班全体学生诗词的掌握情况进行了调查，并将调查结果分为了三类：A：好，B：中，C：差．请根据图中信息，解答下列问题：
（1）全班学生共有 人；
（2）扇形统计图中，B类占的百分比为 %，C类占的百分比为 %；
（3）将上面的条形统计图补充完整；
（4）小明被选中参加了比赛．比赛中有一道必答题是：从下表所示的九宫格中选取七个字组成一句诗，其答案为“便引诗情到碧霄”．小明回答该问题时，对第四个字是选“情”还是选“青”，第七个字是选“霄”还是选“宵”，都难以抉择，若分别随机选择，请用列表或画树状图的方法求小明回答正确的概率．
21．（6分）如图，一块直角三角板的直角顶点P放在正方形ABCD的BC边上，并且使条直角边经过点D，另一条直角边与AB交于点Q．请写出一对相似三角形，并加以证明．(图中不添加字母和线段)
22．（8分）如图，在△ABC中，∠C＝90°，P为AB上一点，且点P不与点A重合，过点P作PE⊥AB交AC边于E点，点E不与点C重合，若AB＝10，AC＝8，设AP的长为x，四边形PECB的周长为y，
（1）试证明：△AEP∽△ABC；
（2）求y与x之间的函数关系式．
23．（8分）如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M．
（1）求证：△AHF为等腰直角三角形．
（2）若AB＝3，EC＝5，求EM的长．
24．（8分）（1）计算：4sin260°+tan45°-8cs230°
（2）在Rt△ABC中，∠C=90°．若∠A=30°，b=5，求a、c．
25．（10分）如图1，▱ABCD中，∠ABC、∠ADC的平分线分别交AD、BC于点E、F．
（1）求证：四边形EBFD是平行四边形；
（2）如图2，小明在完成（1）的证明后继续进行了探索．连接AF、CE，分别交BE、FD于点G、H，得到四边形EGFH．此时，他猜想四边形EGFH是平行四边形，请在框图（图3）中补全他的证明思路，再在答题纸上写出规范的证明过程．
26．（10分）如图，在Rt△ABC中，∠BAC＝90°，BD是角平分线，以点D为圆心，DA为半径的⊙D与AC相交于点E.
(1)求证：BC是⊙D的切线；
(2)若AB＝5，BC＝13，求CE的长．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、B
3、A
4、A
5、B
6、C
7、C
8、B
9、B
10、B
二、填空题(每小题3分,共24分)
11、4
12、
13、m（4m+n）（4m﹣n）．
14、1
15、或
16、 (3，2)
17、1
18、①②③
三、解答题(共66分)
19、该企业从2015年到2017年利润的年平均增长率为20%
20、（1）40；（2）60，15；（3）补全条形统计图见解析；（4）小明回答正确的概率是．
21、△BPQ∽△CDP，证明见解析.
22、（1）见解析；（2）y=．（0＜x＜6.4）
23、（1）见解析；（2）EM＝
24、（1）2 ；（2）a=5，c=1
25、（1）证明见解析；（2）证明见解析
26、 (1)证明详见解析；(2)．
…
…
…
…
情
到
碧
霄
诗
青
引
宵
便