2023-2024学年云南省昆明市九年级数学第一学期期末学业水平测试模拟试题含答案

这是一份2023-2024学年云南省昆明市九年级数学第一学期期末学业水平测试模拟试题含答案，共7页。试卷主要包含了考生必须保证答题卡的整洁，一元二次方程有实数解的条件等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1．如图，AB，BC是⊙O的两条弦，AO⊥BC，垂足为D，若⊙O的半径为5，BC＝8，则AB的长为（ ）
A．8B．10C．D．
2．如图，在等腰Rt△ABC中，∠BAC＝90°，BC＝2，点P是△ABC内部的一个动点，且满足∠PBC＝∠PCA，则线段AP长的最小值为（ ）
A．0.5B．﹣1C．2﹣D．
3．如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是
A．AC=ABB．∠C=∠BODC．∠C=∠BD．∠A=∠B0D
4．如图,在同一直角坐标系中,正比例函数y=kx+3与反比例函数的图象位置可能是（ ）
A．B．C．D．
5．如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点0）20米的A处，则小明的影长为（ ）米．
A．4B．5C．6D．7
6．现有两组相同的牌，每组三张且大小一样，三张牌的牌面数字分别是1、2、3，从每组牌中各摸出一张牌．两张牌的牌面数字之和等于4的概率是（ ）
A．B．C．D．
7．已知的半径为，点的坐标为，点的坐标为，则点与的位置关系是（ ）
A．点在外B．点在上C．点在内D．不能确定
8．口袋中有2个红球和1个黑球，每次摸到后放回，两次都摸到红球的概率为（ ）
A．B．C．D．
9．如图所示，△的顶点是正方形网格的格点，则的值是（ ）
A．B．C．D．
10．一元二次方程有实数解的条件( )
A．B．C．D．
二、填空题(每小题3分,共24分)
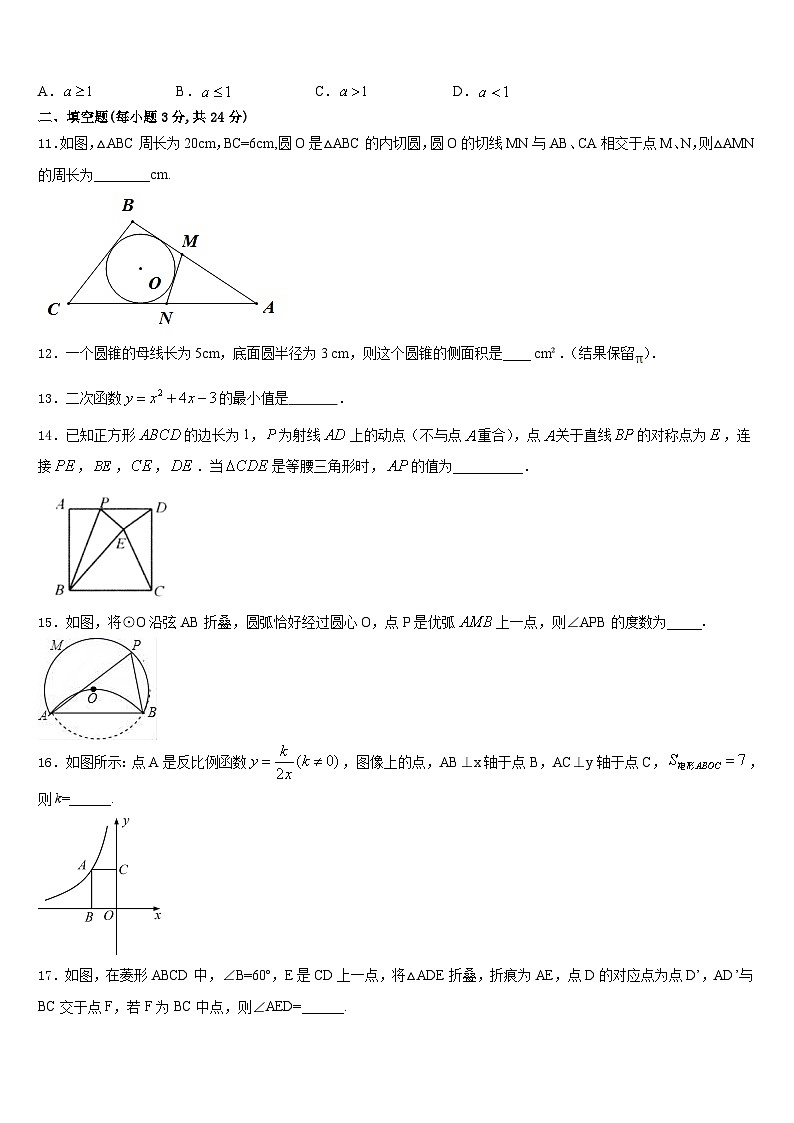
11．如图，△ABC周长为20cm，BC=6cm,圆O是△ABC的内切圆，圆O的切线MN与AB、CA相交于点M、N，则△AMN的周长为________cm.
12．一个圆锥的母线长为5cm，底面圆半径为3 cm，则这个圆锥的侧面积是____ cm²．（结果保留）．
13．二次函数的最小值是 ．
14．已知正方形的边长为1，为射线上的动点（不与点重合），点关于直线的对称点为，连接，，，．当是等腰三角形时，的值为__________．
15．如图，将⊙O沿弦AB折叠，圆弧恰好经过圆心O，点P是优弧上一点，则∠APB的度数为_____．
16．如图所示：点A是反比例函数，图像上的点，AB⊥x轴于点B，AC⊥y轴于点C，，则k=______.
17．如图，在菱形ABCD中，∠B=60º，E是CD上一点，将△ADE折叠，折痕为AE，点D的对应点为点D’，AD’与BC交于点F，若F为BC中点，则∠AED=______.
18．如图，在Rt△ABC中，∠C＝90°，AC＝6，AD∥BC，DE与AB交于点F，已知AD＝4，DF＝2EF，sin∠DAB＝，则线段DE＝_____．
三、解答题(共66分)
19．（10分）如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC＝∠A，连接OE延长与圆相交于点F，与BC相交于点C．
（1）求证：BC是⊙O的切线；
（2）若⊙O的半径为6，BC＝8，求弦BD的长．
20．（6分）某超市销售一种饮料， 每瓶进价为元，当每瓶售价元时，日均销售量瓶.经市场调查表明，每瓶售价每增加元，日均销售量减少瓶.
（1）当每瓶售价为元时，日均销售量为 瓶；
（2）当每瓶售价为多少元时，所得日均总利润为元；
（3）当每瓶售价为多少元时，所得日均总利润最大？最大日均总利润为多少元？
21．（6分）如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E．求证：四边形AEOD是正方形．
22．（8分）如图，一次函数的图象与反比例函数的图象交于，两点．
（1）求一次函数和反比例函数的表达式；
（2）直接写出的面积 ．
23．（8分）已知为实数，关于的方程有两个实数根．
（1）求实数的取值范围．
（2）若，试求的值．
24．（8分）如图，已知是的直径，点是延长线上一点过点作的切线，切点为.过点作于点，延长交于点.连结，，，.若，.
（1）求的长。
（2）求证：是的切线.
（3）试判断四边形的形状，并求出四边形的面积.
25．（10分）已知x2+xy+y＝12，y2+xy+x＝18，求代数式3x2+3y2﹣2xy+x+y的值．
26．（10分）已知等边△ABC的边长为2，
（1）如图1，在边BC上有一个动点P，在边AC上有一个动点D，满足∠APD＝60°，求证：△ABP～△PCD
（2）如图2，若点P在射线BC上运动，点D在直线AC上，满足∠APD＝120°，当PC＝1时，求AD的长
（3）在（2）的条件下，将点D绕点C逆时针旋转120°到点D'，如图3，求△D′AP的面积．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、B
4、A
5、B
6、B
7、B
8、D
9、B
10、B
二、填空题(每小题3分,共24分)
11、8
12、15π
13、﹣1．
14、或或
15、60°
16、
17、75º
18、2
三、解答题(共66分)
19、（1）详见解析；（2）BD=9.6.
20、（1）；（2）元或元；（3）元时利润最大，最大利润元
21、证明见解析．
22、（1）y=﹣x+5，y=；（2）
23、（1）.（2）-3.
24、（1）BD=2；(2)见解析；（3）四边形ABCD是菱形，理由见解析. 菱形ABCD得面积为6.
25、或
26、（1）见解析；（2）；（3）