七年级数学下学期期末模拟测试卷模拟卷04（浙江杭州卷）（原卷版+解析版）

这是一份七年级数学下学期期末模拟测试卷模拟卷04（浙江杭州卷）（原卷版+解析版），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．北京2022冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作，墩墩意喻敦厚、敦实、可爱，契合熊猫的整体形象，象征着冬奥会运动员强壮有力的身体、坚韧不拔的意志和鼓舞人心的奥林匹克精神!下面选项中的四张图片，哪张可以由图平移得到（ ）
A．B．
C．D．
2．下面调查中，最适合采用全面调查的是（ ）
A．对全国中学生视力状况的调查
B．了解重庆市八年级学生身高情况
C．调查人们垃圾分类的意识
D．对“天舟三号”货运飞船零部件的调查
3．下列运算中，结果正确的是（ ）
A．a2•（a3）2＝a7B．（3x﹣2）（2x+3）＝6x2﹣6
C．（﹣3pq）2＝9p2q2D．（a﹣2）2＝a2﹣4
4．若x2﹣2（m﹣3）x+16是关于x的完全平方式，则m是（ ）
A．7或﹣1B．﹣1C．7D．5或1
5．化简的结果是（ ）
A．mB．﹣mC．m+1D．m﹣1
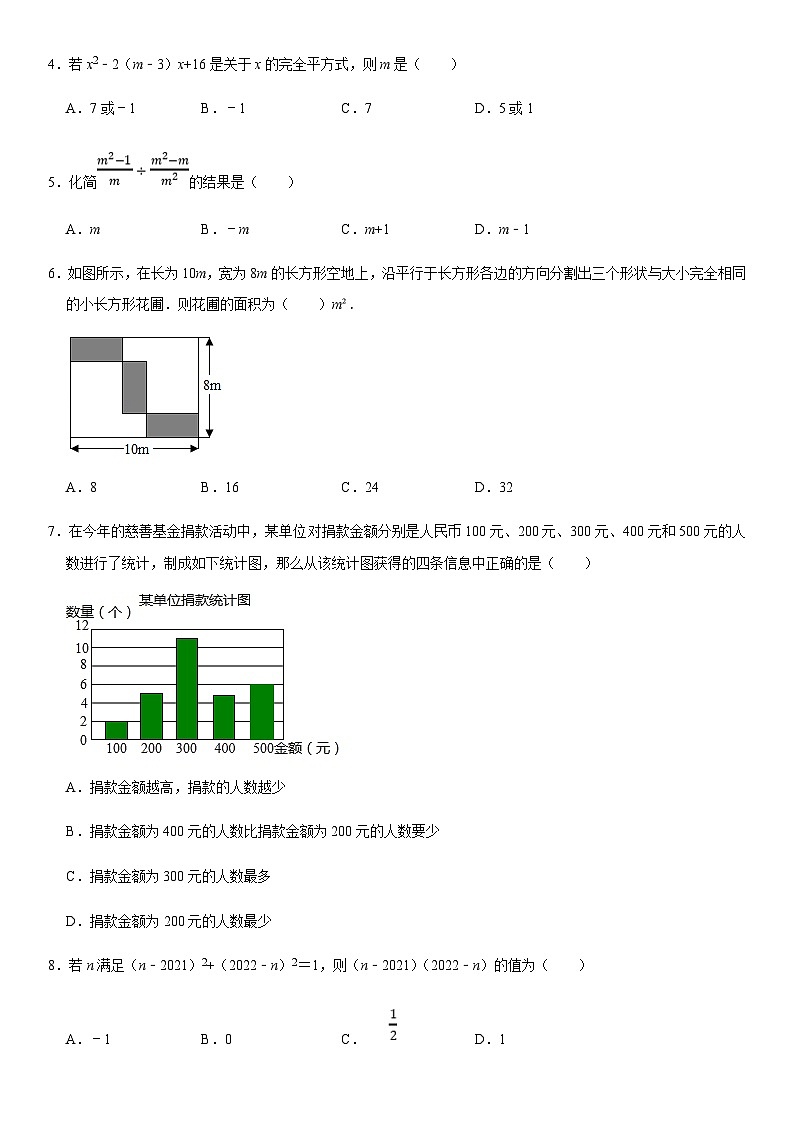
6．如图所示，在长为10m，宽为8m的长方形空地上，沿平行于长方形各边的方向分割出三个形状与大小完全相同的小长方形花圃．则花圃的面积为（ ）m²．
A．8B．16C．24D．32
7．在今年的慈善基金捐款活动中，某单位对捐款金额分别是人民币100元、200元、300元、400元和500元的人数进行了统计，制成如下统计图，那么从该统计图获得的四条信息中正确的是（ ）
A．捐款金额越高，捐款的人数越少
B．捐款金额为400元的人数比捐款金额为200元的人数要少
C．捐款金额为300元的人数最多
D．捐款金额为200元的人数最少
8．若n满足（n﹣2021）2+（2022﹣n）2＝1，则（n﹣2021）（2022﹣n）的值为（ ）
A．﹣1B．0C．D．1
9．学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的（如图（1）～（4）），从图中可知，小敏画平行线的依据有（ ）
①两直线平行，同位角相等；
②两直线平行，内错角相等；
③同位角相等，两直线平行；
④内错角相等，两直线平行．
A．①②B．②③C．③④D．①④
10．方程组的解为，则被遮盖的两个数分别为（ ）
A．9，﹣1B．9，1C．7，﹣1D．5，1
二、填空题（本大题共6小题，每小题4分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
11．若3a＝6，3b＝2，则3a+b＝ ．
12．某校开展了“科技托起强国梦”征文活动，该校对初二年级六个班上交征文的篇数进行了统计，绘制了如图所示的折线统计图，则1班上交征文篇数的频率是 ．
13．如图，已知AB∥CD，AD∥BE，∠B＝40°，∠E＝48°，则∠CDF＝ 度．
14．在长方形ABCD中放入六个完全相同的小长方形，所标尺寸如图所示，则小长方形的宽CE为 cm．
15．若m是整数，关于x、y的二元一次方程组的解是整数，则满足条件的所有m的值的和为 ．
16．如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝33°，则∠E＝ ．
三、解答题（本大题共7小题，共66分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．（6分）计算：
（1）（x+2y）（x﹣3y）+xy；
（2）12a3b2c÷（﹣2ab）2．
18．（6分）（1）解二元一次方程组；
（2）解分式方程5．
19．（8分）已知：如图，EF∥CD，∠1+∠2＝180°．
（1）判断GD与CA的位置关系，并说明理由．
（2）若DG平分∠CDB，若∠ACD＝40°，求∠A的度数．
20．（10分）为提高学生身体素质，某校决定开展足球、篮球、排球、乒乓球等四项课外体育活动，要求全员参与，并且每名学生只能选择其中一项．为了解选择各种体育活动项目的学生人数，该校随机抽取了部分学生进行调查，并绘制出如下两幅不完整的统计图，请根据统计图回答下列问题：
（1）直接写出这次抽样调查的学生人数．
（2）补全条形统计图，在扇形统计图中“篮球”所对的扇形圆心角为 度．
（3）若该学校总人数是1500人，请估计选择篮球项目的学生约有多少人？
21．（10分）阅读感悟：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：
已知实数x、y满足3x﹣y＝5①，2x+3y＝7②，求x﹣4y和7x+5y的值．
本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①﹣②可得x﹣4y＝﹣2，由①+②×2可得7x+5y＝19．这样的解题思想就是通常所说的“整体思想”．
解决问题：
（1）已知二元一次方程组则x﹣y＝ ，x+y＝ ；
（2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？
（3）对于实数x、y，定义新运算：x*y＝ax+by+c，其中a、b、c是常数，等式右边是通常的加法和乘法运算．已知3*5＝15，4*7＝28，那么1*1＝ ．
22．（12分）2021年10月17日是我国第8个扶贫日，也是第29个国际消除贫困日．为组织开展好扶贫日系列活动，加快脱贫攻坚步伐．我市决定将一批生姜送往外地销售．现有甲、乙两种货车，已知甲种货车比乙种货车每辆车多装20箱生姜，且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等．
（1）求甲、乙两种货车每辆车可装多少箱生姜？
（2）如果这批生姜有1535箱，用甲、乙两种汽车共16辆来装运，甲种车辆刚好装满，乙种车辆最后一辆只装了55箱，其它装满，求甲、乙两种货车各有多少辆？
23．（14分）完全平方公式（a±b）2＝a2±2ab+b2进行适当的变形后，可以解决很多的数学问题．
如：若x满足（9﹣x）（x﹣4）＝4，求（9﹣x）2+（x﹣4）2的值．解题思路；由（a+b）2＝a2+2ab+b2得a2+b2＝（a+b）2﹣2ab，可设9﹣x＝a，x﹣4＝b，则（9﹣x）（x﹣4）＝ab＝4，a+b＝（9﹣x）+（x﹣4）＝5，∴（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝52﹣2×4＝17；
（1）请仿照上面的方法求解下面问题：
①若x满足（5﹣x）（x﹣2）＝2，求（5﹣x）2+（x﹣2）2的值；
②若x满足（9+x）（2+x）＝4，求（9+x）2+（2+x）2的值；
（2）应用上面的解题思路解决问题：如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝6，两正方形的面积和S1+S2＝18，求图中阴影部分的面积．
七年级数学下学期期末模拟测试卷04（浙江杭州卷）
一、选择题（本大题共10小题，每小题3分，共30分。在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
1．北京2022冬奥会吉祥物“冰墩墩”以熊猫为原型进行设计创作，墩墩意喻敦厚、敦实、可爱，契合熊猫的整体形象，象征着冬奥会运动员强壮有力的身体、坚韧不拔的意志和鼓舞人心的奥林匹克精神!下面选项中的四张图片，哪张可以由图平移得到（ ）
A．B．
C．D．
解：由平移的性质可知，可以由题图平移得到的只有选项D．
答案：D．
2．下面调查中，最适合采用全面调查的是（ ）
A．对全国中学生视力状况的调查
B．了解重庆市八年级学生身高情况
C．调查人们垃圾分类的意识
D．对“天舟三号”货运飞船零部件的调查
解：A．对全国中学生视力状况的调查，适合抽样调查，故本选项不合题意；
B．了解重庆市八年级学生身高情况，适合抽样调查，故本选项不合题意；
C．调查人们垃圾分类的意识，适合抽样调查，故本选项不合题意；
D．对“天舟三号”货运飞船零部件的调查，适合普查，故本选项符合题意．
答案：D．
3．下列运算中，结果正确的是（ ）
A．a2•（a3）2＝a7B．（3x﹣2）（2x+3）＝6x2﹣6
C．（﹣3pq）2＝9p2q2D．（a﹣2）2＝a2﹣4
解：A．a2•（a3）2
＝a2•a6
＝a8，故本选项不符合题意；
B．（3x﹣2）（2x+3）
＝6x2+9x﹣4x﹣6
＝6x2+5x﹣6，故本选项不符合题意；
C．（﹣3pq）2＝9p2q2，故本选项符合题意；
D．（a﹣2）2＝a2﹣4a+4，故本选项不符合题意；
答案：C．
4．若x2﹣2（m﹣3）x+16是关于x的完全平方式，则m是（ ）
A．7或﹣1B．﹣1C．7D．5或1
解：∵x2﹣2（m﹣3）x+16是关于x的完全平方式，
∴m﹣3＝±4，
解得：m＝7或﹣1，
答案：A．
5．化简的结果是（ ）
A．mB．﹣mC．m+1D．m﹣1
解：原式•
＝m+1，
答案：C．
6．如图所示，在长为10m，宽为8m的长方形空地上，沿平行于长方形各边的方向分割出三个形状与大小完全相同的小长方形花圃．则花圃的面积为（ ）m²．
A．8B．16C．24D．32
解：设小长方形花圃的长为xm，宽为ym，
依题意有：，
解得：，
则一个小长方形花圃的面积为：4×2＝8（m2）．
∴花圃的面积＝3×8＝24（m2），
答案：C．
7．在今年的慈善基金捐款活动中，某单位对捐款金额分别是人民币100元、200元、300元、400元和500元的人数进行了统计，制成如下统计图，那么从该统计图获得的四条信息中正确的是（ ）
A．捐款金额越高，捐款的人数越少
B．捐款金额为400元的人数比捐款金额为200元的人数要少
C．捐款金额为300元的人数最多
D．捐款金额为200元的人数最少
解：由图知，捐款金额分别是人民币100元、200元、300元、400元和500元的人数分别是2，5，11，5，6．
∴选项A、B、D是错误的，正确的是C，捐款金额为300元的人数最多是11人．
答案：C．
8．若n满足（n﹣2021）2+（2022﹣n）2＝1，则（n﹣2021）（2022﹣n）的值为（ ）
A．﹣1B．0C．D．1
解：设n﹣2021＝x，2022﹣n＝y，
∴x+y
＝n﹣2021+2022﹣n
＝1，
∵（n﹣2021）2+（2022﹣n）2＝1，
∴x2+y2＝1，
∵x+y＝1，
∴（x+y）2＝1，
∴x2+2xy+y2＝1，
∴xy＝0，
∴（n﹣2021）（2022﹣n）＝0，
答案：B．
9．学习了平行线后，小敏想出了过已知直线外一点画这条直线的平行线的新方法，她是通过折一张半透明的纸得到的（如图（1）～（4）），从图中可知，小敏画平行线的依据有（ ）
①两直线平行，同位角相等；
②两直线平行，内错角相等；
③同位角相等，两直线平行；
④内错角相等，两直线平行．
A．①②B．②③C．③④D．①④
解：由作图过程可知，∠1＝∠2，为内错角相等；∠1＝∠4，为同位角相等；
可知小敏画平行线的依据有：③同位角相等，两直线平行；④内错角相等，两直线平行．
答案：C．
10．方程组的解为，则被遮盖的两个数分别为（ ）
A．9，﹣1B．9，1C．7，﹣1D．5，1
解：解方程组得，
第二个被遮盖的数为﹣1，
所以第一个被遮盖的数为2×4﹣1＝7．
答案：C．
二、填空题（本大题共6小题，每小题4分，共24分。不需写出解答过程，请将答案直接填写在答题卡相应位置上）
11．若3a＝6，3b＝2，则3a+b＝ 12 ．
解：∵3a＝6，3b＝2，
∴原式＝3a•3b
＝6×2
＝12．
答案：12．
12．某校开展了“科技托起强国梦”征文活动，该校对初二年级六个班上交征文的篇数进行了统计，绘制了如图所示的折线统计图，则1班上交征文篇数的频率是 ．
解：根据折线统计图可知：初二年级六个班上交征文篇数的总和为：
8+2+3+5+6+3＝27．
所以1班上交征文篇数的频率是．
答案：．
13．如图，已知AB∥CD，AD∥BE，∠B＝40°，∠E＝48°，则∠CDF＝ 88 度．
解：∵AB∥CD，
∴∠DCE＝∠B＝40°，
又∵∠CDF是△CDE的外角，
∴∠CDF＝∠E+∠DCE＝48°+40°＝88°，
答案：88．
14．在长方形ABCD中放入六个完全相同的小长方形，所标尺寸如图所示，则小长方形的宽CE为 2 cm．
解：设小长方形的长为xcm，宽为ycm，
则AD＝x+3y，AB＝x+y＝5+2y，
即x﹣y＝5，
根据题意，得：，
解得：，
即CE＝2cm，
答案：2．
15．若m是整数，关于x、y的二元一次方程组的解是整数，则满足条件的所有m的值的和为 ﹣12 ．
解：，
①+②得，（m+3）x＝10，
解得x（m≠﹣3），
当x＝10时，m+3＝1，解得m＝﹣2；
当x＝5时，m+3＝2，解得m＝﹣1；
当x＝2时，m+3＝5，解得m＝2；
当x＝1时，m+3＝10，解得m＝7；
当x＝﹣1时，m+3＝﹣10，解得m＝﹣13，
当x＝﹣2时，m+3＝﹣5，解得m＝﹣8，
当x＝﹣5时，m+3＝﹣2，解得m＝﹣5，
当x＝﹣10时，m+3＝﹣1，解得m＝﹣4，
当m＝﹣13，﹣5，﹣1，7时，y不是整数，
∴符合条件的所有m的值的和为
∴﹣8﹣4﹣2+2＝﹣12，
答案：﹣12．
16．如图，AB∥CD，∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，∠E﹣∠F＝33°，则∠E＝ 82° ．
解：如图，过F作FH∥AB，
∵AB∥CD，
∴FH∥AB∥CD，
∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F，
∴可设∠ABF＝∠EBF＝α＝∠BFH，∠DCG＝∠ECG＝β＝∠CFH，
∴∠ECF＝180°﹣β，∠BFC＝∠BFH﹣∠CFH＝α﹣β，
∴四边形BFCE中，∠E+∠BFC＝360°﹣α﹣（180°﹣β）＝180°﹣（α﹣β）＝180°﹣∠BFC，
即∠E+2∠BFC＝180°，①
又∵∠E﹣∠BFC＝33°，
∴∠BFC＝∠E﹣33°，②
∴由①②可得，∠E+2（∠E﹣33°）＝180°，
解得∠E＝82°，
答案：82°．
三、解答题（本大题共7小题，共66分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
17．计算：
（1）（x+2y）（x﹣3y）+xy；
（2）12a3b2c÷（﹣2ab）2．
解：（1）原式＝x2﹣3xy+2xy﹣6y2+xy
＝x2﹣6y2；
（2）原式＝12a3b2c÷4a2b2
＝3ac．
18．（1）解二元一次方程组；
（2）解分式方程5．
解：（1），
把①代入②得：3（1﹣y）+y＝1，
解得：y＝1，
把y＝1代入①，得：x＝1﹣1＝0，
所以原方程组的解为；
（2）5，
方程两边都乘以x（x+3），得x+3+5x2＝5x（x+3），
解得：，
检验，当时，x（x+3）≠0，
所以x是原方程的解，
即原方程的解是x．
19．已知：如图，EF∥CD，∠1+∠2＝180°．
（1）判断GD与CA的位置关系，并说明理由．
（2）若DG平分∠CDB，若∠ACD＝40°，求∠A的度数．
解：（1）GD∥CA．
理由：∵EF∥CD，
∴∠1+∠ACD＝180°，
又∵∠1+∠2＝180°，
∴∠ACD＝∠2，
∴GD∥CA；
（2）∵GD∥CA，
∴∠2＝∠ACD＝40°，
∵DG平分∠CDB，
∴∠BDG＝∠2＝40°，
∵GD∥CA，
∴∠A＝∠BDG＝40°．
20．为提高学生身体素质，某校决定开展足球、篮球、排球、乒乓球等四项课外体育活动，要求全员参与，并且每名学生只能选择其中一项．为了解选择各种体育活动项目的学生人数，该校随机抽取了部分学生进行调查，并绘制出如下两幅不完整的统计图，请根据统计图回答下列问题：
（1）直接写出这次抽样调查的学生人数．
（2）补全条形统计图，在扇形统计图中“篮球”所对的扇形圆心角为 144 度．
（3）若该学校总人数是1500人，请估计选择篮球项目的学生约有多少人？
解：（1）140÷35%＝400（人），
即这次抽样调查的学生一共有400人；
（2）参加篮球的学生有：400﹣140﹣20﹣80＝160（人），
补全的条形统计图如右图所示，
在扇形统计图中“篮球”所对的扇形圆心角为：360°144°，
答案：144；
（3）1500600（人），
答：估计选择篮球项目的学生约有600人．
21．阅读感悟：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：
已知实数x、y满足3x﹣y＝5①，2x+3y＝7②，求x﹣4y和7x+5y的值．
本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①﹣②可得x﹣4y＝﹣2，由①+②×2可得7x+5y＝19．这样的解题思想就是通常所说的“整体思想”．
解决问题：
（1）已知二元一次方程组则x﹣y＝ ﹣1 ，x+y＝ 5 ；
（2）某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？
（3）对于实数x、y，定义新运算：x*y＝ax+by+c，其中a、b、c是常数，等式右边是通常的加法和乘法运算．已知3*5＝15，4*7＝28，那么1*1＝ ﹣11 ．
解：（1）．
由①﹣②可得：x﹣y＝﹣1，
由（①+②）可得：x+y＝5．
答案：﹣1；5．
（2）设铅笔的单价为m元，橡皮的单价为n元，日记本的单价为p元，
依题意，得：，
由2×①﹣②可得m+n+p＝6，
∴5m+5n+5p＝5×6＝30．
答：购买5支铅笔、5块橡皮、5本日记本共需30元．
（3）依题意，得：，
由3×①﹣2×②可得：a+b+c＝﹣11，
即1*1＝﹣11．
答案：﹣11．
22．2021年10月17日是我国第8个扶贫日，也是第29个国际消除贫困日．为组织开展好扶贫日系列活动，加快脱贫攻坚步伐．我市决定将一批生姜送往外地销售．现有甲、乙两种货车，已知甲种货车比乙种货车每辆车多装20箱生姜，且甲种货车装运1000箱生姜所用车辆与乙种货车装运800箱生姜所用车辆相等．
（1）求甲、乙两种货车每辆车可装多少箱生姜？
（2）如果这批生姜有1535箱，用甲、乙两种汽车共16辆来装运，甲种车辆刚好装满，乙种车辆最后一辆只装了55箱，其它装满，求甲、乙两种货车各有多少辆？
解：（1）设每辆乙种货车可装x箱生姜，则每辆甲种货车可装（x+20）箱生姜，
依题意得：，
解得：x＝80，
经检验，x＝80是原方程的解，且符合题意，
∴x+20＝80+20＝100．
答：每辆甲种货车可装100箱生姜，每辆乙种货车可装80箱生姜．
（2）设甲种货车有m辆，则乙种货车有（16﹣m）辆，
依题意得：100m+80（16﹣m﹣1）+55＝1535，
解得：m＝14，
∴16﹣m＝16﹣14＝2．
答：甲种货车有14辆，乙种货车有2辆．
23．完全平方公式（a±b）2＝a2±2ab+b2进行适当的变形后，可以解决很多的数学问题．
如：若x满足（9﹣x）（x﹣4）＝4，求（9﹣x）2+（x﹣4）2的值．解题思路；由（a+b）2＝a2+2ab+b2得a2+b2＝（a+b）2﹣2ab，可设9﹣x＝a，x﹣4＝b，则（9﹣x）（x﹣4）＝ab＝4，a+b＝（9﹣x）+（x﹣4）＝5，∴（9﹣x）2+（x﹣4）2＝a2+b2＝（a+b）2﹣2ab＝52﹣2×4＝17；
（1）请仿照上面的方法求解下面问题：
①若x满足（5﹣x）（x﹣2）＝2，求（5﹣x）2+（x﹣2）2的值；
②若x满足（9+x）（2+x）＝4，求（9+x）2+（2+x）2的值；
（2）应用上面的解题思路解决问题：如图，点C是线段AB上的一点，以AC，BC为边向两边作正方形，设AB＝6，两正方形的面积和S1+S2＝18，求图中阴影部分的面积．
解：（1）①设5﹣x＝a，x﹣2＝b，则（5﹣x）（x﹣2）＝ab＝2，a+b＝（5﹣x）+（x﹣2）＝3，
∴（5﹣x）2+（x﹣2）2＝a2+b2＝（a+b）2﹣2ab＝32﹣2×2＝5；
②设9+x＝a，2+x＝b，则（9+x）（2+x）＝ab＝4，a﹣b＝（9+x）﹣（2+x）＝7，
∴（9+x）2+（2+x）2＝a2+b2＝（a﹣b）2+2ab＝72+2×4＝57；
（2）设AC＝a，BC＝CF＝b，
则a+b＝6，a2+b2＝18，
∵a2+b2＝（a+b）2﹣2ab，
∴18＝36﹣2ab，
∴ab＝9，
∴S阴影ab．