第12讲 向量的数量积-【预习】高一数学寒假衔接讲义练习（人教B版 必修第三册）

这是一份第12讲 向量的数量积-【预习】高一数学寒假衔接讲义练习（人教B版 必修第三册），文件包含第12讲向量的数量积教师卷-预习高一数学寒假精品衔接讲义练习人教B版必修第三册docx、第12讲向量的数量积学生卷-预习高一数学寒假精品衔接讲义练习人教B版必修第三册docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。


1.了解向量数量积的物理意义，重点培养数学抽象核心素养．
2．掌握向量数量积的定义、理解其几何意义，重点提升直观想象、数学运算核心素养．
3.掌握平面向量数量积的运算律，并要注意运算律的适用范围以及与实数乘法运算律的区别，重点培养数学抽象核心素养．
4.会应用向量数量积的运算律进行相关的计算或证明等问题，重点提升数学运算核心素养．
5.掌握平面向量数量积的坐标表示，会用向量的坐标形式求数量积，重点培养数学运算核心素养．
6．能根据向量的坐标计算向量的模、夹角及判定两个向量垂直，进一步提升数学运算、逻辑推理核心素养．
【知识导航】
知识点一 两个向量的夹角
1．设非零向量a，b，能否把a，b平移到共同起点？
提示：能．
2．△ABC为正三角形，向量eq \(AB,\s\up6(→))与eq \(AC,\s\up6(→))的夹角是多少？向量eq \(AB,\s\up6(→))与eq \(BC,\s\up6(→))的夹角又是多少？
提示：60°，120°.
知识点二 向量数量积的定义
如图，在力F的作用下，木块在水平方向上移动了5 m，若F＝3 N.
(1)则力F做的功是多少？
(2)力做功的大小与哪些量有关？
提示：(1)3×5×cs 30°＝eq \f(15 \r(3),2) (J)．
(2)与力的大小、位移的大小及它们的夹角有关．
1．平面向量数量积的定义
已知两个非零向量a与b，则把数量|a||b|cs 〈a，b〉称为a与b的数量积(或内积)，记作a·b，即a·b＝|a||b|cs〈a，b〉．
规定零向量与任一向量的数量积为0．
2．向量数量积的性质
(1)|a·b|≤|a||b|
(2)a·a＝|a|2，即|a|＝ eq \r(a·a)
(3)a⊥b⇔a·b＝0
(4)cs〈a，b〉＝eq \f(a·b,|a||b|)
(5)当a与b同向时a·b＝|a||b|
当a与b反向时a·b＝－|a||b|
[点拨]
1．两向量的数量积，其结果是数量，而不是向量，它的值等于两向量的模与两向量夹角余弦值的乘积，其符号由夹角的余弦值来决定．
2．两个向量的数量积记作a·b，千万不能写成a×b的形式．
向量的投影与向量数量积的几何意义
在平面直角坐标系中
1．过点A(1，1)，点B(3，2)向x轴引垂线、垂足分别为A1、B1，则向量eq \(AB,\s\up6(→))在x轴方向上的投影及投影的数量分别是什么？
提示：eq \(A1B1,\s\up6(→))；|eq \(A1B1,\s\up6(→))|＝2.
2．过点C(－1，1)向x轴引垂线，垂足为C1，则向量eq \(OC,\s\up6(→))在x轴上的投影及投影的数量分别是什么？二者有什么联系？
提示：向量eq \(OC1,\s\up6(→))、－|eq \(OC1,\s\up6(→))|＝－1；投影是一个向量，而投影的数量与投影的长度和向量eq \(OC,\s\up6(→))与eq \(Ox,\s\up6(→))的夹角有关．当〈eq \(OC,\s\up6(→))，eq \(Ox,\s\up6(→))〉为钝角时，向量eq \(OC,\s\up6(→))在x轴上的投影的数量为－|eq \(OC1,\s\up6(→))|.
1．投影：向量b在a上的投影的数量|b|cs 〈a，b〉；
向量a在b上的投影的数量|a|cs 〈a，b〉．
2．a·b的几何意义
a·b等于a在向量b上的投影的数量与b的模的乘积．
[拓展]
对向量的投影的数量的几点说明
(1)设非零向量a与b的夹角是θ，则a在b方向上的投影的数量也可以写成eq \f(a·b,|b|)，它的符号取决于角θ的余弦值．
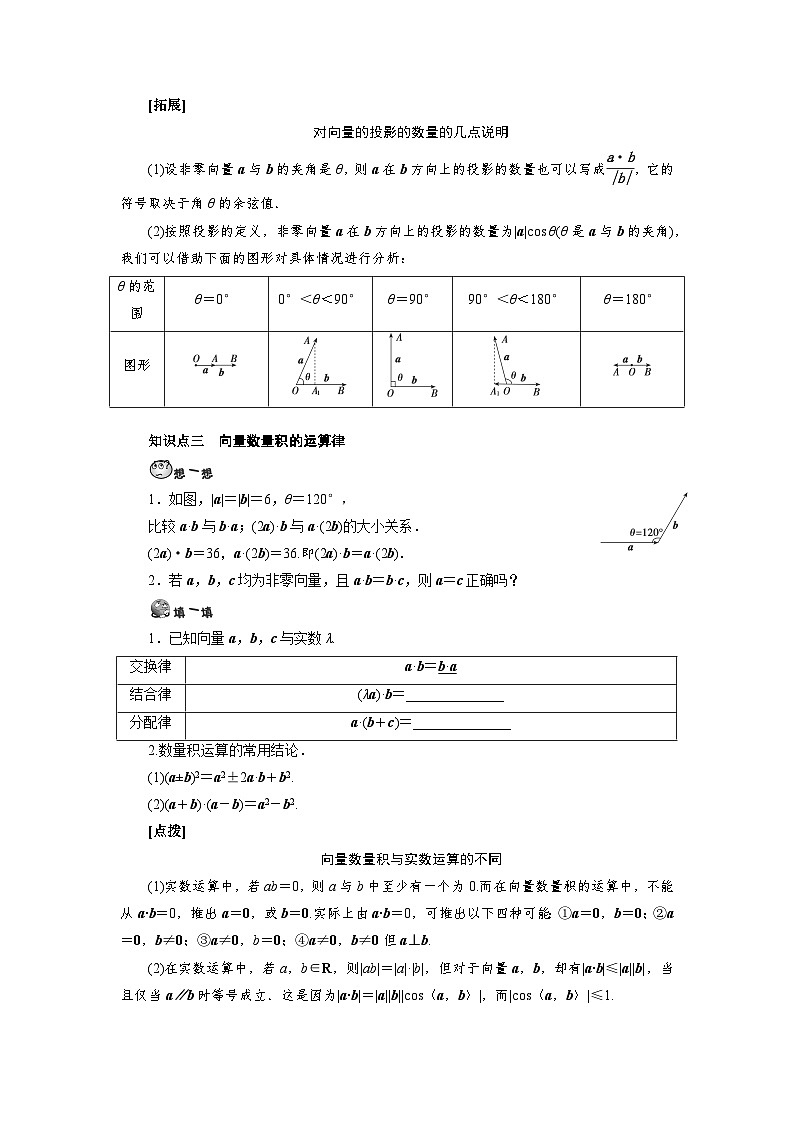
(2)按照投影的定义，非零向量a在b方向上的投影的数量为|a|cs θ(θ是a与b的夹角)，我们可以借助下面的图形对具体情况进行分析：
知识点三 向量数量积的运算律
1．如图，|a|＝|b|＝6，θ＝120°，
比较a·b与b·a；(2a)·b与a·(2b)的大小关系．
提示：a·b＝b·a＝18.
(2a)·b＝36，a·(2b)＝36.即(2a)·b＝a·(2b)．
2．若a，b，c均为非零向量，且a·b＝b·c，则a＝c正确吗？
提示：不正确．因为a·b＝c·b表示向量a，c在b上投影的数量相等，如图并不能说明a＝c.
1．已知向量a，b，c与实数λ.
2.数量积运算的常用结论．
(1)(a±b)2＝a2±2a·b＋b2.
(2)(a＋b)·(a－b)＝a2－b2.
[点拨]
向量数量积与实数运算的不同
(1)实数运算中，若ab＝0，则a与b中至少有一个为0.而在向量数量积的运算中，不能从a·b＝0，推出a＝0，或b＝0.实际上由a·b＝0，可推出以下四种可能：①a＝0，b＝0；②a＝0，b≠0；③a≠0，b＝0；④a≠0，b≠0但a⊥b.
(2)在实数运算中，若a，b∈R，则|ab|＝|a|·|b|，但对于向量a，b，却有|a·b|≤|a||b|，当且仅当a∥b时等号成立．这是因为|a·b|＝|a||b||cs〈a，b〉|，而|cs〈a，b〉|≤1.
(3)实数运算满足消去律，即若bc＝ca，c≠0，则有b＝a.在向量数量积的运算中，若a·b＝b·c(b≠0)，则只能得到向量a，c在向量b方向上的投影的数量相同，不能得到a＝c.
如图，虽然a·b＝b·c，但a≠c.
知识点四 向量的坐标与向量的数量积
已知两个向量a＝(x1，y1)，b＝(x2，y2)．
(1)若i，j是两个互相垂直且分别与x轴、y轴的正半轴同向的单位向量，则a，b如何用i，j表示？
(2)|a|，|b|分别用坐标怎样表示？
(3)能用a，b的坐标表示a·b吗？
提示：(1)a＝x1i＋y1j，b＝x2i＋y2j.
(2)|a|＝ eq \r(（x1i＋y1j）2)＝ eq \r(xeq \\al(2,1)＋yeq \\al(2,1))；
|b|＝ eq \r(（x2i＋y2j）2)＝ eq \r(xeq \\al(2,2)＋yeq \\al(2,2)).
(3)a·b＝(x1i＋y1j)·(x2i＋y2j)
＝x1x2i2＋(x1y2＋x2y1)i·j＋y1y2j2
＝x1x2＋y1y2.
1．平面向量数量积的坐标表示
若a＝(x1，y1)，b＝(x2，y2)，则a·b＝x1x2＋y1y2．
2．两个向量垂直的坐标表示
设两个非零向量a＝(x1，y1)，b＝(x2，y2)，则a⊥b⇔x1x2＋y1y2＝0．
3．三个重要公式
(1)向量模的公式：设a＝(x1，y1)，则|a|＝ eq \r(xeq \\al(2,1)＋yeq \\al(2,1))．
(2)两点间的距离公式：若A(x1，y1)，B(x2，y2)，则|eq \(AB,\s\up6(→))|＝ eq \r(（x2－x1）2＋（y2－y1）2)．
(3)向量的夹角公式：设两非零向量a＝(x1，y1)，b＝(x2，y2)，a与b的夹角为θ，则cs θ＝eq \f(x1x2＋y1y2,\r(xeq \\al(2,1)＋yeq \\al(2,1))· \r(xeq \\al(2,2)＋yeq \\al(2,2))) .
[点拨]
1．公式a·b＝|a||b|cs〈a，b〉与a·b＝x1x2＋y1y2都是用来求两向量的数量积的，没有本质区别，只是书写形式上的差异，两者可以相互推导．
2．向量垂直的坐标表示与向量平行的坐标表示不能混淆，可以从平行与垂直的定义来理解．设向量a＝(x1，y1)，b＝(x2，y2)．若a∥b，则x2y1－x1y2＝0.垂直则是从数量积的角度理解，若a⊥b，则a·b＝0，即x1x2＋y1y2＝0.
【知识预习】
考点一：向量数量积的概念
1．已知向量，在方向上的投影向量为，则（ ）
A．4B．8C．D．
【答案】C
【详解】由得，根据在方向上的投影向量为，可知在方向上的投影为，故根据数量积的几何意义，等于与在方向上的投影的乘积，故，
故选：C
2．已知，，与的夹角为，则（ ）
A．B．C．D．
【答案】A
【详解】.
故选：A.
3．正的边长为1，则（ ）
A．B．C．D．
【答案】B
【详解】．
故选：B．
4．如图，在菱形ABCD中，若，则（ ）
A．8B．C．4D．
【答案】B
【详解】解：，因为四边形ABCD为菱形，所以，且，所以，
所以.
故选：B
5．已知，，向量在方向上投影是4，则为（ ）
A．12B．8C．-8D．2
【答案】A
【详解】解：设两个向量的夹角为，由题意已知，，
向量在方向上投影是4，则，
所以；
故选：A.
考点二：向量数量积的运算率
6．已知，，，则与的夹角是（ ）
A．30°B．60°C．120°D．150°
【答案】C
【详解】，
因为，
所以，
与的夹角是120°.
故选：C
7．已知向量满足，则与的夹角为（ ）
A．30°B．60°C．120°D．150°
【答案】B
【详解】解：因为，所以，
设与的夹角为，则，
因为，
所以，
故选：B.
8．若夹角为的非零向量，满足且，则（ ）
A．1B．C．2D．3
【答案】C
【详解】因为，所以，即，所以，将代入得.
故选：C.
9．已知，，则（ ）
A．B．C．D．
【答案】A
【详解】由已知可得.
故选：A.
10．已知，，与的夹角为，那么（ ）
A．4B．3C．2D．
【答案】D
【详解】.
故选：D.
考点三：向量数量积的坐标运算
11．已知向量，且，则的值是（ ）
A．B．C．3D．
【答案】C
【详解】由于，所以.
故选：C
12．已知向量，则（ ）
A．B．C．D．
【答案】C
【详解】，则，所以C正确.
故选：C.
13．已知向量，且，则（ ）
A．B．1C．D．2
【答案】B
【详解】，，
由于，
所以，
解得：
故选：B
14．已知向量，点，，则向量在上的投影向量的模长为（ ）
A．B．C．D．
【答案】D
【详解】，故在上的投影向量的模长为
.
故选：D
15．已知，，则（ ）
A．B．1C．D．
【答案】B
【详解】∵，
所以，
由，
所以.
故选：B.
【对点训练】
一、单选题
1．已知向量，，且，则（ ）
A．B．C．D．
【答案】A
【详解】由题意，解得，故.
故选：A
2．已知平面向量满足，若，则（ ）
A．2B．3C．4D．5
【答案】B
【详解】由得，
由得，即
故选：B
3．已知向量，，则与的夹角为（ ）
A．B．C．D．
【答案】C
【详解】解：，因为，所以，
故选：C
4．已知平面向量的夹角为，且，则（ ）
A．4B．4C．8D．8
【答案】C
【详解】因为平面向量的夹角为，且，
所以，
故选：C
5．设向量，，则在上的投影的数量为（ ）
A．1B．2C．1D．2
【答案】B
【详解】因为，，
所以在上的投影的数量为
，
故选：B
6．设非零向量，若，则的取值范围为（ ）
A．B．C．D．
【答案】B
【详解】解：由题意
，
，
，
，
故选：B.
7．已知，，则（ ）
A．B．C．D．
【答案】A
【详解】因为，，
所以，
所以，
故选：A
8．设，向量，且，则等于（ ）
A．B．C．3D．4
【答案】B
【详解】由知：且，则，可得，即，
由知：，可得，即，
所以，故.
故选：B
二、多选题
9．设向量，，则 （ ）
A．B．
C．D．与的夹角为
【答案】CD
【详解】由题意，，，
则 ， ，故A错误；
易知，由，
所以与不平行，故B错误；
又 ，即，故C正确；
因为 ，
又 ，所以与的夹角为，故D正确．
故选：CD．
10．向量是近代数学中重要和基本的概念之一，它既是代数研究对象，也是几何研究对象，是沟通代数与几何的桥梁若向量，满足，，则（ ）
A．B．与的夹角为
C．D．在上的投影向量为
【答案】BC
【详解】，,
,解得,故A错误
,，
由于，与的夹角为，故B正确,
,故C正确
在上的投影向量为，故D错误,
故选：BC
三、填空题
11．已知向量，，若与的夹角为锐角，则的取值范围为___________．
【答案】且.
【详解】由得，，.
由已知得，，所以，即，且不共线.
则，.
又不共线，则.
所以，的取值范围为且.
故答案为：且.
12．已知向量满足，，与的夹角为，则在上的投影为________．
【答案】
【详解】解：由于，，与的夹角为，则
则在上的投影为：.
故答案为：.
四、解答题
13．已知与的夹角为．
(1)求的值；
(2)设，求的夹角．
【答案】(1)(2)
【详解】（1）由已知，得：，
∴，
∴；
（2）∵，
，
∴，
由（1）得：，
∴，
∵，∴.
14．已知向量.
(1)已知，求向量与的夹角；
(2)若，求实数的值.
【答案】(1)(2)或
【详解】（1）因为，所以，
故，
因为，所以向量与的夹角；
（2），
，
由于，
所以，
解得：或，
从而或.
15．已知平面向量，，.
(1)若，求；
(2)若与的夹角为锐角，求x的取值范围.
【答案】(1)2或；(2)
【详解】（1）由题意得：，解得：或，
当时，，所以；
当时，，
所以；
（2）因为与的夹角为锐角，
所以，且与不同向共线，
即，
解得：，且，
综上：x的取值范围是.
【提升作业】
一、单选题
1．已知，，则（ ）
A．1B．C．2D．或2
【答案】C
【详解】因为，
所以，.
故选：C.
2．已知向量与向量的夹角为60°，，，则（ ）
A．20B．10C．D．
【答案】B
【详解】因向量与向量的夹角为60°，，，
所以，B正确.
故选：B
3．已知向量满足，且，则夹角为（ ）
A．B．C．D．
【答案】A
【详解】设夹角为，，即，.
故选：A
4．已知向量，，，且，则实数m的值为（ ）
A．B．C．D．
【答案】A
【详解】，由可得，
解得．
故选：A．
5．已知平面向量是非零向量，，夹角​，则向量​在向量​方向上的投影为（ ）
A．​B．1C．​D．2
【答案】A
【详解】向量​在向量​方向上的投影为.
故选：A
二、填空题
6．已知，，向量在上的投影向量为__.
【答案】
【详解】向量在上的投影向量为.
故答案为：
7．已知向量满足，则与的夹角为_______________．
【答案】
【详解】，
，
设与的夹角为，
，
因为，
所以，
故答案为：
三、解答题
8．已知，，.
(1)求 与 的夹角 ；
(2)求 与 的夹角的余弦值．
【答案】(1)；(2).
【详解】（1）由已知，得，
因为，所以.
又，
所以cs，
因为，所以.
（2）因为，所以，
因为，所以.
所以.
9．已知向量，．
(1)求；
(2)若向量与互相垂直，求的值．
【答案】(1)1(2)
【详解】（1）由，，
.
（2）若向量与互相垂直，
则，
所以．
10．如图，在中，，为边的中点．设向量，向量，求：
(1)；
(2)求．
【答案】(1)(2)
【详解】（1），
.
（2）.
定义
已知两个非零向量a和b，作eq \(OA,\s\up6(→))＝a，eq \(OB,\s\up6(→))＝b，则∠AOB＝θ称为向量a与b的夹角.
范围
〈a，b〉∈[0，π]，〈a，b〉＝〈b，a〉
特例
θ＝0
a与b同向
θ＝π
a与b反向
θ＝eq \f(π,2)
a与b垂直，记作a⊥b，规定0与任意向量垂直
θ的范围
θ＝0°
0°＜θ＜90°
θ＝90°
90°＜θ＜180°
θ＝180°
图形
交换律
a·b＝b·a
结合律
(λa)·b＝a·(λb)＝λ(a·b)
分配律
a·(b＋c)＝a·b＋a·c