专项17.8 勾股定理之垂美四边形模型 2024年鲁教版（五四制）九年级数学专题培训

这是一份专项17.8 勾股定理之垂美四边形模型 2024年鲁教版（五四制）九年级数学专题培训，共6页。试卷主要包含了定义等内容，欢迎下载使用。

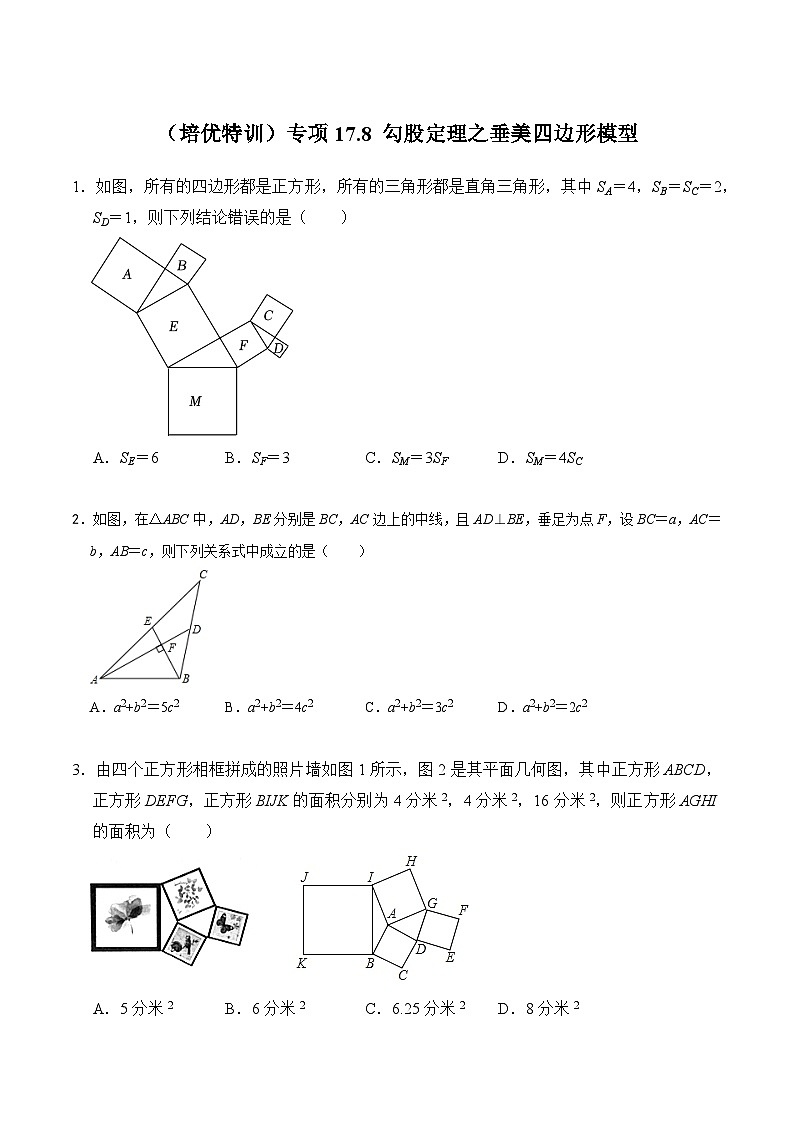
A．SE＝6B．SF＝3C．SM＝3SFD．SM＝4SC
2．如图，在△ABC中，AD，BE分别是BC，AC边上的中线，且AD⊥BE，垂足为点F，设BC＝a，AC＝b，AB＝c，则下列关系式中成立的是（ ）
A．a2+b2＝5c2B．a2+b2＝4c2C．a2+b2＝3c2D．a2+b2＝2c2
3．由四个正方形相框拼成的照片墙如图1所示，图2是其平面几何图，其中正方形ABCD，正方形DEFG，正方形BIJK的面积分别为4分米2，4分米2，16分米2，则正方形AGHI的面积为（ ）
A．5分米2B．6分米2C．6.25分米2D．8分米2
4．（2022秋·福建宁德·八年级校考阶段练习）对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD=2，，则AB2+CD2=________．
5．已知点P是矩形ABCD内的一点，且PA＝2，PB＝3，PC＝4，则PD＝ ．
6．（2023春·浙江湖州·八年级统考期末）定义：对角线垂直的四边形叫做“对垂四边形”．如图，在“对垂四边形”中，对角线与交于点O，．若点E、F、G、H分别是边、、、的中点，且四边形是“对垂四边形”，则四边形的面积是 ．
7．（2022春·山东聊城·八年级校考期中）如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
(1)概念理解：如图2，在四边形ABCD中，AB＝AD，CB＝CD，问四边形ABCD是垂美四边形吗？请说明理由；
(2)性质探究：经探究发现，垂美四边形ABCD两组对边AB，CD与BC，AD之间有这样的数量关系：AB2+CD2＝AD2+BC2，请写出证明过程；（先画出图形，写出已知，求证）
(3)问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG和GE．已知AC＝4，AB＝5，求GE长．
8.（★★★★★）数学活动∶图形的变化
问题情境∶如图1，△ABC为等腰直角三角形，∠ACB=90º，E是AC边上的一个动点(点E与A，C不重合），以CE为边在△ABC外作等腰直角△ECD，∠ECD=90°，连接 BE，AD.猜想线段 BE，AD 之间的关系.
（1）独立思考∶请直接写出线段 BE，AD 之间的关系.
（2）合作交流∶“希望”小组受上述问题的启发，将图1中的等腰直角△ECD绕着点C顺时针方向旋转至如图2的位置，BE交AC于点H,交AD于点O.
（1）中的结论是否仍然成立?请说明理由.
（3）拓展延伸∶“科技”小组将⑵中的等腰直角△ABC改为Rt△ABC，∠ACB=90°，AC=8，BC=6，将等腰直角△ECD改为 Rt△ECD，∠ECD=90°，CD=4，CE=3.试猜想 BD²＋AE²是否为定值，结合图3说明理由.

9．（2023·广东九年级课时练习）小明学习了特殊的四边形后，对特殊四边形的探究产生了兴趣，发现另外一类特殊四边形，如图1，我们把两条对角线互相垂直的四边形叫做垂美四边形．
(1)概念理解：在平行四边形、矩形、菱形、正方形中，一定是垂美四边形的是______．
(2)性质探究：通过探究，直接写出垂美四边形ABCD的面积S与两条对角线AC、BD之间的数量关系：______．
(3)问题解决：如图2，分别以的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结BG、CE交于点N，CE交AB于点M，连结GE．①求证：四边形BCGE为垂美四边形；
②已知，，则四边形BCGE的面积为______．
10．如图，我把对角线互相垂直的四边形叫做“垂美四边形”．
（1）性质探究：如图1．已知四边形ABCD中，AC⊥BD，垂足为O，求证：AB2+CD2＝AD2+BC2．
（2）解决问题：已知AB＝5，BC＝4，分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP．
①如图2，当∠ACB＝90°，连接PQ，求PQ；
②如图3，当∠ACB≠90°，点M、N分别是AC、AP中点连接MN．若MN＝2，则S△ABC＝ ．
11．（2023春·江西赣州·八年级统考期末）如图，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图，在四边形中，，，问四边形是垂美四边形吗？请说明理由．
（2）性质探究：试探究垂美四边形两组对边，与，之间的数量关系，写出证明过程（先画出图形）
（3）问题解决：如图，分别以的直角边和斜边为边向外作正方形和正方形，连接，，已知，，求的长．
12（2023春•越秀区校级期中）如图1，对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：给出下列图形：①平行四边形；②矩形；③菱形；④正方形．其中一定是“垂美四边形”的是 （填序号）；
（2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥BD．求证：AB2+CD2＝AD2+BC2；
（3）解决问题：如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE．已知AC＝，AB＝3．
①请问四边形CGEB是垂美四边形吗？并说明理由；
②求GE的长．