山东省济南市莱芜区2023-2024学年八年级上学期期末数学试卷（五四学制）

这是一份山东省济南市莱芜区2023-2024学年八年级上学期期末数学试卷（五四学制），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．分解因式4x2﹣y2的结果是（ ）
A．（4x+y）（4x﹣y）B．4（x+y）（x﹣y）
C．（2x+y）（2x﹣y）D．2（x+y）（x﹣y）
2．下列分式中是最简分式的是（ ）
A．B．
C．D．
3．某校准备从甲、乙、丙、丁四个科创小组中选出一组，参加区青少年科技创新大赛，表格反映的是各组平时成绩的平均数（单位：分）及方差s2，如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是（ ）
A．甲B．乙C．丙D．丁
4．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
A．B．C．D．
5．在对一组样本数据进行分析时，小华列出了方差的计算公式S2＝，由公式提供的信息，下列说法错误的是（ ）
A．样本容量是5B．样本的中位数是4
C．样本的平均数是3.8D．样本的众数是4
6．若一个多边形的内角和是1080度，则这个多边形的边数为（ ）
A．6B．7C．8D．10
7. 正方形具有而菱形不一定具有的性质是 ( )
A.对角线相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.四条边相等
8..菱形的一个内角为60°，一边长为2，则它的面积为：（ ）
A． B. C.2 D.4
9.．以三角形的三个顶点及三边中点为顶点的平行四边形共有（ ）
A．1个 B．2个 C．3个 D．4个
10. 如图，△ABC周长为a，以它的各边的中点为顶点作△A1B1C1，再以△AB1C1各边的中点为顶点作△A2B2C2，再以△AB2C2各边的中点为顶点作△A3B3C3，…如此下去，则△AnBnCn的周长为（ ）
A. aB. aC. aD. a
二、填空题
11. 如果关于x的方程有增根，那么m的值为________．
12. 如果关于x的多项式是一个完全平方式，那么b的值为__．
13. 已知一组数据x1，x2，x3的平均数和方差分别为5和2，则数据x1+1，x2+1，x3+1的平均数是__，标准差是__．
14. 如图，在中，，的平分线交于E，则的长为______．
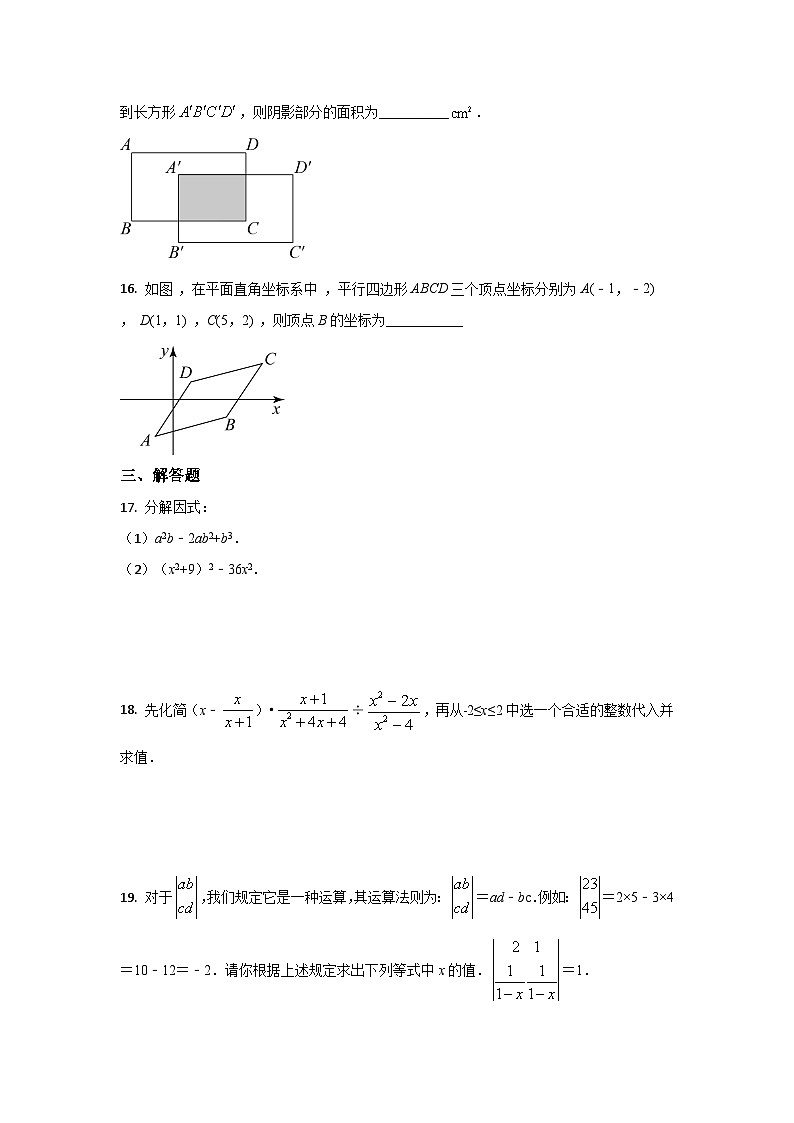
15. 如图，将长为5cm，宽为3cm的长方形先向右平移2cm，再向下平移1cm，得到长方形，则阴影部分的面积为__________．
16. 如图 ，在平面直角坐标系中 ，平行四边形ABCD三个顶点坐标分别为A(﹣1，﹣2) ， D(1，1) ，C(5，2) ，则顶点B的坐标为___________
三、解答题
17. 分解因式：
（1）a2b﹣2ab2+b3．
（2）（x2+9）2﹣36x2．
18. 先化简（x﹣）•÷，再从﹣2≤x≤2中选一个合适的整数代入并求值．
19. 对于，我们规定它是一种运算，其运算法则为：＝ad﹣bc．例如：＝2×5﹣3×4＝10﹣12＝﹣2．请你根据上述规定求出下列等式中x的值．＝1．
20. 为有效控制新型冠状病毒的传染，目前，国家正全面推开新冠疫苗的免费接种工作．某社区为了解其辖区内居民的接种情况，随机抽查了一部分居民进行问卷调查，把调查的结果分为（已经接种）、（准备接种）、（观望中）、（不接种）四种类别，并绘制了下面两幅不完整的统计图，请根据图中提供的信息解答下列问题：
（1）此次抽查的居民人数为______人；
（2）请补全条形统计图，同时求出类别所在扇形的圆心角度数；
（3）若该社区共有居民4000人，请你估计该社区已接种新冠疫苗的居民约有多少人？
21. 在边长为1个单位长度的小正方形组成的网格中，建立平面直角坐标系，△ABC的位置如图所示，先作△ABC关于原点O成中心对称的△A1B1C1，再把△A1B1C1向上平移4个单位长度得到△A2B2C2．
（1）画出△A1B1C1和△A2B2C2．
（2）△A2B2C2与△ABC关于某点成中心对称，直接写出对称中心的坐标________；
（3）已知P为x轴上一点．若△ABP的面积为3，直接写出点P的坐标________；
22. 为做好新冠疫情的防控工作，某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元，该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液．
（1）求甲、乙两种消毒液的零售价分别是每桶多少元？
（2）由于疫情防控进入常态化，该单位需再次购买两种消毒液共300桶，且甲种消毒液的桶数不少于乙种消毒液桶数的，由于购买量大，甲、乙两种消毒液分别获得了20元/桶，15元/桶的批发价．求甲种消毒液购买多少桶时，所需资金总额最少？最少总金额是多少元？
23. 已知是等边三角形，点在射线上（与点，不重合），点关于直线的对称点为点，连接，，，．
（1）如图1，当点为线段的中点时，求证：是等边三角形；
（2）当点在线段的延长线上时，连接，为线段的中点，连接．根据题意在图2中补全图形，用等式表示线段与的数量关系，并证明．
甲
乙
丙
丁
6
7
7
6
s2
1
1.1
1
1.6