甘肃省平凉市静宁县2023-2024学年数学八上期末监测试题含答案

这是一份甘肃省平凉市静宁县2023-2024学年数学八上期末监测试题含答案，共8页。试卷主要包含了考生必须保证答题卡的整洁，下列计算正确的是，如图，△ABC的面积计算方法是等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
考生请注意：
1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。
2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。
3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。
一、选择题（每题4分，共48分）
1．已知，如图点A（1，1），B（2，﹣3），点P为x轴上一点，当|PA﹣PB|最大时，点P的坐标为（ ）
A．（﹣1，0）B．（，0）C．（，0）D．（1，0）
2．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）
A．6B．8C．10D．12
3．已知直角三角形的两条边长分别是3和5，那么这个三角形的第三条边的长( )
A．4B．16C．D．4或
4．下列四个图形中，既是轴对称图形，又是中心对称图形的是( )
A．B．C．D．
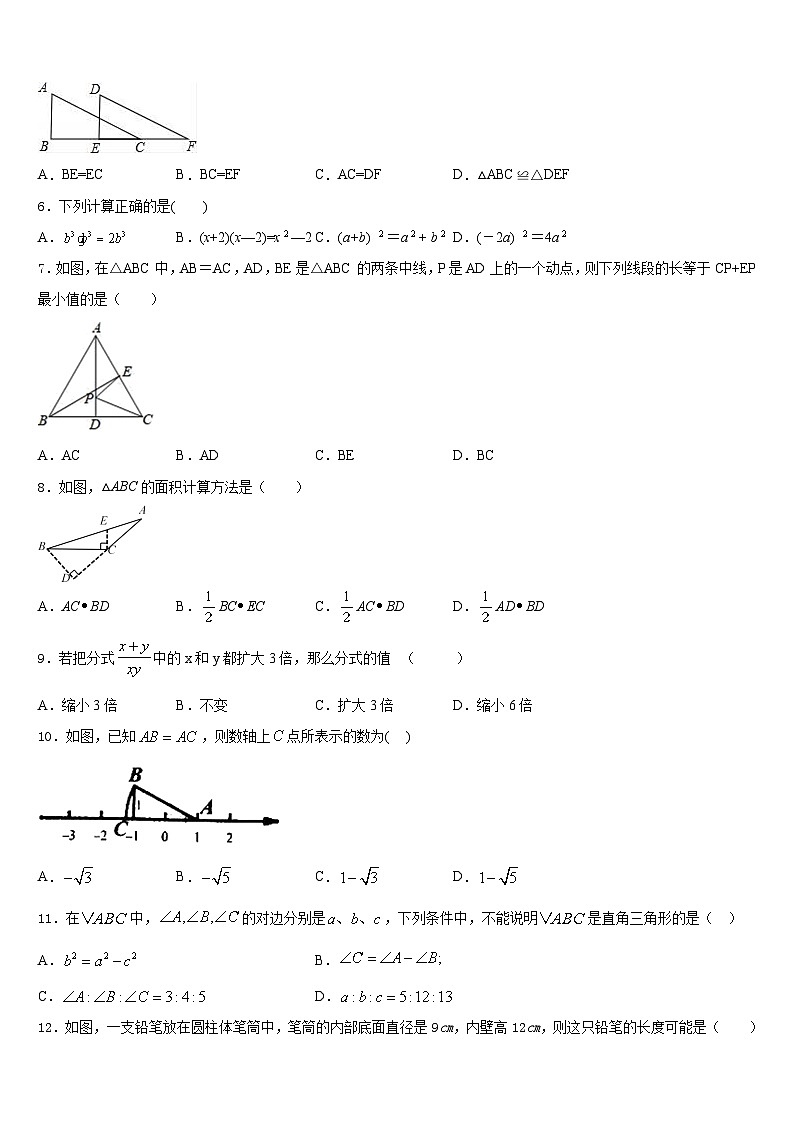
5．如图，Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF，则下列结论中，错误的是（ ）
A．BE=ECB．BC=EFC．AC=DFD．△ABC≌△DEF
6．下列计算正确的是( )
A．B．(x+2)(x—2)=x—2C．(a+b) ＝a+ bD．(－2a) ＝4a
7．如图，在△ABC中，AB＝AC，AD，BE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于CP+EP最小值的是（ ）
A．ACB．ADC．BED．BC
8．如图，△ABC的面积计算方法是（ ）
A．ACBDB．BCECC．ACBDD．ADBD
9．若把分式中的x和y都扩大3倍，那么分式的值 （ ）
A．缩小3倍B．不变C．扩大3倍D．缩小6倍
10．如图，已知，则数轴上点所表示的数为( )
A．B．C．D．
11．在中，的对边分别是，下列条件中，不能说明是直角三角形的是（ ）
A．B．
C．D．
12．如图，一支铅笔放在圆柱体笔筒中，笔筒的内部底面直径是9cm，内壁高12cm，则这只铅笔的长度可能是（ ）
A．9cmB．12cmC．15cmD．18cm
二、填空题（每题4分，共24分）
13．如果多边形的每个内角都等于，则它的边数为______.
14．如图在3×3的正方形网格中有四个格点A．B．C．D，以其中一点为原点，网格线所在直线为坐标轴建立直角坐标系，使其余三个点中存在两个点关于一条坐标轴对称，则原点是____点.
15．如图，在中,， ， ，点 在 上，将 沿 折叠,点落在点处，与 相交于点 ，若，则的长是__________.
16．在实数π、、﹣、、0.303003…（相邻两个3之间依次多一个0）中，无理数有_____个．
17．在平面直角坐标系中，点A（2，3）与点B关于x轴对称，则点B的坐标为 ．
18．如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD为∠CAB的角平分线,若CD=3，则DB=____.
三、解答题（共78分）
19．（8分）为了解某中学学生对“厉行勤俭节约，反对铺张浪费”主题活动的参与情况，小卫在全校范围内随机抽取了若干名学生，就某日午饭浪费饭菜情况进行了调查．调查内容分为四组：A．饭和菜全部吃完；B．有剩饭但菜吃完；C．饭吃完但菜有剩余；D．饭和菜都有剩余．根据调查结果，绘制了如下两幅不完整的统计图．
回答下列问题：
（1）扇形统计图中，“B组”所对应的圆心角的度数是_______；
（2）补全条形统计图；
（3）已知该中学共有学生2500人，请估计这日午饭有剩饭的学生人数；若按平均每人剩10克米饭计算，这日午饭将浪费多少千克米饭？．
20．（8分）八（1）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：
（Ⅰ）如图5-1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；
（Ⅱ）如图5-2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.
阅读后1回答下列问题：
（1）方案（Ⅰ）是否可行？说明理由.
（2）方案（Ⅱ）是否可行？说明理由.
（3）方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是 ；若仅满足∠ABD=∠BDE≠90°, 方案（Ⅱ）是否成立？ .
21．（8分）如图，直线与直线交于点A，点A的横坐标为，且直线与x轴交于点B，与y轴交于点D，直线与y轴交于点C．
（1）求点A的坐标及直线的函数表达式；
（2）连接，求的面积.
22．（10分）如图1 ,等腰直角三角形 ABC 中，∠ACB＝90°，CB＝CA，直线 DE 经过点 C，过 A 作 AD⊥DE 于点 D，过 B 作 BE⊥DE 于点 E，则△BEC≌△CDA，我们称这种全等模型为 “K 型全等”．（不需要证明）
（模型应用）若一次函数 y=kx+4（k≠0）的图像与 x 轴、y 轴分别交于 A、B 两点．
（1）如图 2，当 k=－1 时，若点 B 到经过原点的直线 l 的距离 BE 的长为 3，求点 A 到直线 l 的距离 AD 的长；
（2）如图 3，当 k=－ 时，点 M 在第一象限内，若△ABM 是等腰直角三角形，求点
M 的坐标；
（3）当 k 的取值变化时，点 A 随之在 x 轴上运动，将线段 BA 绕点 B 逆时针旋转 90° 得到 BQ，连接 OQ，求 OQ 长的最小值．
23．（10分）某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克，如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完．
（1）该种干果的第一次进价是每千克多少元？
（2）超市销售这种干果共盈利多少元？
24．（10分）先化简，再求值：,其中m=9.
25．（12分）计算:
（1）
（2）先化简，再求值: [(2m+n)(2m-n)+(m+n)2-2(2m2-mn)]÷(-4m)，其中m=1，n=.
26．（12分）一支园林队进行某区域的绿化，在合同期内高效地完成了任务，这是记者与该队工程师的一段对话：
如果每人每小时绿化面积相同，请通过这段对话，求每人每小时的绿化面积．
参考答案
一、选择题（每题4分，共48分）
1、B
2、C
3、D
4、B
5、A
6、D
7、C
8、C
9、A
10、D
11、C
12、D
二、填空题（每题4分，共24分）
13、1
14、B点
15、
16、3
17、（2，－3）
18、1
三、解答题（共78分）
19、（1）12°；（2）见解析；（3）这日午饭有剩饭的学生人数是150人，将浪费1.5千克米饭
20、（1）见解析；（2）见解析；（3）∠ABD=∠BDE=90°，成立.
21、 (1) ;(2)1.
22、（1）；（2）点M的坐标为（7,3）或（1,7）或（，）；（3）OQ的最小值为1．
23、（1）该种干果的第一次进价是每千克5元.（2）超市销售这种干果共盈利5820元．
24、
25、（1）－27a10；（2），
26、每人每小时的绿化面积为2.5平方米．