2023-2024学年河北省秦皇岛市青龙满族自治县数学八上期末复习检测模拟试题含答案

这是一份2023-2024学年河北省秦皇岛市青龙满族自治县数学八上期末复习检测模拟试题含答案，共7页。试卷主要包含了已知，的值为等内容，欢迎下载使用。

学校_______ 年级_______ 姓名_______
注意事项
1．考试结束后，请将本试卷和答题卡一并交回．
2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．
3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．
4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．
5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．
一、选择题（每题4分，共48分）
1．下列各组数中，以它们为边的三角形不是直角三角形的是（ ）
A．3，4，5B．5，12，13C．7，24，25D．5，7，9
2．下面四个手机应用图标中是轴对称图形的是( )
A．B．C．D．
3．在矩形（长方形）ABCD中，AB=3，BC=4，若在矩形所在的平面内找一点P，使△PAB，△PBC，△PCD，△PAD都为等腰三角形，则满足此条件的点P共有（ ）个．
A．3 个B．4 个C．5 个D．6 个
4．在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（ ）
A．（﹣1，1） B．（﹣1，﹣2） C．（﹣1，2） D．（1，2）
5．在一组数﹣4，0.5，0，π，﹣，0.1010010001…（相邻两个1之间依次增加1个0）中，无理数有（ ）个．
A．1个B．2个C．3个D．4个
6．已知，的值为（ ）
A．B．C．3D．9
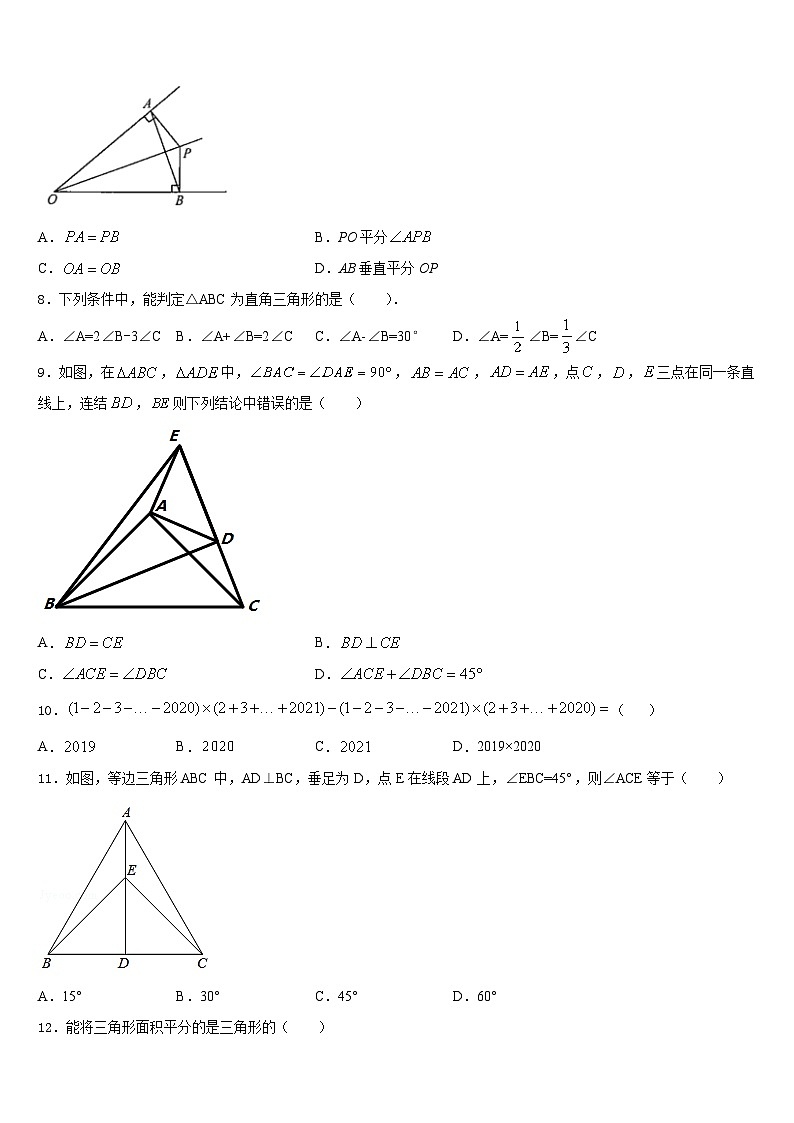
7．如图所示，OP平分，，，垂足分别为A、B．下列结论中不一定成立的是（ ）．
A．B．PO平分
C．D．AB垂直平分OP
8．下列条件中，能判定△ABC为直角三角形的是（ ）．
A．∠A=2∠B-3∠CB．∠A+∠B=2∠CC．∠A-∠B=30°D．∠A=∠B=∠C
9．如图，在，中，，，，点，，三点在同一条直线上，连结，则下列结论中错误的是（ ）
A．B．
C．D．
10．（ ）
A．B．C．D．2019×2020
11．如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（ ）
A．15°B．30°C．45°D．60°
12．能将三角形面积平分的是三角形的（ ）
A．角平分线B．高C．中线D．外角平分线
二、填空题（每题4分，共24分）
13．光的速度约为3×105 km/s,太阳系以外距离地球最近的一颗恒星(比邻星)发出的光需要4年的时间才能到达地球.若一年以3×107 s计算,则这颗恒星到地球的距离是_______km.
14．已知，分别是的整数部分和小数部分，则的值为_______．
15．在平行四边形ABCD 中， BC边上的高为4 ，AB=5 ， ，则平行四边形ABCD 的周长等于______________ ．
16．用科学记数法表示：0.000002018＝_____．
17．已知多项式，那么我们把和称为的因式，小汪发现当或时，多项式的值为1．若有一个因式是（为正数），那么的值为______，另一个因式为______．
18．已知多项式是关于的完全平方式，则________．
三、解答题（共78分）
19．（8分） “a2≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式．例如：x2+4x+5＝x2+4x+4+1＝（x+2）2+1，∵（x+2）2≥0，∴（x+2）2+1≥1，∴x2+4x+5≥1．试利用“配方法”解决下列问题：
（1）填空：x2﹣4x+5＝（x ）2+ ；
（2）已知x2﹣4x+y2+2y+5＝0，求x+y的值；
（3）比较代数式：x2﹣1与2x﹣3的大小．
20．（8分）化简式子（1），并在﹣2，﹣1，0，1，2中选取一个合适的数作为a的值代入求值．
21．（8分）如图，在平面直角坐标系xOy中，一次函数y1=−x+2与x轴、y轴分别相交于点A和点B，直线y2=kx+b(k≠0)经过点C(1，0)且与线段AB交于点P，并把△ABO分成两部分．
(1)求A、 B的坐标；
(2)求△ABO的面积；
(3)若△ABO被直线CP分成的两部分的面积相等，求点P的坐标及直线CP的函数表达式．
22．（10分）建立模型：如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．
实践操作：过点A作AD⊥l于点D，过点B作BE⊥l于点E，求证：△CAD≌△BCE．
模型应用：（1）如图1，在直角坐标系中，直线l1：y=x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l1．求l1的函数表达式．
（1）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，1a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．
23．（10分）在如图所示的方格纸中．
（1）作出关于对称的图形．
（2）说明，可以由经过怎样的平移变换得到？
（3）以所在的直线为轴，的中点为坐标原点，建立直角坐标系，试在轴上找一点，使得最小(保留找点的作图痕迹，描出点的位置，并写出点的坐标)．
24．（10分）如图，中，，，．
（1）用直尺和圆规在边上找一点，使到的距离等于．
（2）是的________线．
（3）计算（1）中线段的长．
25．（12分）如图，点在上，，，，与交于点．
（1）求证：；
（2）若，试判断的形状，并说明理由．
26．（12分）我国著名的数学家赵爽，早在公元3世纪，就把一个矩形分成四个全等的直角三角形，用四个全等的直角三角形拼成了一个关的正方形（如图1），这个矩形称为赵爽弦图，验证了一个非常重要的结论：在直角三角形中两直角边a、b与斜边c满足关系式．称为勾股定理．
（1）爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形（如图2），也能验证这个结论，请你帮助小明完成验证的过程；
（2）如图3所示，，请你添加适当的辅助线证明结论．
参考答案
一、选择题（每题4分，共48分）
1、D
2、C
3、C
4、A
5、B
6、D
7、D
8、D
9、C
10、C
11、A
12、C
二、填空题（每题4分，共24分）
13、3.6×1013
14、
15、12或1
16、2.018×10﹣1．
17、1
18、15或
三、解答题（共78分）
19、（1）﹣2，1；（2）1；（2）x2﹣1＞2x﹣2
20、，1.
21、（1）A(3，0)，B(0，2)；（2）3；（3）P (，)，y=-1x+1
22、实践操作：详见解析；模型应用：（1）y=x+2；（1）A、P、Q可以构成以点Q为直角顶点的等腰直角三角形，a的值为或2．
23、（1）图见解析；（2）可以由向右平移个单位，向下平移个单位得到；（3）点的坐标为(1，0)．
24、（1）画图见解析；（2）平分；（1）1．
25、 (1)详见解析；（2）为等腰直角三角形,理由详见解析.
26、（1）见解析；（2）见解析