

2023-2024学年江苏省滨海县八上数学期末检测模拟试题含答案
展开学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每题4分,共48分)
1.篮球小组共有15名同学,在一次投篮比赛中,他们的成绩如右面的条形图所示,这15名同学进球数的众数和中位数分别是( )
A.6,7B.7,9C.9,7D.9,9
2.三角形的五心在平面几何中占有非常重要的地位,这五心分别是:重心、外心、内心、垂心、旁心,其中三角形的重心是三角形的( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高所在直线的交点
D.三边垂直平分线的交点
3.纳米是长度单位,纳米技术已广泛应用于各个领域,已知1纳米=0.000000001米,某原子的直径大约是2纳米,用科学记数法表示该原子的直径约为( )
A.B.C.D.
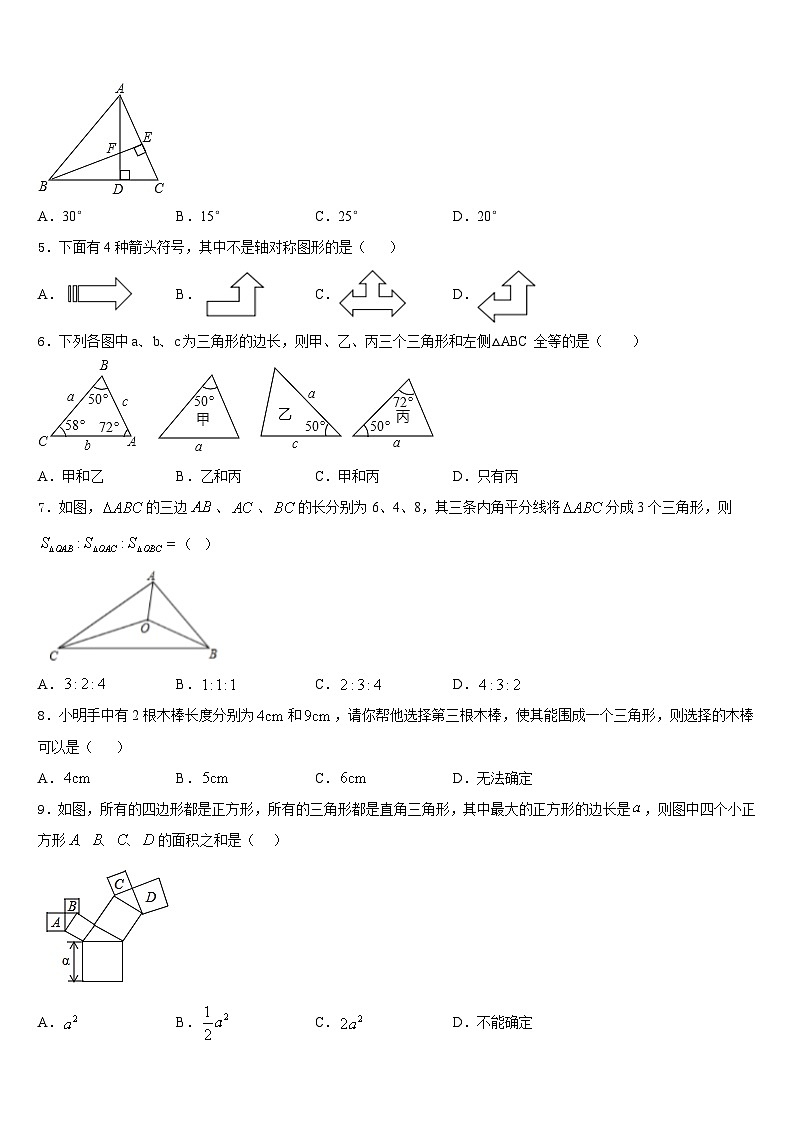
4.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度数为( )
A.30°B.15°C.25°D.20°
5.下面有4种箭头符号,其中不是轴对称图形的是( )
A.B.C.D.
6.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是( )
A.甲和乙B.乙和丙C.甲和丙D.只有丙
7.如图,的三边、、的长分别为6、4、8,其三条内角平分线将分成3个三角形,则( )
A.B.C.D.
8.小明手中有2根木棒长度分别为和,请你帮他选择第三根木棒,使其能围成一个三角形,则选择的木棒可以是( )
A.B.C.D.无法确定
9.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是,则图中四个小正方形的面积之和是( )
A.B.C.D.不能确定
10.如图,已知∠1=∠2,若用“SAS”证明△ACB≌△BDA,还需加上条件( )
A.AD =BCB.BD=ACC.∠D=∠CD.OA=OB
11.下列哪一组数是勾股数( )
A.9,12,13B.8,15,17C.,3,D.12,18,22
12.小明学习了全等三角形后总结了以下结论:
①全等三角形的形状相同、大小相等;
②全等三角形的对应边相等、对应角相等;
③面积相等的两个三角形是全等图形;
④全等三角形的周长相等
其中正确的结论个数是 ( )
A.1B.2C.3D.4
二、填空题(每题4分,共24分)
13.已知,,则的值为____.
14.当a=3,a-b=-1时,a2-ab的值是
15.如图,∠AOB=30°,OP平分∠AOB,PC∥OB交OA于C,PD⊥OB于D.如果PC=8,那么PD等于____________ .
16.如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是_________.
17.如图,是中边上的中线,点分别为和的中点,如果的面积是,则阴影部分的面积是___________.
18.如图,,交于,于,若,则等于_______
三、解答题(共78分)
19.(8分)如图,在中,于.点在边上从点出发,以的速度向终点运动,设点的运动时间为.
(1)求线段的长.
(2)求线段的长.(用含的代数式表示)
(3)求为何值时,点与顶点的连线与的腰垂直.
20.(8分)象山红美人柑橘是我省农科院研制的优质品种,宁波市某种植基地2017年种植“象山红美人”100亩,到2019年“象山红美人”的种植面积达到196亩.
(1)求该基地这两年“象山红美人”种植面积的平均增长率;
(2)市场调查发现,当“象山红美人”的售价为45元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“象山红美人”的平均成本价为33元/千克,若使销售“象山红美人”每天获利3150元,则售价应降低多少元?
21.(8分)在中,,, 是的角平分线.
(1)如图 1,求证:;
(2)如图 2,作的角平分线交线段于点,若,求的面积;
(3)如图 3,过点作于点,点是线段上一点(不与 重合),以为一边,在 的下方作,交延长线于点,试探究线段,与之间的数量关系,并说明理由.
22.(10分)已知:如图,在中,点D在边AC上,BC与DE交于点P,AB=DB,
(1)求证:
(2)若AD=2,DE=5,BE=4,求的周长之和.
23.(10分)如图1,△ABC是边长为4cm的等边三角形,边AB在射线OM上,且OA=6cm,点D从点O出发,沿OM的方向以1cm/s的速度运动,当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.
(1)求证:△CDE是等边三角形(下列图形中任选其一进行证明);
(2)如图2,当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出运动时间t的值;若不存在,请说明理由.
24.(10分)一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
25.(12分)如图,(1)写出顶点C的坐标;
(2)作关于y轴对称的;
(3)若点与点A关于x轴对称,求a-b的值
26.(12分)如图,、两个村子在笔直河岸的同侧,、两村到河岸的距离分别为,,,现在要在河岸上建一水厂向、两村输送自来水,要求、两村到水厂的距离相等.
(1)在图中作出水厂的位置(要求:尺规作图,不写作法,保留作图痕迹);
(2)求水厂距离处多远?
参考答案
一、选择题(每题4分,共48分)
1、C
2、B
3、C
4、D
5、B
6、B
7、A
8、C
9、A
10、B
11、B
12、C
二、填空题(每题4分,共24分)
13、2020
14、-1
15、1
16、30°;
17、1
18、1
三、解答题(共78分)
19、(1);(2)DP=;(3)或.
20、(1)平均增长率为40%;(2)售价应降低5元.
21、(1)见解析;(2)的面积=;(3)若点在上时,,理由见解析;若点在上时,,理由见解析.
22、(1)见解析;(2)1
23、 (1)见解析;(2) 存在,当t=2或14s时,以D、E、B为顶点的三角形是直角三角形.
24、(1) 乙队单独做需要1天完成任务
(2) 甲队实际做了3天,乙队实际做了4天
25、(1)(-2,-1);(2)作图见解析;(1)1
26、(1)详见解析;(2)水厂距离处.
2023-2024学年江苏省滨海县联考九上数学期末达标检测试题含答案: 这是一份2023-2024学年江苏省滨海县联考九上数学期末达标检测试题含答案,共9页。试卷主要包含了若点,已知二次函数,则下列说法,以下事件为必然事件的是等内容,欢迎下载使用。
江苏省盐城滨海县联考2023-2024学年九上数学期末质量跟踪监视模拟试题含答案: 这是一份江苏省盐城滨海县联考2023-2024学年九上数学期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了如果,那么代数式的值是.等内容,欢迎下载使用。
江苏省盐城滨海县联考2023-2024学年八年级数学第一学期期末复习检测模拟试题含答案: 这是一份江苏省盐城滨海县联考2023-2024学年八年级数学第一学期期末复习检测模拟试题含答案,共7页。试卷主要包含了下列分式的变形正确的是,在,,,,中,分式的个数是,若,则 的值为,已知,,则的值为等内容,欢迎下载使用。












