广东省汕头市潮南区2023-2024学年八上数学期末统考试题含答案

这是一份广东省汕头市潮南区2023-2024学年八上数学期末统考试题含答案，共7页。试卷主要包含了要使分式有意义，x的取值应满足等内容，欢迎下载使用。
学校_______ 年级_______ 姓名_______
请考生注意：
1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。
一、选择题(每小题3分,共30分)
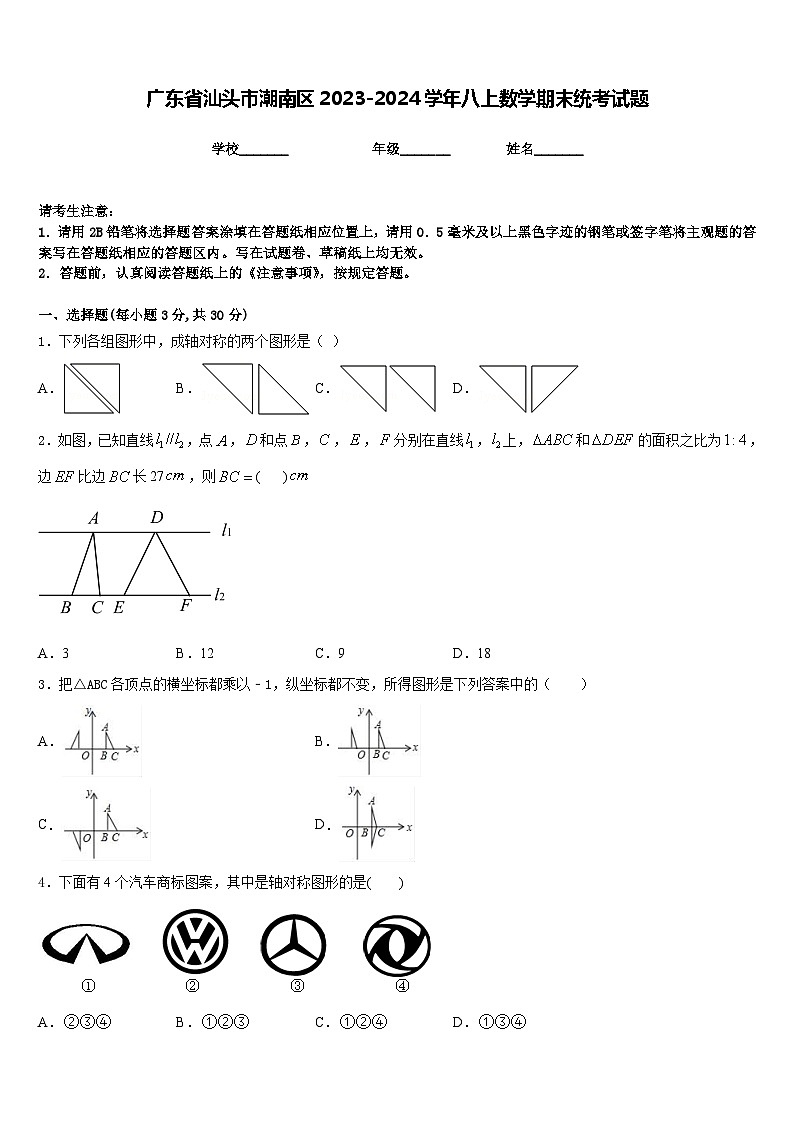
1．下列各组图形中，成轴对称的两个图形是（ ）
A．B．C．D．
2．如图，已知直线，点，和点，，，分别在直线，上，和的面积之比为，边比边长27，则( )
A．3B．12C．9D．18
3．把△ABC各顶点的横坐标都乘以﹣1，纵坐标都不变，所得图形是下列答案中的（ ）
A．B．
C．D．
4．下面有4个汽车商标图案，其中是轴对称图形的是( )
A．B．C．D．
5．若是三角形的三边长，则式子的值（ ）.
A．小于0B．等于0C．大于0D．不能确定
6．若、、为的三边长，且满足，则的值可以为（ ）
A．2B．5C．6D．8
7．如图，已知在△ABC，AB＝AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（ ）
A．AE＝ECB．AE＝BEC．∠EBC＝∠BACD．∠EBC＝∠ABE
8．用反证法证明“三角形的三个外角中至多有一个锐角”，应先假设
A．三角形的三个外角都是锐角
B．三角形的三个外角中至少有两个锐角
C．三角形的三个外角中没有锐角
D．三角形的三个外角中至少有一个锐角
9．已知点 (，3) ，B(，7)都在直线上，则的大小关系为（ ）
A．B．C．D．不能比较
10．要使分式有意义，x的取值应满足（ ）
A．x≠1B．x≠﹣2C．x≠1或x≠﹣2D．x≠1且x≠﹣2
二、填空题(每小题3分,共24分)
11．在中,,,则面积为_______．
12．如图，在中，，，的垂直平分线交于，交于，且，则的长为_______．
13．多项式因式分解为 _________
14．我国是一个水资源贫乏的国家，每一个公民都应自觉养成节约用水的意识和习惯，为提高水资源的利用率，某住宅小区安装了循环用水装置. 经测算，原来天用水吨，现在这些水可多用4天，现在每天比原来少用水________吨.
15．在平面直角坐标系中，点的坐标是，则点关于轴对称的对称点的坐标是__________．
16．如图(1)是长方形纸带， ，将纸带沿折叠图(2)形状，则等于________度．
17．计算：（3×10﹣5）2÷（3×10﹣1）2＝_____．
18．如图所示，在中，，，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则的度数为（________）
三、解答题(共66分)
19．（10分）如图，已知直线l1：y1＝2x+1与坐标轴交于A、C两点，直线l2：y2＝﹣x﹣2与坐标轴交于B、D两点，两直线的交点为P点．
(1)求P点的坐标；
(2)求△APB的面积；
(3)x轴上存在点T，使得S△ATP＝S△APB，求出此时点T的坐标．
20．（6分）在中，是角平分线，．
（1）如图1，是高，，，则 （直接写出结论，不需写解题过程）；
（2）如图2，点在上，于，试探究与、之间的数量关系，写出你的探究结论并证明；
（3）如图3，点在的延长线上，于，则与、之间的数量关系是 （直接写出结论，不需证明）.
21．（6分）（1）计算：
（2）解不等式组
22．（8分）如图，为的高，为角平分线，若.
（1）求的度数；
（2）求的度数；
（3）若点为线段上任意一点，当为直角三角形时，则求的度数.
23．（8分）如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB．
（1）若∠ABC=70°，则∠NMA的度数是 度．
（2）若AB=8cm，△MBC的周长是14cm．
①求BC的长度；
②若点P为直线MN上一点，请你直接写出△PBC周长的最小值．
24．（8分）如图，在直角坐标系中，A（－1，5），B（－3，0），C（－4，3）．
（1）在图中作出△ABC关于y轴对称的图形△A1B1C1；
（2）求△ABC的面积．
25．（10分）如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，点D在边AB上，点E在边AC的左侧，连接AE．
（1）求证：AE＝BD；
（2）试探究线段AD、BD与CD之间的数量关系；
（3）过点C作CF⊥DE交AB于点F，若BD：AF＝1：2，CD＝，求线段AB的长．
26．（10分）如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．
（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的？若存在求出此时点M的坐标；若不存在，说明理由．
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、A
4、B
5、A
6、B
7、C
8、B
9、A
10、D
二、填空题(每小题3分,共24分)
11、60
12、
13、x(x-10)
14、
15、（-3，-5）
16、1
17、．
18、30
三、解答题(共66分)
19、（1）P(﹣1，﹣1)；（2）；（3）T(1，0)或(﹣2，0)．
20、 (1) 11；(2) ∠DEF=(∠C-∠B)，证明见解析；(3) ∠DEF=(∠C-∠B) ，证明见解析
21、（1）（2）
22、（1）26°（2）12°（3）
23、（1）50；（2）①6；②1
24、（1）图见解析；（2）．
25、（1）见解析；（2）BD2+AD2＝2CD2；（3）AB＝2+1．
26、（1）y＝﹣x+6；（2）S△OAC＝12；（3）存在，M的坐标是：M1（1，）或M2（1，5）或M3（﹣1，7）