



清单04 直线与圆的位置关系、圆与圆的位置关系 -2023-2024学年高二数学上学期期末常考题型+易错题(苏教版)
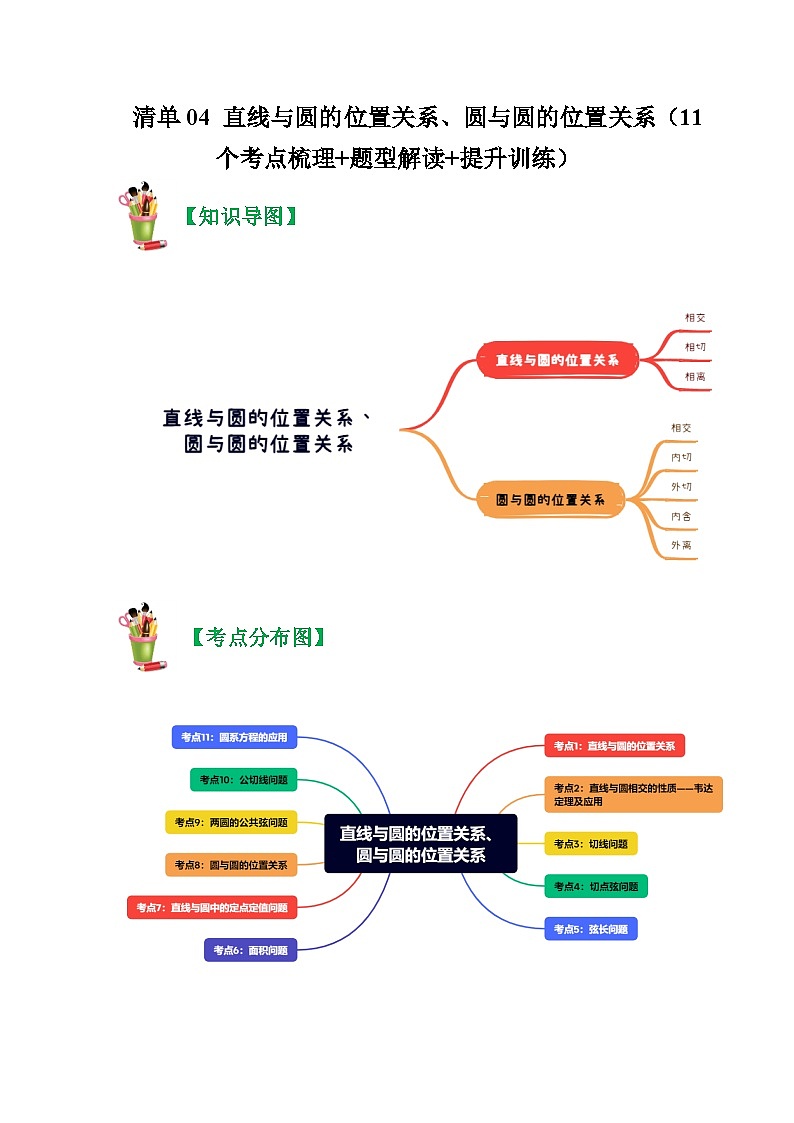
展开【考点分布图】
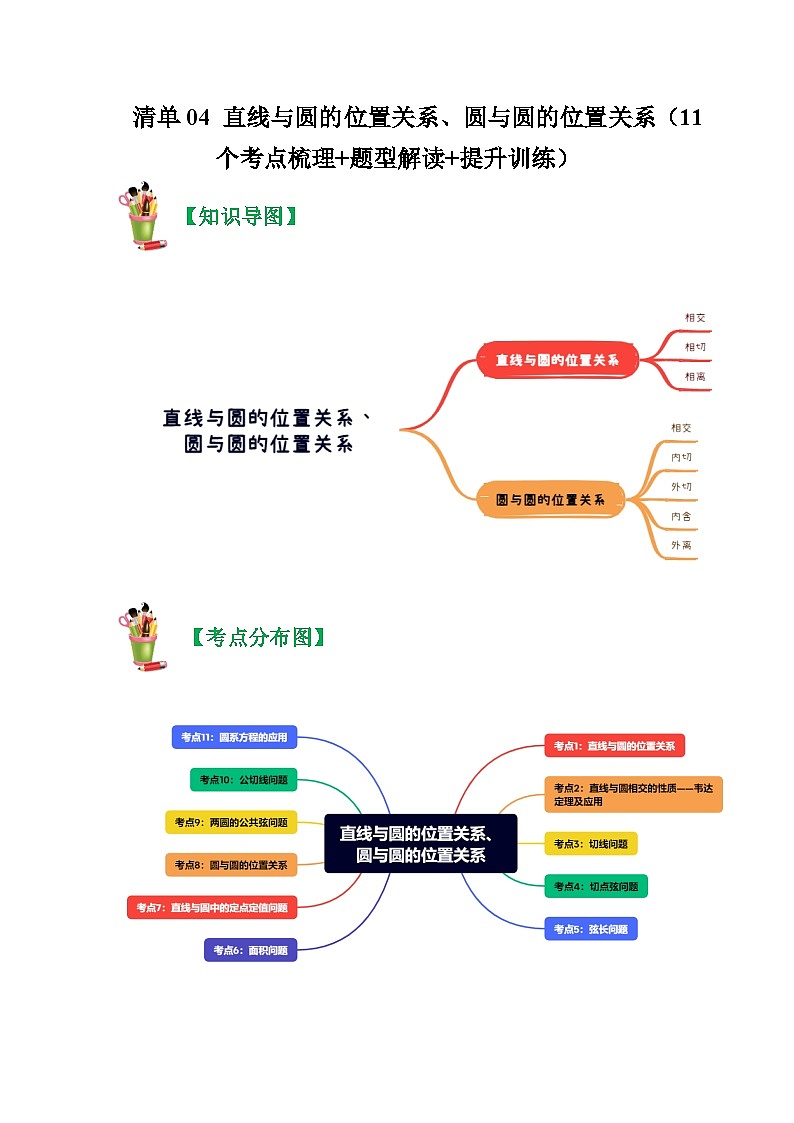
【知识清单】
1、直线与圆的位置关系:
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点.
2、直线与圆的位置关系的判定:
(1)代数法:
判断直线与圆C的方程组成的方程组是否有解.如果有解,直线与圆C有公共点.
有两组实数解时,直线与圆C相交;
有一组实数解时,直线与圆C相切;
无实数解时,直线与圆C相离.
(2)几何法:
由圆C的圆心到直线的距离与圆的半径的关系判断:
当时,直线与圆C相交;
当时,直线与圆C相切;
当时,直线与圆C相离.
3、圆的切线方程的求法
(1)点在圆上,如图.
法一:利用切线的斜率与圆心和该点连线的斜率的乘积等于,即.
法二:圆心到直线的距离等于半径.
(2)点在圆外,则设切线方程:,变成一般式:,因为与圆相切,利用圆心到直线的距离等于半径,解出.
诠释:
因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.
常见圆的切线方程:
(1)过圆上一点的切线方程是;
(2)过圆上一点的切线方程是
.
4、求直线被圆截得的弦长的方法
(1)应用圆中直角三角形:半径,圆心到直线的距离,弦长具有的关系,这也是求弦长最常用的方法.
(2)利用交点坐标:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间的距离公式计算弦长.
(3)利用弦长公式:设直线,与圆的两交点,将直线方程代入圆的方程,消元后利用根与系数关系得弦长:=.
5、圆与圆的位置关系:
(1)圆与圆相交,有两个公共点;
(2)圆与圆相切(内切或外切),有一个公共点;
(3)圆与圆相离(内含或外离),没有公共点.
6、圆与圆的位置关系的判定:
(1)代数法:
判断两圆的方程组成的方程组是否有解.
有两组不同的实数解时,两圆相交;
有一组实数解时,两圆相切;
方程组无解时,两圆相离.
(2)几何法:
设的半径为,的半径为,两圆的圆心距为.
当时,两圆相交;
当时,两圆外切;
当时,两圆外离;
当时,两圆内切;
当时,两圆内含.
7、两圆公共弦长的求法有两种:
方法一:将两圆的方程联立,解出两交点的坐标,利用两点间的距离公式求其长.
方法二:求出公共弦所在直线的方程,利用勾股定理解直角三角形,求出弦长.
8、两圆公切线的条数
与两个圆都相切的直线叫做两圆的公切线,圆的公切线包括外公切线和内公切线两种.
(1)两圆外离时,有2条外公切线和2条内公切线,共4条;
(2)两圆外切时,有2条外公切线和1条内公切线,共3条;
(3)两圆相交时,只有2条外公切线;
(4)两圆内切时,只有1条外公切线;
(5)两圆内含时,无公切线.
9、圆系方程
(1)过直线与圆的交点的圆系方程是
(2)以为圆心的同心圆系方程是:;
(3)与圆同心的圆系方程是;
(4)过同一定点的圆系方程是.
【考点精讲】
考点1:直线与圆的位置关系
例1.(2023·黑龙江哈尔滨·高二黑龙江省哈尔滨市双城区兆麟中学校考期中)已知,则圆与直线的位置关系是( )
A.相切B.相交C.相离D.不确定
例2.(2023·山西太原·高二统考期中)已知直线,圆,则直线l与圆C的位置关系是( )
A.相交B.相切C.相离D.不确定
例3.(2023·河北石家庄·高二石家庄二中校考期中)已知,则圆与直线的位置关系是( )
A.相切B.相交C.相离D.不确定
例4.(2023·江苏无锡·高二校联考期中)若直线与曲线恰有一个公共点,则b的取值范围是( )
A.B.C.D.
例5.(2023·河南商丘·高二商丘市第一高级中学校联考期中)方程有两相异实根,则实数k的取值范围是( )
A.B.
C.D.
例6.(2023·河南信阳·高二统考期中)已知直线l:与圆C:,点,则下列说法不正确的是( )
A.若直线l与圆C相切,则B.若,则直线l与圆C相离
C.若,则直线l与圆C相交D.若点A在直线l上,则直线l与圆C相切
考点2:直线与圆相交的性质——韦达定理及应用
例7.(2023·江苏苏州·高二苏州中学校考期中)如图,圆与x轴交于A、B两点,动直线:与x轴、y轴分别交于点E、F,与圆交于C、D两点.
(1)求中点M的轨迹方程;
(2)设直线、的斜率分别为、,是否存在实数k使得?若存在,求出k的值;若不存在,说明理由.
例8.(2023·云南昆明·高一校考期中)已知圆C:
(1)证明:圆C恒过两个点.
(2)当时,若过点的直线l与圆C交于M,N两点,且,求直线l的斜率.
例9.(2023·广东东莞·高二校联考期中)已知直线:与圆:相交于,不同两点.
(1)求的范围;
(2)设是圆上的一动点(异于,),为坐标原点,若,求面积的最大值.
例10.(2023·山东烟台·高二校联考期中)已知点,,动点P满足,设P的轨迹为C.
(1)求C的轨迹方程;
(2)若过点A的直线与C交于M,N两点,求取值范围.
例11.(2023·甘肃甘南·高二校考期中)已知圆过点,圆心在直线上,且被直线截得的弦长为.
(1)求圆的方程;
(2)若为圆上两个不同的点,为坐标原点,设直线的斜率分别为,当时,求的斜率的取值范围.
例12.(2023·浙江嘉兴·高二校考期中)已知圆,过点的直线与交于点,,且.
(1)求圆的圆心坐标和半径:
(2)求的方程;
(3)设为坐标原点,求的值.
例13.(2023·湖北·高二荆州中学校联考期中)已知圆的半径为2,圆心在轴正半轴上,直线与圆相切.
(1)求圆的方程;
(2)若过点的直线与圆交于不同的两点,,且,为坐标原点,求直线的方程.
考点3:切线问题
例14.(2023·江苏盐城·高二校考期中)圆在点处切线的一般式方程为 .
例15.(2023·广东东莞·高二校考期中)以圆上一点为切点的切线的一般式方程为 .
例16.(2023·浙江·高二校联考期中)过点与圆相切的两条直线的夹角为,则 .
例17.(2023·甘肃武威·高二天祝藏族自治县第一中学校联考期中)过点且与圆C:相切的直线方程为 .
例18.(2023·河南南阳·高二社旗县第一高级中学校联考期中)已知圆:,圆:,过圆上的一点P作圆的一条切线,切点为A,且,则实数m的取值范围是 .
例19.(2023·江苏淮安·高二校考阶段练习)过圆外一直线上一动点P作圆的切线,则切线长最小值为
例20.(2023·四川遂宁·高二四川省蓬溪中学校校考期中)已知圆的圆心在直线上,且与直线和轴都相切,则圆的方程为 .
考点4:切点弦问题
例21.(2023·河北·高二校联考期中)过点作圆:的两条切线,切点分别为,,则直线的方程为 .
例22.(2023·安徽宣城·高三统考期末)过点作圆的两条切线,切点分别为A、B,则直线AB方程是 .
例23.(2023·安徽芜湖·高二期末)在平面直角坐标系中,过点,向圆C:引两条切线,切点分别为,则直线过定点 .
例24.(2023·全国·模拟预测)过直线上一点作圆的两条切线,切点分别为,则直线过定点 .
例25.(2023·广东·高三校联考开学考试)过点作圆的两条切线,切点分别为 、,则直线的方程为 .
例26.(2023·湖南益阳·统考一模)已知直线,若P为l上的动点,过点P作的切线,切点为A、B,当最小时,直线的方程为 .
考点5:弦长问题
例27.(2023·广东东莞·高二校联考期中)已知圆,直线,直线l被圆C截得的弦长为
例28.(2023·广东江门·高二台山市第一中学校考期中)已知直线与圆交于A、B两点,若面积为,则m的值为 .
例29.(2023·广东东莞·高二校考期中)直线与圆相交于两点,则的最小值为 .
例30.(2023·安徽宿州·高二校联考期中)已知直线及直线截圆所得的弦长均为8,则圆的半径是 .
例31.(2023·广东东莞·高二东莞市东华高级中学校考期中)已知直线被圆截得的弦长为2,则的值为 .
例32.(2023·江苏无锡·高二校联考期中)已知圆:,过点的直线被圆截得的弦长为4,则直线的方程为
考点6:面积问题
例33.(2023·湖北黄冈·高二校联考期中)过直线上一点作圆:的两条切线,切点分别为,,则四边形的面积的最小值为 .
例34.(2023·云南昆明·高三昆明市第三中学校考阶段练习)在圆内,过点的最长弦和最短弦分别是和,则四边形的面积为( )
A.B.C.D.
例35.(2023·广东佛山·高二佛山一中校考期中)已知圆的方程为,设该圆过点的最长弦和最短弦分别为和,则四边形面积为( )
A.B.C.D.
例36.(2023·四川成都·高二校考期中)过点引直线与曲线相交于,两点,为坐标原点,当的面积取最大值时,直线的斜率等于( )
A.B.C.D.
例37.(2023·浙江·高二期末)已知圆,圆,若圆的切线交圆于、两点,则面积的取值范围是
A.B.C.D.
例38.(2023·福建莆田·高二校考期中)已知,为圆:的两条互相垂直的弦,且垂足为,则四边形ABCD面积的最大值为( )
A.4B.5C.8D.10
例39.(2023·北京·高二北京铁路二中校考期中)直线分别与轴,轴交于两点,点在圆上,则面积的取值范围是( )
A.B.C.D.
例40.(2023·云南昆明·高三昆明一中校考阶段练习)已知圆,点为直线上的一个动点,是圆的两条切线,,是切点,当四边形(点为坐标原点)面积最小时,直线的方程为( )
A.B.
C.D.
考点7:直线与圆中的定点定值问题
例41.(2023·安徽合肥·高二合肥一中校联考期中)已知点,,动点满足,设动点的轨迹为曲线,过曲线与轴的负半轴的交点作两条直线分别交曲线于点(异于),且直线,的斜率之积为.
(1)求曲线的方程;
(2)证明:直线过定点.
例42.(2023·安徽合肥·高二合肥一中校联考期中)已知圆过,两点,且圆心在直线上.
(1)求圆的方程;
(2)设直线与圆交于A,两点,在直线上是否存在定点,使得直线,的倾斜角互补?若存在,求出点的坐标;若不存在,说明理由.
例43.(2023·北京·高二北京十五中校考期中)已知点,圆.
(1)求圆过点的切线方程;
(2)为圆与轴正半轴的交点,过点作直线与圆交于两点、,设、的斜率分别为、,求证:为定值.
例44.(2023·河南南阳·高二统考期中)已知圆.
(1)证明:圆过定点.
(2)当时,是否存在斜率为的直线交圆于、两点,使得以为直径的圆恰好经过原点?若存在,求出的方程;若不存在,说明理由.
例45.(2023·安徽马鞍山·高二统考期中)平面直角坐标系中,直线,圆:,圆与圆关于直线对称,是直线上的动点.
(1)求圆的标准方程;
(2)过点引圆的两条切线,切点分别为,设线段的中点是,是否存在定点,使得为定值,若存在,求出该定点的坐标;若不存在,请说明理由.
例46.(2023·河北唐山·高二校联考期中)已知圆,过圆上一点作直线分别与圆交于两点,设直线的斜率为.
(1)若圆的切线在轴和轴上的截距相等,求切线方程;
(2)若,求证:直线恒过定点.
例47.(2023·浙江宁波·高二校联考期中)已知圆O的方程为,与x轴的正半轴交于点N,过点作直线与圆O交于A、B两点.
(1)若坐标原点O到直线AB的距离为1,求直线AB的方程;
(2)如图所示,作一条斜率为-1的直线交圆于R,S两点,连接PS,PR,试问是否存在锐角,,使得为定值?若存在,求出该定值,若不存在,说明理由.
考点8:圆与圆的位置关系
例48.(2023·新疆伊犁·高二校联考期中)圆:与圆:的位置关系是( )
A.相交B.外离C.内含D.外切
例49.(2023·辽宁沈阳·高二校联考期中)“”是“圆与圆相切”的( )
A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件
例50.(2023·四川雅安·高二雅安中学校联考期中)已知圆,圆,则“”是“圆与圆外离”的( )
A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件
例51.(2023·浙江嘉兴·高二校考期中)已知圆:与圆:,则两圆的位置关系是( )
A.相离B.外切C.相交D.内切
例52.(2023·山东潍坊·高二统考期中)已知圆:,圆:,则与的位置关系是( )
A.外切B.内切C.外离D.相交
考点9:两圆的公共弦问题
例53.(2023·浙江·高二温州中学校联考期中)已知圆与圆相交于A,B两点,则=( )
A.B.C.D.
例54.(2023·天津·高二校考期中)圆与圆的公共弦所在直线恒过点( )
A.B.C.D.
例55.(2023·海南海口·高二海口一中校考期中)圆:与圆:相交于A,B两点,则等于( )
A.B.C.D.
例56.(2023·浙江台州·高二台州一中校考期中)圆:与圆:的公共弦所在直线方程为( )
A.B.
C.D.
例57.(2023·山西运城·高二校联考阶段练习)圆与圆相交于两点,则等于( )
A.B.C.D.
考点10:公切线问题
例58.(2023·黑龙江·高二统考期中)圆:和圆:的公切线的条数为( )
A.1B.2C.3D.4
例59.(2023·河北沧州·高二校联考期中)古希腊数学家阿波罗尼奥斯(约公元前262~公元前190年)的著作《圆锥曲线论》是古代数学的重要成果.其中有这样一个结论:平面内与两点距离的比为常数()的点的轨迹是圆,后人称这个圆为阿波罗尼斯圆.已知点,动点满足,则点P的轨迹与圆的公切线的条数为( )
A.1B.2C.3D.4
例60.(2023·广西玉林·高二统考期中)已知圆:,圆:,则下列说法正确的是( )
A.圆与圆公共弦所在直线的方程为
B.圆与圆有两条公切线
C.是圆与圆的一条公切线
D.圆与圆上均恰有两点到直线的距离为2
例61.(2023·全国·高二专题练习)已知圆,圆,则下列不是,两圆公切线的直线方程为( )
A.B.
C.D.
例62.(2023·山东聊城·高二统考期末)已知圆:与圆:相内切,则与的公切线方程为( )
A.B.
C.D.
考点11:圆系方程的应用
例63.过圆与的交点,且圆心在直线上的圆的方程是_______.
例64.已知圆与圆相交于A、B两点.
(1)求公共弦AB所在直线方程;
(2)求过两圆交点A、B,且过原点的圆的方程.
例65.已知圆.求证:对任意不等于的实数,方程是通过两个已知圆交点的圆的方程.
例66.已知圆和圆.
(1)求证:两圆相交;
(2)求过点,且过两圆交点的圆的方程.
(2023·北京通州·高二期中)经过点以及圆与圆交点的圆的方程为________.
【提升练习】
一、单选题
1.(2023·江苏盐城·高二盐城市第一中学校考期中)已知点P是直线上的动点,过点P引圆的两条切线PM,PN,M,N为切点,则PM的最小值为时,r的值为( )
A.1B.2C.D.
2.(2023·四川·高二校考期中)直线与曲线恰有两个交点,则实数的取值范围是( )
A.B.
C.D.或
3.(2023·四川达州·高二四川省万源中学校考期中)已知圆C: ,直线:,直线被圆C截得的弦长最短时,实数m的值为( )
A.B.C.1D.
4.(2023·北京通州·高二统考期中)过直线上一点作圆的两条切线,,切点分别为A,B,当直线,关于对称时,线段的长为( )
A.4B.C.D.2
5.(2023·江苏盐城·高二校考期中)已知,,动点满足,则点的轨迹与圆相交的弦长等于( )
A.B.C.D.
6.(2023·天津武清·高二统考期中)在平面直角坐标系xOy中,若圆 (r>0)上存在点P,且点P关于直线的对称点Q在圆 上,则r的取值范围是( )
A.(2,+∞)B.[2,+∞)C.(2,8)D.[2,8]
7.(2023·江苏南京·高二期中)已知圆和两点、,若圆上存在一点,使得,则实数的取值范围是( )
A.B.C.D.
二、多选题
8.(2023·广东佛山·高二佛山市南海区九江中学校考阶段练习)已知圆:,过直线:上一点作圆的两条切线,切点分别为,,则( )
A.若点,则直线的方程为
B.面积的最小值为
C.直线过定点
D.以线段为直径的圆可能不经过点
9.(2023·河北唐山·高二校联考期中)已知圆,直线,直线与圆交于两点,则( )
A.直线恒过定点
B.当时,最长
C.当时,弦最短
D.最短弦长
10.(2023·山西太原·高二山西大附中校考期中)圆:与圆:,则下列说法正确的是( )
A.两圆公共弦所在的直线方程为B.两圆的位置关系为外切
C.公共弦长为D.两圆有四条公切线
11.(2023·江苏徐州·高二统考期中)古希腊著名数学家阿波罗尼斯发现:平面内到两个定点的距离之比为定值的点的轨迹是圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系中,,点满足.设点的轨迹为,则( )
A.轨迹的方程为
B.在轴上存在异于的两点,使得
C.当三点不共线时,射线是的角平分线
D.在轨迹上存在点,使得
三、填空题
12.(2023·广东东莞·高二东莞一中校考期中)已知圆心为的圆与直线:相切于点,则圆的方程为 .
13.(2023·江西·高二校联考阶段练习)已知斜率为1的直线与圆交于,两点,为弦的中点,若的横坐标为,则的取值范围为 .
14.(2023·安徽黄山·高二校联考期中)已知P为圆上一点,则点到P点的距离的最大值为 .
15.(2023·河北张家口·高二校联考阶段练习)写出同时与圆和圆都相切的一条直线方程 .
四、解答题
16.(2023·福建福州·高二校联考期中)在平面直角坐标系中,已知圆的圆心在轴上,
(1)若圆过点、点, 求圆的方程;
(2)若圆与直线相切,且原点不在圆外,求当圆的面积最小时圆的方程.
17.(2023·北京·高二北京市第十二中学校考期中)已知点及圆.
(1)求圆心的坐标及半径的大小;
(2)设过点的直线与圆交于两点,当时,求以线段为直径的圆的方程;
(3)设直线与圆交于两点,是否存在实数,使得过点的直线垂直平分弦?若存在,求出实数的值;若不存在,请说明理由.
18.(2023·湖北武汉·高二湖北省武昌实验中学校联考期中)已知圆,圆:,圆:,这三个圆有一条公共弦.
(1)当圆的面积最小时,求圆的标准方程;
(2)在(1)的条件下,直线同时满足以下三个条件:
(i)与直线垂直;
(ii)与圆相切;
(iii)在轴上的截距大于0,
若直线与圆交于,两点,求.
19.(2023·四川达州·高二四川省万源中学校考期中)已知圆过点和点,并且圆心在直线上.点是直线上一动点,过点引圆的两条切线、,切点分别为,.
(1)求圆的标准方程;
(2)当四边形的面积最小时,求点的坐标及直线的方程.
20.(2023·吉林松原·高二前郭尔罗斯县第五中学校考期中)在平面直角坐标系中,已知两个定点,,动点P满足,设动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)过直线上一动点作曲线C的两条切线,切点为M,N,探究:直线MN是否过定点.
清单14 导数的综合问题-2023-2024学年高二数学上学期期末常考题型+易错题(苏教版): 这是一份清单14 导数的综合问题-2023-2024学年高二数学上学期期末常考题型+易错题(苏教版),文件包含清单14导数的综合问题9个考点梳理+题型解读+提升训练原卷版docx、清单14导数的综合问题9个考点梳理+题型解读+提升训练解析版docx等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。
清单11 数列的通项公式 -2023-2024学年高二数学上学期期末常考题型+易错题(苏教版): 这是一份清单11 数列的通项公式 -2023-2024学年高二数学上学期期末常考题型+易错题(苏教版),文件包含清单11数列的通项公式10个考点梳理+题型解读+提升训练原卷版docx、清单11数列的通项公式10个考点梳理+题型解读+提升训练解析版docx等2份试卷配套教学资源,其中试卷共61页, 欢迎下载使用。
清单09 玩转圆锥曲线经典题型-2023-2024学年高二数学上学期期末常考题型+易错题(苏教版): 这是一份清单09 玩转圆锥曲线经典题型-2023-2024学年高二数学上学期期末常考题型+易错题(苏教版),文件包含清单09玩转圆锥曲线经典题型12个考点梳理+题型解读+提升训练原卷版docx、清单09玩转圆锥曲线经典题型12个考点梳理+题型解读+提升训练解析版docx等2份试卷配套教学资源,其中试卷共108页, 欢迎下载使用。












