河南省周口市西华县2023-2024学年九年级上学期11月月考数学试题

这是一份河南省周口市西华县2023-2024学年九年级上学期11月月考数学试题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（考试时间：100分钟，满分：120分）
一、选择题（每小题3分，共30分）
下列各小题均有四个选项，其中只有一个是正确的．
1．下列说法不正确的是（ ）
A．的方程为一元二次方程 B．与关于原点对称
C．圆内接四边形的对角互补 D．过同一直线上的三个点不能作圆
2．如果从1，2，3，4中随机选取一个数，记为，再从这四个数中随机选取一个数，记为，则关于的一元二次方程没有实数根的概率为（ ）
A． B． C． D．
3．如图，在中，分别是上的动点，若点同时从两点出发分别沿方向向点匀速运动，它们的速度都是，则经过________秒后，的面积为面积的一半．（ ）
A．2 B．3 C．4 D．5
4．关于的一元二次方程的根的情况是（ ）
A．有两个不相等的实数根 B．有两个相等的实数根
C．没有实数根 D．不确定
5．若则平面直角坐标系内的点与点关于________对称．（ ）
A．轴 B．轴 C．原点 D．直线
6．把一元二次方程和的根写在四张背面无差别的卡片上（一张卡片上写一个根），将这些卡片背面朝上放在桌面上，小李从中随机抽取一张记下数字作为点的横坐标，放回重新洗匀后再随机抽出一张记下数字作为点的纵坐标，则点在以原点为圆心，5为半径的圆上的概率是（ ）
A． B． C． D．
7．已知为实数，且满足，则的值是（ ）
A．6 B．30 C．36 D．12
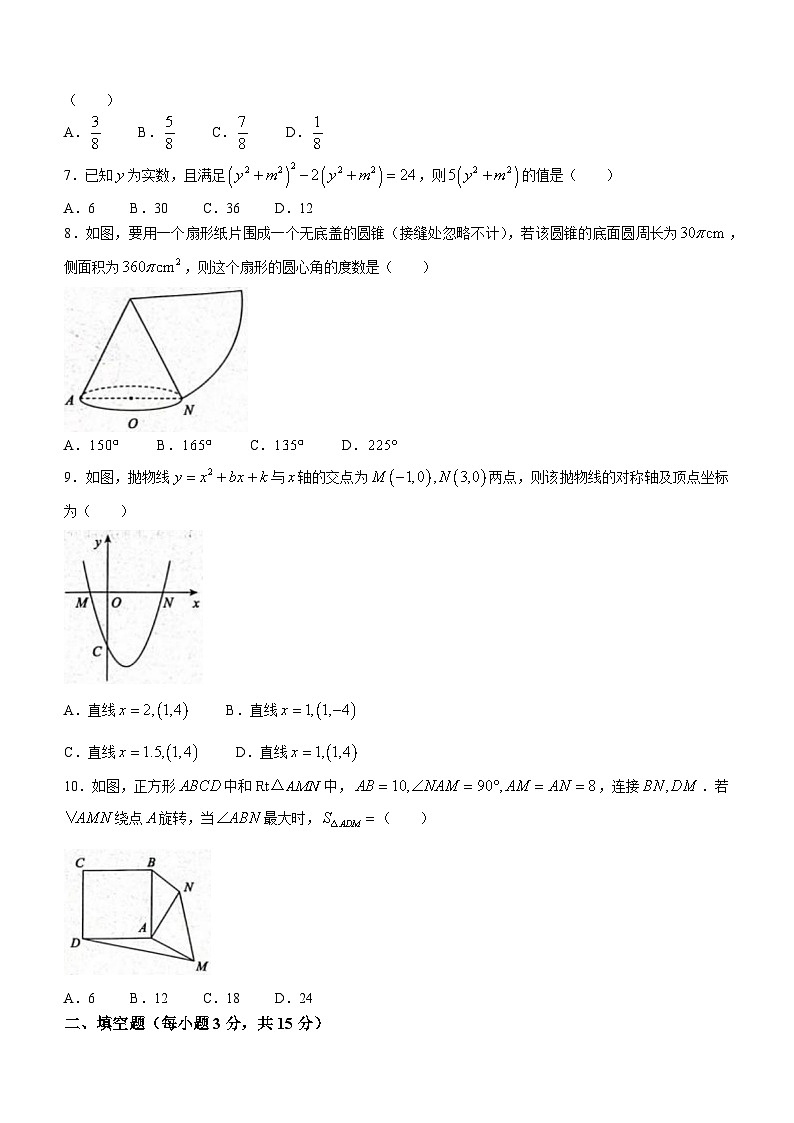
8．如图，要用一个扇形纸片围成一个无底盖的圆锥（接缝处忽略不计），若该圆锥的底面圆周长为，侧面积为，则这个扇形的圆心角的度数是（ ）
A． B． C． D．
9．如图，抛物线与轴的交点为两点，则该抛物线的对称轴及顶点坐标为（ ）
A．直线 B．直线
C．直线 D．直线
10．如图，正方形中和中，，连接．若绕点旋转，当最大时，（ ）
A．6 B．12 C．18 D．24
二、填空题（每小题3分，共15分）
11．下列图形中，左边的图形与右边的图形可看成中心对称的有________．
12．杂技表演时，微微从跷跷板右端处米）弹跳到人梯顶端椅子处，借助其弹性可以将演员弹跳到离地面最高点处，若其身体（看成一个点）的路线为抛物线的一部分，已知人梯高米，演员弹跳到最高点处后落到人梯顶端椅子处算表演成功，为了表演成功，人梯离起跳点的水平距离应为________米．
13．的边，边的长是一元二次方程的两根，则的外接圆的半径是________．
14．如图，在中，半径为5，是两条弦，于点于点．点在上运动，则的最小值为________．
15．如图，小明在玩游戏，脱手镖游戏板是由大小相等的小正方形格子构成，向游戏板随机投掷一枚脱手镖，击中空白区域的概率是________．
三、解答题（本大题共8个小题，共75分）
16．（10分）
解方程：（1） （2）
17．（9分）如图，在平面直角坐标系中，，，将向右平移4个单位长度，得到．
（1）画出关于轴对称的．
（2）将绕原点旋转，画出旋转后的．
（3）在中，（ ）与（ ）成中心对称，对称中心的坐标是（ ）
18．（9分）某社区居委会有M，N两个不透明的袋子，各装有三个小球，M袋中的三个小球上分别标记数字6，7，8；N袋中的三个小球分别标记数字7，8，9．这六个小球除标记的数字外，其余完全相同
（1）将M袋中的小球摇匀，从中随机摸出一个小球，则摸出的这个小球标记的数字是奇数的概率为（ ）；
（2）分别将M，N两个袋子中的小球摇匀，然后从M，N袋中各随机摸出一个小球，请利用画树状图或列表的方法，求摸出的这两个小球标记的数字之和为16的概率．
19．（9分）在中，，将一块等腰三角形的直角顶点放在斜边的中点处，将三角板绕点旋转，三角板的两直角边分别交射线于两点．旋转三角板得到的图形有三种情况，探究：
（1）三角板绕点旋转，观察线段与之间的数量关系？并结合第二个图说明理由．
（2）三角板绕点旋转，是否能成为等腰三角形？若能，指出所有的情况（即写出为等腰三角形时的长）；若不能，请说明理由．
20．（9分）在四边形中，，以点为圆心，长为半径作，连接，交于，
（1）试判断与的位畺关系，并说明理由．
（2）若，求图中阴影部分的面积．
21．（9分）如图，已知是的直径，为弦的中点．
（1）求证：；
（2）若，求阴影部分的面积．
22．（10分）某次商品交易会上，某商人成批购进纪念品的单价是22元，调查发现：销售单价是32元时，月销售量是230件，而销售单价每上涨1元，月销售量就减少10件，但每件纪念品售价不能高于40元．设每件纪念品的销售单价上涨了元时（为正整数），月销售利润为元．
（1）求与的函数关系式并直接写出自变量的取值范围．
（2）每件纪念品的售价定为多少元时，月销售利润恰为2520元？
（3）每件纪念品的售价定为多少元时可使月销售利润最大？最大利润是多少？
23．（10分）如图，已知一次函数的图象分别交轴轴于点，抛物线经过两点，在第一象限内的抛物线上有一动点，过作轴于，交于点．
（1）求此抛物线的解析式．
（2）设点的横坐标为，以为顶点的三角形面积为，求关于的函数关系式，并求出的最大值．
（3）若为线段的中点，为线段上一点，以为圆心，为半径作圆，当与轴相切时，求点的坐标．
参考答案
一、选择题
1-5 AAAAC 6-10 DBDD
10题解析：如图，作，交的延长线与
，当绕点旋转时，点在以为圆心，8为半径的圆上
当为此圆的切线时，即时，最大
此时，在中，
在和中
二、填空题
11．B，D 12．4 13．5 14． 15．
三、解答题
16．解：（1），，，或，
（2），，，，，
17．解：（1）如图所示
（2）如图所示
（3）
18．（1）
（2）画树状图如下，
共有9种等可能的结果，摸出的这两个小球标记的数字之和为16的结果有2种
摸出的这两个小球标记的数字之和为16的概率为
19．解：（1）．理由：是等腰直角三角形，是线段的中点
又∵，，
（2）能成为等腰三角形，共有以下三种情况：
①当时，此时点与点重合，
②当时，在线段上，在的延长线上，
③当时，
20．解：（1）与相切理由：过点作于点
，∴，∵，∴，∴
在和中，，
则点在上，是的半径．与相切
（2）是等边三角形，
，，，
在中，，解得
21．（1）证明：如图，连接是的直径，为弦的中点，，
；
（2）解：是的直径，为弦的中点，，
是的垂直平分线，，
是等边三角形，，
，，∴，
．
22．解：（1）由题意得
自变量的取值范围为，且为正整数．
（2）当时，解得（不合题意，舎去）．则（元）
答：每件纪念品的售价定为34元时，月销售利润为2520元．
（3）由题意得，，且m为正整数
当时，当时，
答：每件纪念品的售价定为38元或39元时，每个月可获得最大利润，最大月利润为2720元．
23．解：（1）在中，当时，；当时，，
把代入中，得解得
拋物线的解析式为
（2）如图，连接，∵点的坐标为
关于的函数关系式为，∵
当时，有最大值，为2
（3）设则
为线段的中点
以为半径的与轴相切
解得（舍去），点的坐标为．