2022-2023学年山西省临汾市七年级（上）期末数学试卷（含答案解析）

这是一份2022-2023学年山西省临汾市七年级（上）期末数学试卷（含答案解析），共16页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.−6的相反数是( )
A. −6B. −16C. 6D. 16
2.下列运算结果正确的是( )
A. 3a+2b=5abB. 2a3+3a2=5a5C. 3y3−2y3=1D. 3a2b−3ba2=0
3.某正方体的每个面上都有一个汉字，如图是它的一种表面展开图，那么在原正方体中，与“时”字所在面相对的面上的汉字是( )
A. 分
B. 垃
C. 圾
D. 类
4.根据国家统计局统计，2022年前三季度，夏粮早稻实现增产，全国夏粮早稻产量合计3511亿斤，秋粮生产总体稳定，从收获的情况看，全年粮食有望再获丰收．数据“3511亿”用科学记数法表示为( )
A. 3511×108B. 0.3511×1012C. 3.511×1011D. 35.11×1010
5.如图，能用∠1、∠ABC、∠B三种方法，表示同一个角的是( )
A. B.
C. D.
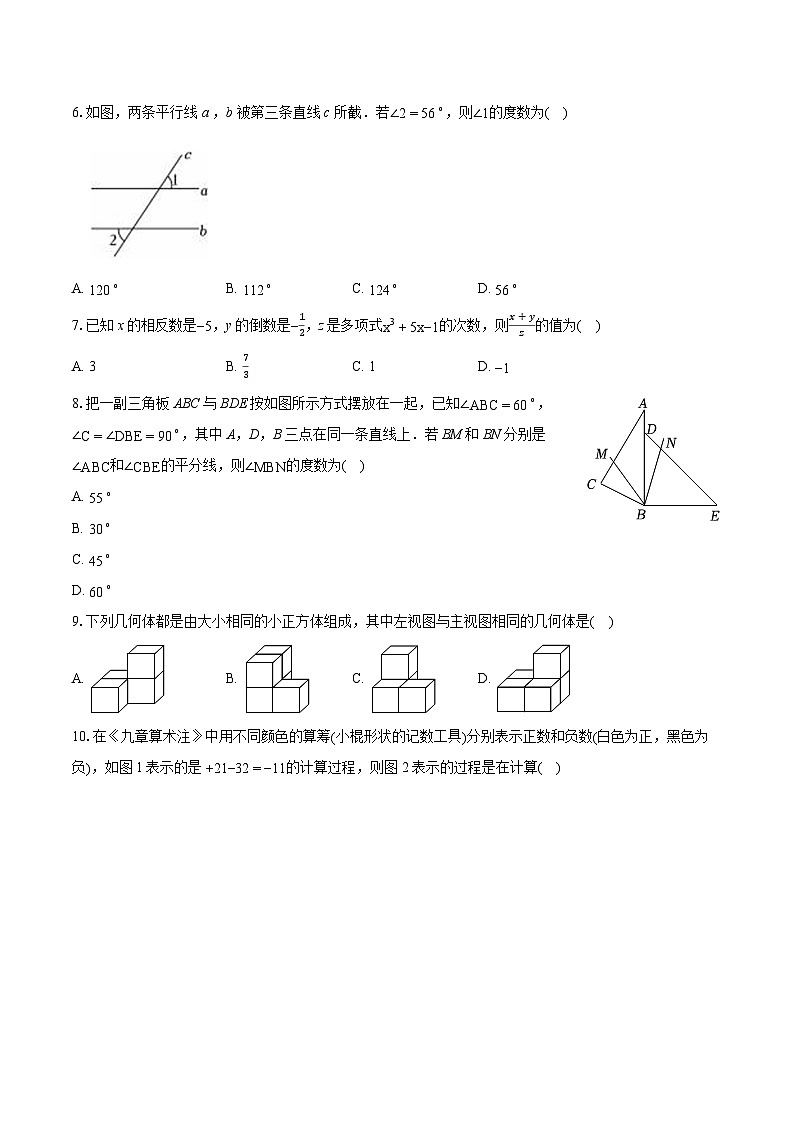
6.如图，两条平行线 a ，b 被第三条直线 c 所截．若∠2=56∘，则∠1的度数为( )
A. 120∘B. 112∘C. 124∘D. 56∘
7.已知x的相反数是−5，y的倒数是−12，z是多项式x3+5x−1的次数，则x+yz的值为( )
A. 3B. 73C. 1D. −1
8.把一副三角板ABC与BDE按如图所示方式摆放在一起，已知∠ABC=60∘，∠C=∠DBE=90∘，其中A，D，B三点在同一条直线上．若BM和BN分别是∠ABC和∠CBE的平分线，则∠MBN的度数为( )
A. 55∘
B. 30∘
C. 45∘
D. 60∘
9.下列几何体都是由大小相同的小正方体组成，其中左视图与主视图相同的几何体是( )
A. B. C. D.
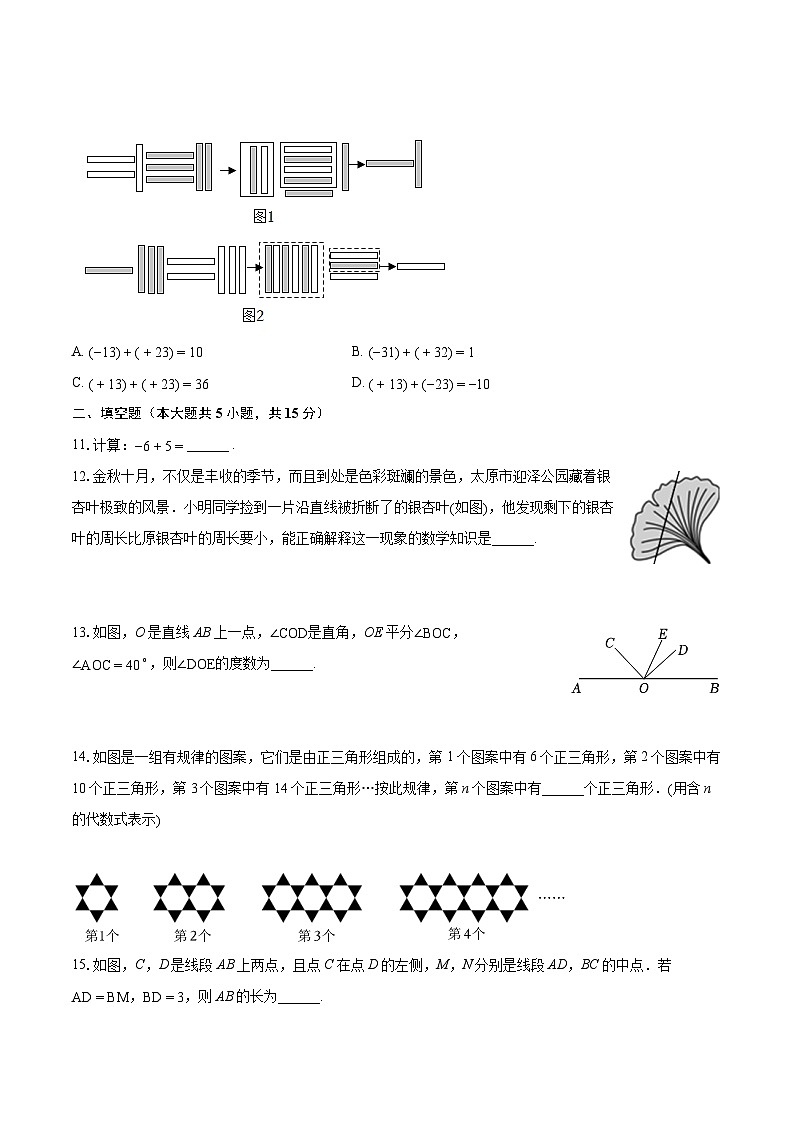
10.在《九章算术注》中用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(白色为正，黑色为负)，如图1表示的是+21−32=−11的计算过程，则图2表示的过程是在计算( )
A. (−13)+(+23)=10B. (−31)+(+32)=1
C. (+13)+(+23)=36D. (+13)+(−23)=−10
二、填空题（本大题共5小题，共15分）
11.计算：−6+5=______ .
12.金秋十月，不仅是丰收的季节，而且到处是色彩斑斓的景色，太原市迎泽公园藏着银杏叶极致的风景．小明同学捡到一片沿直线被折断了的银杏叶(如图)，他发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是______.
13.如图，O是直线AB上一点，∠COD是直角，OE平分∠BOC，∠AOC=40∘，则∠DOE的度数为______.
14.如图是一组有规律的图案，它们是由正三角形组成的，第1个图案中有6个正三角形，第2个图案中有10个正三角形，第3个图案中有14个正三角形…按此规律，第n个图案中有______个正三角形．(用含n的代数式表示)
15.如图，C，D是线段AB上两点，且点C在点D的左侧，M，N分别是线段AD，BC的中点．若AD=BM，BD=3，则AB的长为______.
三、解答题（本大题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤）
16.(本小题10分)
(1)计算：(−1)3−(1−12÷3)×|3−(−3)2|；
(2)先化简，再求值：−2y3+(3xy2−x2y)−2(xy2−y3)，其中x=−1，y=1.
17.(本小题7分)
如图，将方格纸中的图形先向右平行移动5格，再向下平行移动4格，画出平行移动后的图形．
18.(本小题8分)
阅读下面的解答过程，并填空．
如图，∠ABC=∠ACB，BD平分∠ABC，CE平分∠ACB，∠DBF=∠F.求证：CE//DF.
证明：∵BD平分∠ABC，CE平分∠ACB，(已知)
∴∠DBC=12∠______，∠ECB=12∠______.(角平分线的定义)
又∵∠ABC=∠ACB，(已知)
∴∠______=∠______.(等量代换)
又∵∠DBF=∠F，(已知)
∴∠______=∠______.(等量代换)
∴CE//DF.(______)
19.(本小题8分)
某原料仓库某一天的原料进出记录如下表(运进用正数表示，运出用负数表示)：
(1)这天仓库的原料比原来增加了还是减少了？请说明理由．
(2)根据实际情况，现有两种方案：
方案一：运进每吨原料费用6元，运出每吨原料费用9元；
方案二：不管运进还是运出费用都是每吨7元．
从节约运费的角度考虑，请说明选择哪种方案比较合适．
20.(本小题9分)
如图，点C在射线AB上，DF⊥AB于点F.
(1)使用圆规和直尺作图：(要求：保留作图痕迹，不写作法)
在射线AB上画出点E，使C为线段AE的中点，连接DE.
(2)连接CD，在线段CD，DE，DF中，线段______最短，依据是______.
(3)若∠ECD=62∘17′，求∠ACD的度数．
21.(本小题9分)
如图，长方形ABCD的长为m，宽为n，扇形ADE的半径为n，BF的长为12n.
(1)求图中阴影部分的面积S.(用含m，n的代数式表示)
(2)当m=8，n=4时，求S的值．(结果保留π)
22.(本小题11分)
阅读材料：
定义：数轴上的三点，如果其中一个点与近点距离是它与远点距离的12，则称该点是其他两个点的“倍分点”．例如数轴上点A，B，C所表示的数分别为−1，0，2，且满足AB=12BC，则点B是点A，C的“倍分点”．已知点A，B，C，M，N在数轴上所表示的数如图所示．
基础巩固：
(1)在A，B，C三点中，点______是点M，N的“倍分点”．
尝试应用：
(2)若数轴上点M是点A，D的“倍分点”，则点D在数轴上对应的数有______个．
灵活运用：
(3)若数轴上点N是点P，M的“倍分点”，且点P在点N的右侧，求此时点P在数轴上表示的数．
23.(本小题13分)
综合与实践
问题情境：
数学活动课上，老师展示了一个问题：如图1，直线l1//l2，直线l3与l1，l2分别交于点C，D，点A在直线l1上，且在点C的左侧，点B在直线l2上，且在点D的左侧，点P是直线l3上的一个动点(点P不与点C，D重合).当点P在点C，D之间运动时，试猜想∠PAC，∠APB，∠PBD之间的数量关系，并说明理由．
独立思考：
(1)请解答老师提出的问题．实践探究：
勤学小组对此问题进行了更深一步的思考：当点P在C，D两点的外侧运动时，∠PAC，∠APB，∠PBD之间的数量关系又是如何？
(2)如图2，当点P运动到点C上方时，试猜想∠PAC，∠APB，∠PBD之间的数量关系，并说明理由．
(3)如图3，当点P运动到点D下方时，请直接写出∠PAC，∠APB，∠PBD之间的数量关系．
答案和解析
1.【答案】C
【解析】解：−6的相反数是6，
故选：C.
利用相反数的定义判断即可．
本题考查了相反数，解题的关键是掌握相反数的定义．
2.【答案】D
【解析】解：A.3a+2b不是同类项，不能合并，选项A不符合题意；
B.2a3+3a2不是同类项，不能合并，选项B不符合题意；
C.3y3−2y3=y3，选项C不符合题意；
D.3a2b−3ba2=0，选项D符合题意；
故选：D.
根据合并同类项法则：合并同类项后，所得项的系数是合并前各同类项的系数之和，且字母连同它的指数不变即可求解．
本题主要考查了合并同类项，掌握合并同类项法则是解题的关键．
3.【答案】A
【解析】解：对于正方体的平面展开图中相对的面一定相隔一个小正方形，由图形可知，与“时”字所在面相对的面上的汉字是“分”．
故选：A.
利用正方体及其表面展开图的特点解题．
本题考查了正方体相对的两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．
4.【答案】C
【解析】解：3511亿=351100000000=3.511×1011.
故选：C.
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值<1时，n是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．
5.【答案】B
【解析】【分析】
本题考查了角的概念，角的表示方法有三种：
(1)用三个大写字母表示，顶点字母写在中间，每边上的点写在两旁；
(2)用一个顶点字母表示，注意角的顶点处必须只有一个角；
(3)靠近顶点处加上弧线，注上数字或希腊字母表示．
当角的顶点处只有一个角时，可以用一个大写字母表示这个角，也可以用三个大写字母表示这个角．
【解答】
解：A、顶点B处有四个角，不能用∠B表示，错误；
B、顶点B处有一个角，能同时用∠ABC，∠B，∠1表示，正确；
C、顶点B处有四个角，不能用∠B表示，错误；
D、顶点B处有三个角，不能用∠B表示，错误．
故选：B.
6.【答案】D
【解析】解：如图，
∵∠3和∠2是对顶角，
∴∠3=∠2=56∘，
∵a//b，
∴∠1=∠3=56∘.
故选：D.
由对顶角的性质得到∠3=∠2=56∘，根据平行线的性质得到∠1=∠3=56∘.
本题考查了直线平行的性质和对顶角的性质，掌握“两直线平行同位角相等”是解决问题的关键．
7.【答案】C
【解析】解：x的相反数是−5，则x=5，
而y的倒数是−12，则y=−2，
而z是多项式x3+5x−1的次数，则z=3，
则x+yz=5−23=1，
故选：C.
先根据相反数，倒数和多项式的定义分别求出x，y，z的值，再将x，y，z的值代入中即可求解．
本题主要考查了相反数，倒数和多项式，掌握相关的定义是解题的关键．
8.【答案】C
【解析】解：∵BM为∠ABC的平分线，
∴∠CBM=12∠ABC=12×60∘=30∘，
∵BN为∠CBE的平分线，
∴∠CBN=12∠EBC=12×(60∘+90∘)=75∘，
∴∠MBN=∠CBN−∠CBM=75∘−30∘=45∘.
故选：C.
由角平分线的定义可知∠CBM=12∠ABC=12×60∘=30∘，∠CBN=12∠EBC=12×(60∘+90∘)=75∘，再利用角的和差关系计算可得结果．
本题主要考查了角平分线的定义，利用角平分线的定义计算角的度数是解答此题的关键．
9.【答案】C
【解析】解：通过观察C选项的主视图和左视图均为：
故选：C.
通过观察四个选项中组合体的左视图和主视图，找到两个视图相同的几何体即可解答．
本题主要考查了简单组合体的三视图，解题关键在于掌握主视图和左视图的看法．
10.【答案】A
【解析】解：根据题意可知一横表示10，一竖表示1，
所以图2表示：(−13)+(+23)=10.
故选：A.
依据题意写出算式即可．
本题主要考查了有理数的加减运算和传统文化，本题是阅读型题目，理解图中的含义并熟练应用是解题关键．
11.【答案】−1
【解析】解：原式=−(6−5)=−1.
故答案为：−1
原式利用异号两数相加的法则计算即可得到结果．
此题考查了有理数的加法，熟练掌握加法法则是解本题的关键．
12.【答案】两点之间线段最短
【解析】解：由线段的性质可知，银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是两点之间线段最短，
故答案为：两点之间线段最短．
根据“两点之间线段最短”进行判断即可．
本题考查两点之间的距离，理解两点之间线段最短是正确解答的前提．
13.【答案】20∘
【解析】解：∵∠AOC=40∘，
∴∠BOC=180∘−∠AOC=180∘−40∘=140∘，
∵OE平分∠BOC，
∴∠COE=12∠BOC=70∘，
∵∠COD=90∘，
∴∠DOE=∠COD−∠COE=90∘−70∘=20∘，
故答案为：20∘.
由∠AOC的度数可以求得∠BOC的度数，由OE平分∠BOC，可以求得∠COE的度数，又由∠DOC=90∘可以求得∠DOE的度数．
本题考查了角平分线的定义，关键在于学生认真观察图形求得∠DOE的度数．
14.【答案】(4n+2)
【解析】解：第1个图案有6个三角形，即6=4×1+2；
第2个图案有10个三角形，即10=4×2+2；
第3个图案有14个三角形，即14=4×3+2；
…
按此规律摆下去，
第n个图案有(4n+2)个三角形．
故答案为：(4n+2).
根据图形的变化发现规律，即可用含n的代数式表示．
本题考查了规律型-图形的变化类、列代数式，解决本题的关键是根据图形的变化寻找规律．
15.【答案】9
【解析】解：∵AD=BM，
∴AD−MD=BM−MD，
∴AM=BD，
∵BD=3，
∴AM=3，
∵M是线段AD的中点，
∴AD=2AM=6，
∴AB=AD+BD=6+3=9.
故答案为：9.
根据AD=BM，得AM=BD=3，再根据M是线段AD的中点，得AD=2AM=6，所以AB=AD+BD=6+3=9.
本题考查了两点间的距离的求法，解题时利用了线段的和差，线段中点的性质，解决此类问题的关键是找出各个线段间的关系．
16.【答案】解：(1)原式=−1−(1−16)×|3−9|
=−1−56×6
=−1−5
=−6.
(2)原式=−2y3+3xy2−x2y−2xy2+2y3
=−2y3+2y3+3xy2−2xy2−x2y
=xy2−x2y，
当x=−1，y=1时，
原式=(−1)×12−(−1)2×1
=−2.
【解析】(1)根据有理数的乘方运算、有理数的加减运算以及乘除运算法则即可求出答案．
(2)根据整式的加减运算法则进行化简，然后将x与y的值代入原式即可求出答案．
本题考查有理数的乘方运算、有理数的加减运算以及乘除运算法则，整式的加减运算法则进行化简，本题属于基础题型．
17.【答案】解：如图即为所求：

【解析】根据平移规律找到平移后的关键点，画出即可．
本题考查了平移变换，掌握平移的性质是解题的关键．
18.【答案】ABC ACB DBC ECB ECB F 同位角相等，两直线平行
【解析】证明：∵BD平分∠ABC，CE平分∠ACB，(已知)
∴∠DBC=12∠ABC，∠ECB=12∠ACB.(角平分线的定义)
又∵∠ABC=∠ACB，(已知)
∴∠DBC=∠ECB.(等量代换)
又∵∠DBF=∠F，(已知)
∴∠ECB=∠F.(等量代换)
∴CE//DF.(同位角相等，两直线平行)
故答案为：ABC；ACB；DBC；ECB；ECB；F；同位角相等，两直线平行．
根据题意和图形，可以在证明过程中写入相应的条件，本题得以解决．
本题考查平行线的判定，解答本题的关键是明确题意，利用数形结合的思想解答．
19.【答案】解：(1)减少了，
理由：(−2)×2+3×1+(−1)×3+2×4+(−4)×2=−4(吨)；
(2)运进数量：3×1+2×4=3+8=11(吨)，
运出数量：|−2|×2+|−1|×3+|−4|×2=15(吨)，
方案一：11×6+15×9=201(元)，
方案二：(11+15)×7=182(元)，
∵201>182，
∴选择方案二比较合适．
【解析】(1)求出这几次进出数量的和，根据“和”的符号得出答案；
(2)求出两种方案的费用即可．
本题考查正数和负数，理解正数和负数的意义是解题的关键．
20.【答案】DF 垂线段最短
【解析】解：(1)如图：
点E即为所求；
(2)在线段CD，DE，DF中，线段DF最短，根据是垂线段最短，
故答案为：DF，垂线段最短；
(3)∵∠ECD+∠ACD=180∘，∠ECD=62∘17′，
∴∠ACD=180∘−∠ECD=180∘−62∘17′=117∘43′.
(1)以C为圆心，AC长为半径作弧交AB于E，则E即为所求；
(2)由垂线段最短可得答案；
(3)由邻补角可得答案．
本题考查作图-复杂作图，解题的关键是掌握中点，垂线段等概念．
21.【答案】解：(1)由图可得，
阴影部分的面积S=mn+14πn2−12(m+n)×12n=mn+14πn2−14mn−14n2=34mn+π−14n2，
即阴影部分的面积S是34mn+π−14n2；
(2)当m=8，n=4时，
S=34×8×4+π−14×42=20+4π，
即当m=8，n=4时，S的值是20+4π.
【解析】(1)根据图形可知，阴影部分的面积S=长方形的面积+扇形的面积-三角形的面积，然后代入字母计算即可；
(2)将m=8，n=4代入(1)中的S，计算即可解答本题．
本题考查扇形面积，列代数式、代数式求值，解答本题的关键是明确题意，列出相应的代数式，求出相应式子的值．
22.【答案】B 4
【解析】解：(1)∵BM=0−(−3)=3，BN=6−0=6，
∴BM=12BN，
∴点B是点M，N的“倍分点”，
故答案为：B；
(2)AM=−1−(−3)=2，设D点坐标为x，
①当DM=12AM时，DM=1，
∴|x−(−3)|=1，
解得：x=−2或−4，
②当AM=12DM时，DM=2AM=4，
∴|x−(−3)|=4，
解得：x=1或−7，
综上所述，则点D对应的数有4个，分别是−2，−4，1，−7，
故答案为：4；
(3)MN=6−(−3)=9，
当PN=12MN时，PN=12×9=92，
∵点P在点N的右侧，
∴此时点P表示的数为212，
当MN=12PN时，PN=2MN=2×9=18，
∵点P在点N的右侧，
∴此时点P表示的数为24，
综上所述，点P表示的数为212或24.
(1)利用“倍分点”的定义即可求得答案；
(2)设D点坐标为x，利用“倍分点”的定义，分两种情况讨论即可求出答案；
(3)利用“倍分点”的定义，结合点P在点N的右侧，分两种情况讨论即可求出答案．
本题考查了数轴结合新定义“倍分点”，正确理解“倍分点”的含义是解决问题的关键．
23.【答案】解：(1)∠APB=∠PAC+∠PBD.
理由如下：如图1，过点P作PE//l1，则∠APE=∠PAC.
∵l1//l2，
∴EP//l2，
∴∠BPE=∠PBD，
∴∠APB=∠APE+∠BPE=∠PAC+∠PBD；
(2)∠APB=∠PBD−∠PAC.
理由如下：如图2，过点P作FP//l1，则∠APF=∠PAC.
∵l1//l2，
∴FP//l2，
∴∠BPF=∠PBD，
∴∠APB=∠BPF−∠APF=∠PBD−∠PAC；
(3)∠APB=∠PAC−∠PBD.
理由如下：如图3，过点P作MP//l1，则∠APM=∠PAC.
∵l1//l2，
∴MP//l2，
∴∠BPM=∠PBD，
∴∠APB=∠APM−∠BPM=∠PAC−∠PBD.
【解析】(1)过P点作EP//l1，利用两直线平行内错角相等得到一对角相等，再由与平行线中的一条平行，与另一条也平行得到EP//l2，利用两直线平行内错角相等得到一对角相等，等量代换即可得证；
(2)∠APB=∠PBD−∠PAC，如图2所示，过点P作FP//l1，同理即可得证；
(3)∠APB=∠PAC−∠PBD，如图2所示，过点P作MP//l1，同理即可得证．
此题考查了平行线的性质，熟练掌握平行线的判定定理与性质定理是解本题的关键．进出数量(单位：吨)
−2
3
−1
2
−4
进出次数
2
1
3
4
2