青海省西宁市大通县2024届高三上学期开学摸底考试数学（理）试卷(含答案)

这是一份青海省西宁市大通县2024届高三上学期开学摸底考试数学（理）试卷(含答案)，文件包含专题一近代中国人民的反侵略斗争同步练习教师版2023-2024部编版历史八年级上册docx、专题一近代中国人民的反侵略斗争同步练习学生版2023-2024部编版历史八年级上册docx等2份试卷配套教学资源，其中试卷共19页， 欢迎下载使用。


一、选择题
1、已知集合,则( )
A.B.C.D.
2、已知复数z满足,则在复平面内复数z对应的点位于( )
A.第一象限B.第二象限C.第三象限D.第四象限
3、已知x,y满足约束条件则目标函数的最大值为( )
A.B.C.4D.5
4、随机变量X服从正态分布,若,则( )
5、已知为第四象限角,且,则( )
A.B.C.D.
6、已知,是两个不重合的平面,且直线,则“”是“”的()
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
7、北京地处中国北部、华北平原北部,东与天津毗连,其余方向均与河北相邻,是世界著名古都,也是国务院批复确定的中国政治中心、文化中心、国际交往中心、科技创新中心.为了感受这座古今中外闻名的城市,某学生决定在高考后游览北京,计划6天游览故宫、八达岭长城、虍和园、“水立方”、“鸟巢”、798艺术区、首都博物馆7个景点,如果每天至少游览一个景点,且“水立方”和“鸟巢”在同一天游览,故宫和八达岭长城不在相邻两天游览,那么不同的游览顺序共有( )
A.120种B.240种C.480种D.960种
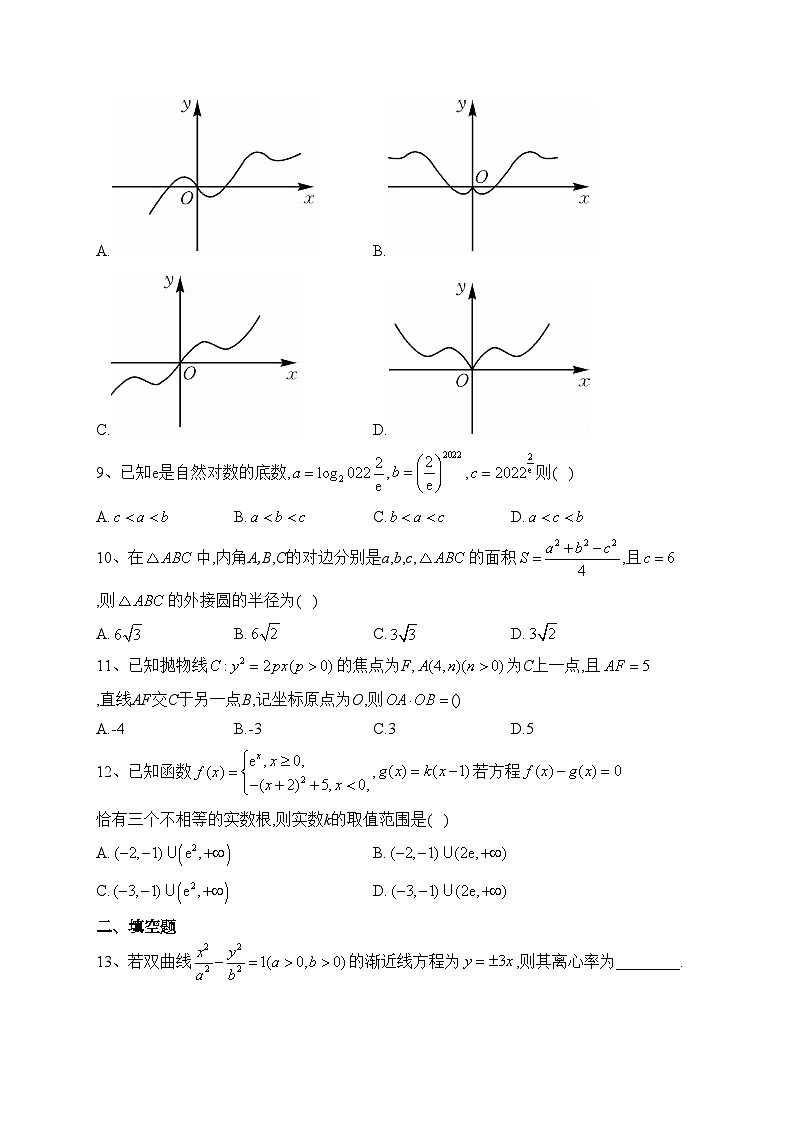
8、函数的图象有可能是( )
A.B.
C.D.
9、已知e是自然对数的底数,,,则( )
A.B.C.D.
10、在中,内角A,B,C的对边分别是a,b,c,的面积,且,则的外接圆的半径为( )
A.B.C.D.
11、已知抛物线的焦点为F,为C上一点,且,直线AF交C于另一点B,记坐标原点为O,则()
A.-4B.-3C.3D.5
12、已知函数,若方程恰有三个不相等的实数根,则实数k的取值范围是( )
A.B.
C.D.
二、填空题
13、若双曲线的渐近线方程为,则其离心率为________.
14、在中,点D是边AC上的一点,,点P满足,若,则__________.
15、已知球O的表面积为,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,该四棱锥的高为_________.
16、已知函数的部分图象如图所示,且阴影部分的面积为,若函数在区间上单调递增,则实数m的取值范围是____________.
三、解答题
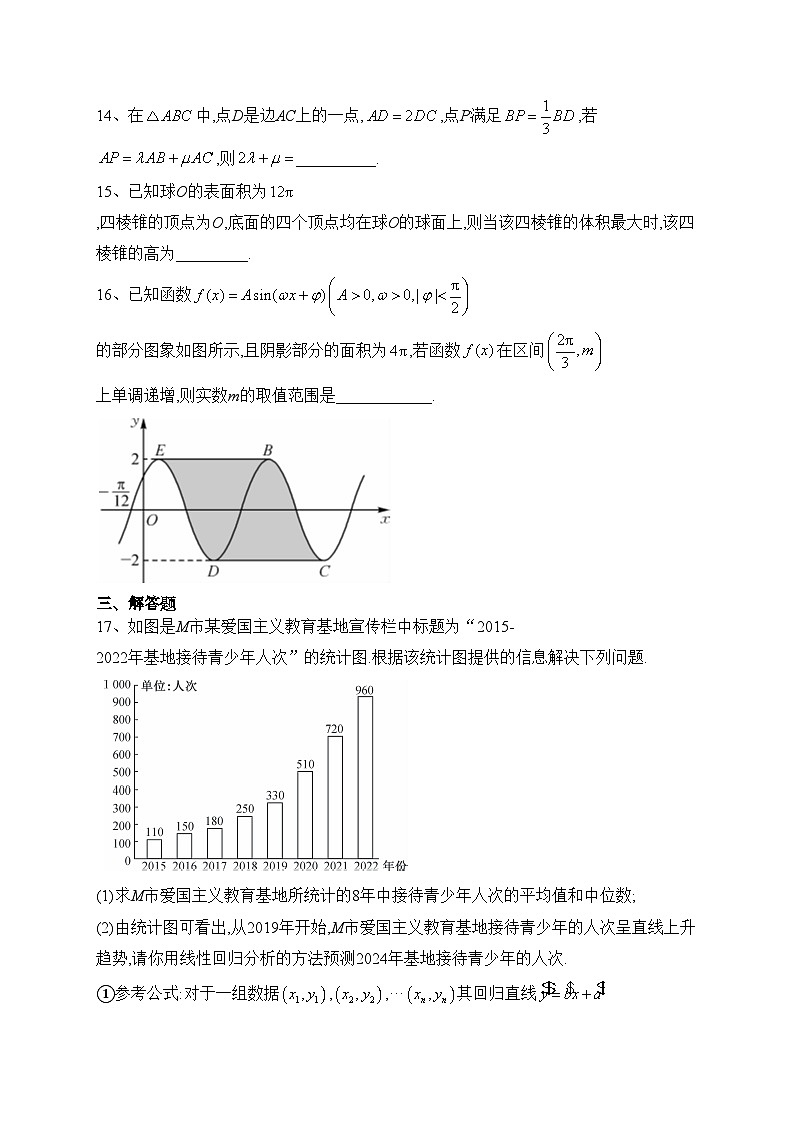
17、如图是M市某爱国主义教育基地宣传栏中标题为“2015-2022年基地接待青少年人次”的统计图.根据该统计图提供的信息解决下列问题.
(1)求M市爱国主义教育基地所统计的8年中接待青少年人次的平均值和中位数;
(2)由统计图可看出,从2019年开始,M市爱国主义教育基地接待青少年的人次呈直线上升趋势,请你用线性回归分析的方法预测2024年基地接待青少年的人次.
①参考公式:对于一组数据,,···其回归直线的斜率和截距的最小二乘法公式分别为,.
②参考数据:
18、在等比数列中,,,分别是下表第一,第二,第三列中的某一个数,且,,中的任何两个数不在下表的同一行.
(1)写出,,并求数列的通项公式;
(2)若数列满足,求数列的前n项和.
19、如图,在四棱锥中,平面ABCD,,,,,E是棱PB上一点.
(1)求证:平面平面PBC;
(2)若E是PB的中点,求直线PA与平面EAC所成角的正弦值.
20、已知椭圆E的中心为坐标原点,对称轴为x轴、y轴,且过,两点.
(1)求E的方程;
(2)若,过的直线l与E交于M,N两点,求证:.
21、已知函数.
(1)若,求的极值;
(2)若有且仅有两个零点,求a的取值范围.
22、在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,曲线,的极坐标方程分别为,.
(1)求曲线,的直角坐标方程;
(2)若曲线与x轴交于点P,曲线和曲线的交点为A,B,求的值.
23、已知函数.
(1)解不等式;
(2)若的最小值为m,且,求的最小值.
参考答案
1、答案：B
解析：因为,所以,又,所以,故选B.
2、答案：A
解析：因为,所以,在复平面内复数z对应的点为,位于第一象限.故选A.
3、答案：C
解析：画出满足约束条件的平面区域,如图所示,平移直线,当经过直线与的交点时,目标函数z取得最大值,即.故选C.
4、答案：A
解析：因为随机变量X服从正态分布,所以.故选A.
5、答案：C
解析：因为,所以,因为为第四象限角,
所以,所以,
所以.
故选C.
6、答案：B
解析：若,则,或,故充分性不成立;因为,是两个不重合的平面,直线,若,则存在直线,满足,因为,所以,所以,故必要性成立.所以“”是“”的必要不充分条件.故选B.
7、答案：D
解析：分2步进行分析:①将“水立方”和“鸟巢”看成一个整体,与颐和园、798艺术区、首都博物馆全排列,有种情况,②排好后,有5个空位可用,在其中任选2个,安排故宫和八达岭长城,有种情况,则有种不同的游览顺序.
故选D.
8、答案：A
解析：函数的定义域为R,,可得为奇函数,其图象关于原点对称,可排除选项B、D;的导数为,当时,,单调递减;当时,,单调递增,则在处取得极小值,可排除选项C.故选A.
9、答案：B
解析：因为,,所以,,所以.故选B.
10、答案：D
解析：因为,所以,
所以,又,所以.
设的外接圆的半径为r,所以,解得.
故选D.
11、答案：B
解析：由题意得,抛物线的准线为,
因为为C上一点,且,所以,,
解得,故抛物线,焦点为,
所以AF的方程为,代入,得,
整理得,解得或,因为B为C上一点,则,
所以,所以,所以.
故选B.
12、答案：A
解析：
13、答案：
解析：双曲线的渐近线方程为,即,,离心率.
14、答案：
解析：因为点D是边AC上的一点,,
所以,
所以
.
又,所以,所以.
15、答案：1
解析：设球O的半径为R,所以,解得.
设该四棱锥底面为四边形ABCD,四边形ABCD所在小圆半径为r、
设四边形ABCD对角线夹角为,
则,
当且仅当四边形ABCD为正方形时等号成立.即当四棱雉的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积的最大值为.设四棱锥的高为,
所以.则.令,所以,所以当时,,当时,,所以在上单调递增,在上单调递减,所以,所以当该四棱锥的体积最大时,该四棱雉的高为1.
16、答案：
解析：
17、答案：(1)平均数为:401.25
中位数为:290
(2)1365
解析:(1)平均数为:
,
中位数为:.
(2),,
则,
所以线性回归方程,
所以在2024年时,
所以,
预测2024年基地接待青少年的人次为.
18、答案：(1)
(2)
解析：(1)根据等比数列的定义和表格中数据,
得到,,
即数列是首项为2,公比为-2的等比数列,
故.
(2)因为,
所以
.
19、答案：(1)见解析
(2)
解析：(1)证明:因为平面ABCD,平面ABCD,
所以.设AB的中点为G,连接CG,如图所示.
因为G是AB的中点,所以,又,
所以,所以四边形ADCG为平行四边形,
所以,又,所以.
在中,,,
所以.在中,,,
所以.在中,,,
所以,所以.又,BC,平面PBC,
所以平面PBC又平面EAC,所以平面平面PBC.
(2)以C为坐标原点,分别以直线CG、CD、CP为x轴、y轴、z轴建立如图所示的空间直角坐标系,
所以,,,
所以,,,
设平面EAC的一个法向量,
所以
令,解得,
所以平面EAC的一个法向量,
设直线PA与平面EAC所成的角为,
则,
即直线PA与平面EAC所成角的正弦值为.
20、答案：(1)
(2)见解析
解析：(1)设E的方程为,
过,
所以
解得,
所以E的方程为.
(2)证明:当直线l的斜率为0时,直线l的方程为,
所以,或,.
所以.
当直线l的斜率不为0时,设直线l的方程为,,,
由得,
所以,
,
所以,
所以
所以QP平分,所以.
21、答案：(1)见解析
(2)
解析：(1)若,所以,
令,则在上恒成立,
所以在上单调递增,即在上单调递增,
又,所以当时,,当时,
,所以在上单调递减,在上单调递增.
又,所以的极小值为0,无极大值.
(2)若有且仅有两个零点,即在内有两个不等实根,
令,
则,
当时,在上恒成立,所以在上单调递增,
所以在上至多有1个零点,不符合题意;
当时,令,解得,令,解得,所以在上单调递减,在上单调递增,所以.
若,则,所以在上无零点,不符合题意;
若,则,所以在上有且仅有一个零点,不符合题意;
若,则,
又,,在上单调递增,
所以在上有且仅有一个零点;
令,所以,令,解得,令,解得,所以在上单调递减,在上单调递增,所以,即,所以,
又,在上单调递减,
所以在上有且仅有一个零点.所以在上有且仅有两个零点.
综上,a的取值范围是.
22、答案：(1)
(2)10
解析：(1)因为曲线的极坐标方程为,
又,所以,
所以曲线的直角坐标方程为.
因为曲线的极坐标方程为,
所以,
所以曲线的直角坐标方程为.
(2)由题意知,故直线的一个参数方程为(t为参数).
把的参数方程代入,得,
所以,设A,B所对应的参数分别为,
则,所以,同号,
所以.
23、答案：(1)
(2)2
解析:(1)
不等式等价于或或
解得,
故不等式的解集为.
(2)因为,当且仅当时等号成立,所以,
所以,
所以.
因为,当且仅当等号成立,所以,
当且仅当时等号成立,故的最小值为2.
0
1
2
3
-300
-120
90
330
第一列
第二列
第三列
第一行
-1
-4
16
第二行
2
-6
-10
第三行
5
12
8