数学高考第一轮复习特训卷（文科）9 导数与函数的单调性、极值、最值

点点练9  导数与函数的单调性、极值、最值

一      基础小题练透篇

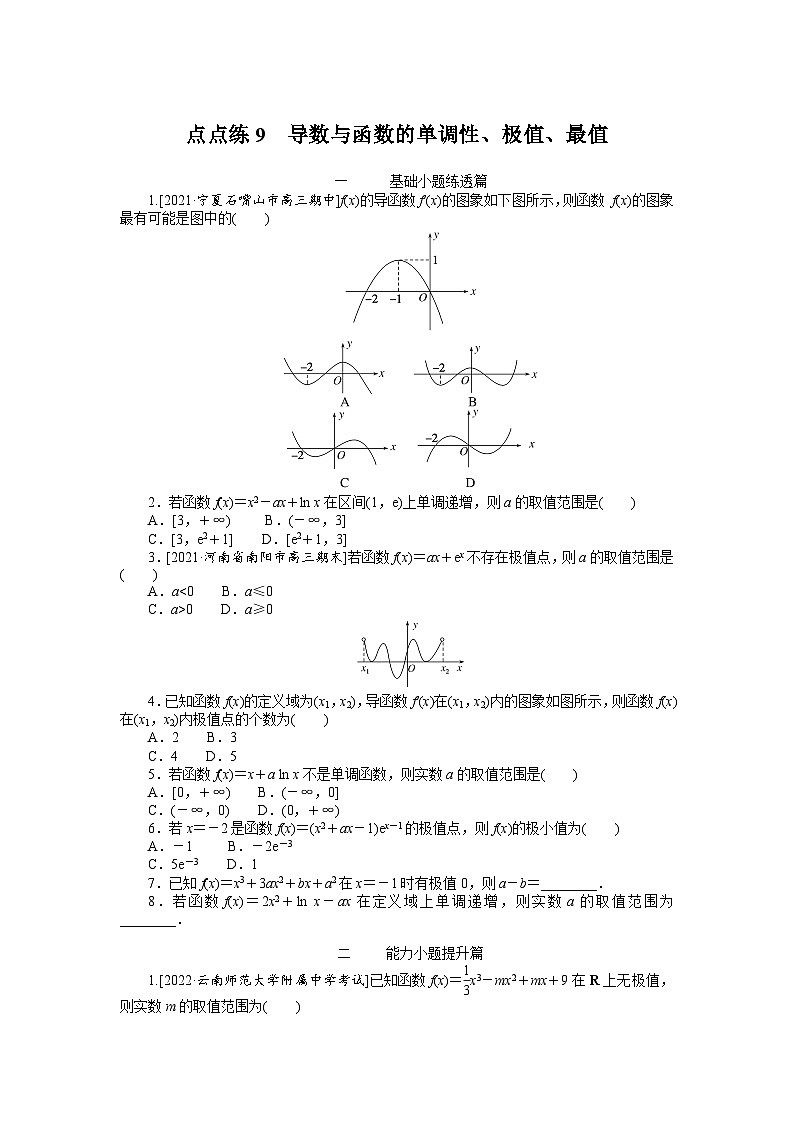
1.[2021·宁夏石嘴山市高三期中]f(x)的导函数f′(x)的图象如下图所示，则函数 f(x)的图象最有可能是图中的(　　)

2．若函数f(x)＝x2－ax＋ln x在区间(1，e)上单调递增，则a的取值范围是(　　)

A．[3，＋∞)     B．(－∞，3]

C．[3，e2＋1]    D．[e2＋1，3]

3．[2021·河南省南阳市高三期末]若函数f(x)＝ax＋ex不存在极值点，则a的取值范围是(　　)

A．a<0    B．a≤0

C．a>0    D．a≥0

4．已知函数f(x)的定义域为(x1，x2)，导函数f′(x)在(x1，x2)内的图象如图所示，则函数f(x)在(x1，x2)内极值点的个数为(　　)

A．2    B．3

C．4    D．5

5．若函数f(x)＝x＋a ln x不是单调函数，则实数a的取值范围是(　　)

A．[0，＋∞)    B．(－∞，0]

C．(－∞，0)    D．(0，＋∞)

6．若x＝－2是函数f(x)＝(x2＋ax－1)ex－1的极值点，则f(x)的极小值为(　　)

A．－1     B．－2e－3

C．5e－3    D．1

7．已知f(x)＝x3＋3ax2＋bx＋a2在x＝－1时有极值0，则a－b＝________．

8．若函数f(x)＝2x2＋ln x－ax在定义域上单调递增，则实数a的取值范围为________．

二     能力小题提升篇

1.[2022·云南师范大学附属中学考试]已知函数f(x)＝x3－mx2＋mx＋9在R上无极值，则实数m的取值范围为(　　)

A．(－∞，0)∪(1，＋∞)

B．(－∞，0]∪[1，＋∞)

C．(0，1)

D．[0，1]

2．[2022·安徽省阜阳市期末]若函数f(x)＝x3－ax2(a>0)的极大值点为a－2，则a＝(　　)

A．1    B．2    C．4    D．6

3．[2022·河南省高三模拟]函数f(x)＝x ln x－x在上的最小值为(　　)

A．－    B．－1

C．0            D．2ln 2－2

4．[2021·河北省沧州市三模]已知函数f(x)＝－x，则(　　)

A．f(x)的单调递减区间为(0，1)

B．f(x)的极小值点为1

C．f(x)的极大值为－1

D．f(x)的最小值为－1

三      高考小题重现篇

1.[浙江卷]函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则函数y＝f(x)的图象可能是(　　)

2．[江苏卷]若函数f(x)＝2x3－ax2＋1(a∈R)在(0，＋∞)内有且只有一个零点，则f(x)在[－1，1]上的最大值与最小值的和为________.

3．[全国卷Ⅰ]已知函数f(x)＝2sin x＋sin 2x，则f(x)的最小值是________.

4．[山东卷]若函数exf(x)(e＝2.718 28…是自然对数的底数)在f(x)的定义域上单调递增，则称函数f(x)具有M性质．下列函数中所有具有M性质的函数的序号为________．

①f(x)＝2－x　②f(x)＝3－x　③f(x)＝x3

④f(x)＝x2＋2.

四     经典大题强化篇

1.[2022·安徽省合肥高三模拟]已知函数f(x)＝x2－ax ln x＋ax.

(1)当a＝1时，判断f(x)的单调性；

(2)若f(x)有两个极值点，求实数a的取值范围．

2．[2022·山西省名校联考]已知函数f(x)＝ex－ax有两个零点x1，x2(x1<x2).

(1)求实数a的取值范围；

(2)证明：x2－x1<－2.