

江苏省苏州市工业园区青剑湖实验中学2023-2024学年九年级上学期段考物理试卷(10月份)
展开2023-2024学年江苏省苏州市工业园区青剑湖实验中学九年级(上)段考物理试卷(10月份)
一、选择题(每小题2分,共24分.请将唯一正确的选项填涂在答题卡相应的位置上)
1.(2分)下列数据中正确的是( )
A.人骑车时的功率大约是80W
B.将地面的足球举过头顶所做的功大约为100J
C.中学生完成一个引体向上所做的功约为1000J
D.机械改进后其效率可达100%
2.(2分)小明在剪纸时,所用剪刀的机械效率为80%,这表示( )
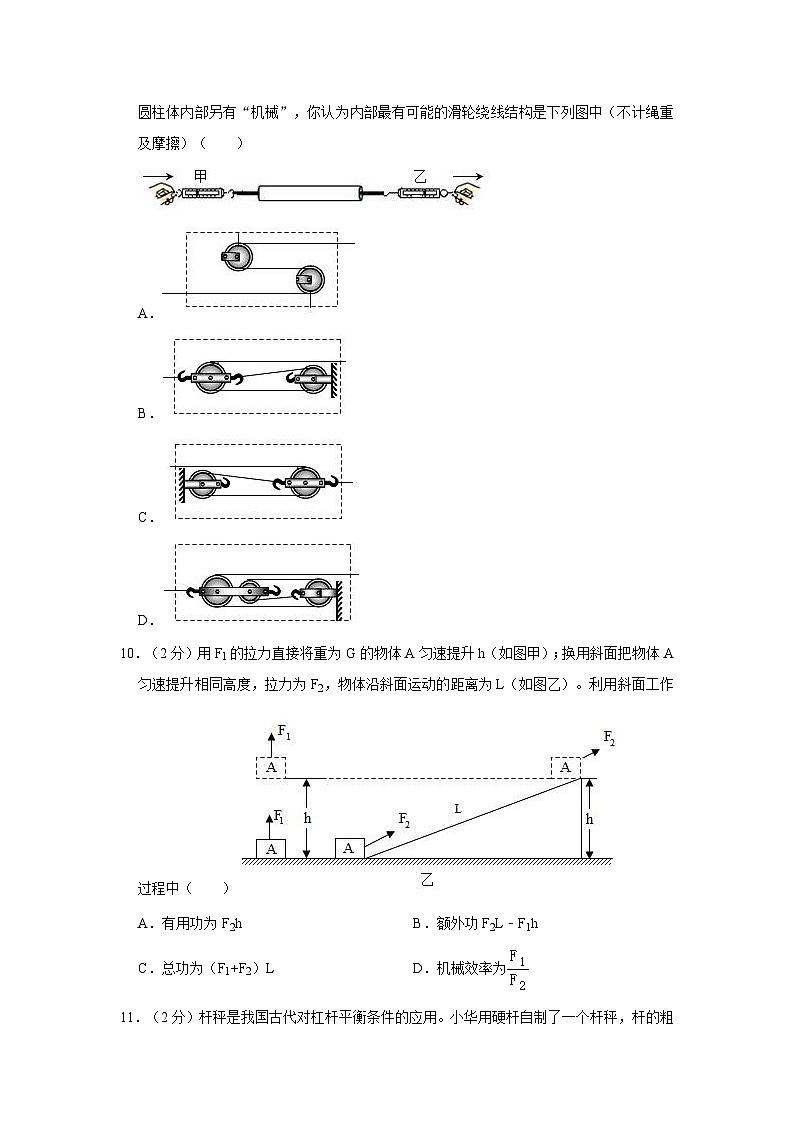
A.若作用在剪刀的动力做功1J,则有0.8J的功用于剪纸
B.若作用在剪刀的动力做功1J,则有0.2J的功用于剪纸
C.若作用在剪刀的动力是1N,则阻力是0.8N
D.若作用在剪刀的阻力是1N,则动力是0.8N
3.(2分)如图所示是农民拔去地里的棉杆工具,使用时,将小铲着地,然后在套管上用力,棉杆就拔出来了。该农具整体视为杠杆( )
A.转轴—虎口—套管 B.虎口—转轴—套管
C.小铲—虎口—套管 D.小铲—套管—虎口
4.(2分)如图所示,某同学用重为10N的动滑轮匀速提升重为50N的物体,不计摩擦( )
A.20N B.25N C.30N D.35N
5.(2分)如图所示,为一可绕O点转动的杠杆,在A端通过绳作用一竖直向下的拉力F使杠杆平衡,保持重物静止不动,而使绳绕A点从如图所示的位置沿图中的虚线CD转动,则( )
A.逆时针转,F先变小后变大
B.顺时针转,F先变小后变大
C.顺时针转,F先变大后变小
D.逆时针转,F先变大后变小
6.(2分)在生产和生活中经常使用各种机械,关于机械的下列说法,正确的是( )
A.使用机械可以省力、省距离,也可以省功
B.机械做功越快,机械效率越高
C.功率越大的机械,做功越快
D.机械做功越多,机械效率越高
7.(2分)如图所示,B端悬挂一重为G的重物,不计杠杆自重( )
A.杠杆可能为等臂杠杆
B.因为OA大于OB,所以F小于G
C.当杠杆平衡时,一定满足G×OB=F×OA
D.动力的方向一定竖直向下
8.(2分)一位体重为500N的同学在跳绳测试中,1min跳180次,每次腾空的最大高度平均为4cm,克服重力做功的平均功率是( )
A.60W B.3.6×103W C.6×103W D.3.6×105W
9.(2分)在我校物理科技节上,玲玲老师给大家演示了神奇的“二力平衡”。如图所示,当一学生握住中间细细的圆柱体并保持静止时,使“整根”细线向右做匀速运动,神奇的是:左手甲弹簧测力计的示数为4.8N,为何细线还能向右匀速运动呢?原来中空的细圆柱体内部另有“机械”,你认为内部最有可能的滑轮绕线结构是下列图中(不计绳重及摩擦)( )
A.
B.
C.
D.
10.(2分)用F1的拉力直接将重为G的物体A匀速提升h(如图甲);换用斜面把物体A匀速提升相同高度,拉力为F2,物体沿斜面运动的距离为L(如图乙)。利用斜面工作过程中( )
A.有用功为F2h B.额外功F2L﹣F1h
C.总功为(F1+F2)L D.机械效率为
11.(2分)杆秤是我国古代对杠杆平衡条件的应用。小华用硬杆自制了一个杆秤,杆的粗细不均匀,将提纽固定在O点,托盘中不放重物,将秤砣移至O点左侧的B点,如图所示。已知提纽与托盘间距离OA=10cm,OB=2cm,以下说法正确的是( )
A.秤的零刻线在O点
B.因杆粗细不均匀,所以秤的刻线分布也不均匀
C.秤的2kg刻度线在O点右侧C处,OC=38cm
D.称量物体质量时,若杆秤右端上扬,可将秤砣向左侧适当移动
12.(2分)小明去健身房用如图所示的牵引装置来锻炼腿部和手部肌肉。使用时,若绳a处固定不动,手在b处需用力Fb拉绳,使重物G匀速上升;若绳b处固定不动a拉绳,使重物G匀速上升。不计绳重和摩擦,则( )
A.Fb=Fa B.Fb=2Fa C.Fb<2Fa D.Fb>2Fa
二、填空题(每空1分,共27分)
13.(4分)杠杆的应用非常广泛,如图所示的两种剪刀,正常使用时属于省力杠杆的是 剪刀(甲/乙);如图所示,A装置是 滑轮(定/动),它的实质是 ,使用它的作用是 。
14.(4分)船桨可看成一根杠杆。如图所示,其支点位于图中 点,要使划船时所用的力小一些,则运动员两只手之间的距离应 一些(选填“增大”、“减小”、“不变”)。船桨属于 杠杆(选填“省力”、“等臂”、“费力”),它的优点是 。
15.(2分)“暴走”是一种快速的徒步运动方式,人体重心约在肚脐处。如图甲所示是人体重心最低的位置,如图乙所示是重心最高位置,他10s内行走了40步,则每走一步克服重力所做的功为 J,功率为 W。(g取10N/kg)
16.(3分)如图所示,滑轮重小于物重(不计绳重和摩擦),若在相同时间内匀速提升相同的重物相同的高度甲 F乙,拉力做功的功率P甲 P乙,机械效率η甲 η乙.(选填“>”、“<”或“=”)。
17.(2分)如图所示,桃子从树上落下的过程中,先后经过A、B、C三点,在经历AB和BC过程中桃子重力做功分别为W1、W2,功率分别为P1、P2,则有W1 W2;P1 P2.(都选填“大于”、“等于”或“小于”)
18.(4分)工人师傅要将质量100kg的木箱搬到1.5m高的车厢里,他将一块5m长的木板搁在地面与车厢之间构成的斜面,然后站在车上用400N的拉力在10s内将物体从斜面底端匀速拉到车厢里,那么工人所做的有用功为 J,工人做功的功率为 W,斜面的机械效率为 ,物体所受摩擦为 N。
19.(3分)如图为一辆变速自行车,它的车把和后轮都可看作是一个杠杆或轮轴;你认为车把是一个 杠杆(或轮轴)(选填“省力”、“费力”或“等臂”),后轮是一个 杠杆(或轮轴)(选填“省力”或“费力”),骑着它爬坡时,后轴的齿轮应更换 。(选填“较大的”或“较小的”)
20.(2分)某轿车以96kW的恒定功率在水平路面启动做直线运动,速度v与时间t的关系如图所示,若轿车运动过程中受到的阻力不变,其发动机做功为 J,运动过程中受到的阻力为 N。
21.(3分)风车是利用风力做功的装置。小明制作了一架小风车,他想粗略测定风车在一定风速下做功的功率,实验装置如图所示。除了图中的实验器材
(1)观察实验装置,小明是通过测量细线对 做功的功率来测定风车做功的功率。
(2)实验时,逐渐增加挂在细线下的回形针数量,直到细线恰好缓慢匀速提升回形针为止。若测得回形针匀速上升的高度h、所用的时间t、回形针的总质量m,则风车做功的功率P= (请用题给符号写出表达式)。
(3)实验过程中,风车转轴处总会有摩擦,摩擦较小时与摩擦较大时相比 (选填:大/小)时测得风车的功率值较大。
三、解答题(本大题共11小题,共49分,其中26、27、28题需有解题过程)
22.(2分)工人沿台阶向上滚动圆柱形塑料桶如图所示。他在A点施加力F使塑料桶绕O点向上滚动,请画出F的力臂。
23.(2分)请在图中画出重物所受重力的示意图,并在杠杆上的B点画出能使杠杆在图示位置保持平衡的最小动力F的示意图。
24.(2分)用滑轮组将放在水平地面上的重物G提起,在图中画出最省力的绳子绕法。
25.(2分)如图,质量分布不均匀的长方形物体放在水平地面上,A点是它的重心,在物体上画出所施加最小力的示意图及其力臂,并标明支点O。
26.(6分)天门山盘山公路是网红打卡地,公路全长大约10km,公路的海拔落差高度约1000m。为提供多元的登山方式,客车满载时总质量为6000kg。现有一辆满载的新能源客车,以100kW的恒定功率(行驶过程中客车所受重力和阻力大小恒定不变,g取10N/kg)请完成下列问题:
(1)整个过程中,电动机对客车和游客所做的有用功为多少?
(2)盘山公路的机械效率为多少?
(3)整个过程中,汽车受到的阻力为多少?
27.(6分)一辆在水平路面上沿直线匀速行驶的货车,行驶时所受的阻力为车总重的0.1倍,货车(含驾驶员)4N。
(1)求货车空载行驶时所受的阻力大小;
(2)求货车以36km/h的速度空载匀速行驶时,10s内货车牵引力做的功;
(3)当货车以90kW的额定功率、90km/h的速度匀速行驶时,求货车最多可装载多重的货物。
28.(6分)玻璃装运车间常用“低压吸盘吊车”进行吊运玻璃,如图甲所示,先将6个吸盘压在玻璃上,在大气压作用下吸盘将玻璃“吸住”,再通过电动机牵引滑轮组自由端的绳子就可以将玻璃吊起。图乙为“低压吸盘吊车”结构示意图,每个滑轮的质量为15kg,不计抽气管和绳重,在某次吊装过程中,吊车将一块重为90kg的玻璃以0.2m/s的速度吊高2m。求:
(1)本次吊装过程中所做的有用功是多少?
(2)本次吊装过程中,电动机拉绳子自由端的拉力做功时的功率为多大?
(3)本次吊装过程中,该装置的机械效率是多少?
29.(8分)如图是探究“杠杆平衡条件”的实验。
(1)如图甲所示,此时杠杆 (处于/不处于)平衡状态;为使杠杆在水平位置平衡应将平衡螺母向 (左/右)调节。
(2)杠杆水平平衡后,小明在杠杆A点处挂上2个钩码,B点处挂上 个钩码,可以再次使杠杆在水平位置平衡,若把A、B处所挂钩码同时向支点移动1格 (选填“依然平衡”“左端下降”或“右端下降”);
(3)小明将一端的钩码换成弹簧测力计,发现按图丙中弹簧测力计使用方式校零时往往很困难,由于弹簧测力计的弹簧和秤钩都有一定的质量 绳子受到的实际拉力(选填“大于”或“小于”),为了在竖直向下方向校零,一种方法是取两个弹簧测力计先竖直方向校零后,秤钩对钩,在竖直方向拉到某一数值 (甲/乙)的指针,使其示数与另一弹簧测力计相等即可完成校零。
(4)实验中小明曾提出“力的作用点到支点的距离影响杠杆的平衡”。为判断这一观点是否正确,小华制作了一个密度均匀的圆盘(相当于杠杆),圆盘可以绕着圆心O转动(转轴阻力忽略不计),又在G点挂上一定数量的钩码后,圆盘在图示位置平衡;接着他将挂在G点的钩码先后挂在 两个点又进行了两次实验,发现圆盘仍在图示位置平衡,则说明小明的观点是 (选填“正确”或“错误”)的。
30.(5分)小华等同学在“测滑轮组机械效率”的实验中得到的数据如表所示,实验装置如图所示。
(1)小华发现实验过程中边拉边读数,弹簧测力计示数不稳定,应该静止读数 (选填“正确”或“不正确”),因为他没有考虑到 对滑轮组机械效率的影响。
实验次数
钩码重力G/N
钩码上升高度h/m
绳端拉力F/N
绳端移动距离s/m
机械效率η
1
2
0.1
1.39
0.2
72%
2
2
0.1
0.90
0.3
74%
3
4
0.1
1.51
0.3
88%
4
4
0.1
1.25
0.4
②
(2)表中第4次实验数据是用 图装置进行实验的,请问表中②的值为 。
(3)通过比较2、3两次实验数据得出结论:同一滑轮组提升重物时,物重越大,滑轮组的机械效率越 。
31.(7分)物理学在桥梁建筑技术方面有很多应用,如图甲为宜兴首座钢结构斜拉桥荆邑大桥,桥梁全长544.5米,有十八层楼那么高。“桥塔为什么要造这么高?”
小华对此进行了研究:他将大桥的结构进行简化,抽象成图乙所示的模型。小华通过比较发现:适当增加桥塔的高度,可 (增大/减小)斜拉索拉力的力臂,从而 (增大/减小)斜拉索的拉力,在桥面上行驶的汽车,位置越靠近桥塔 (大/小)、桥面限速60km/h,在遵守交通规则的前提下,一辆小车通过全桥至少需要 s(结果保留一位小数)。近年来,多起高架桥侧翻事故引起了人们对如图丙所示的独柱高架桥安全性的思考。
独柱式高架桥分如图丁(a)单支座式和图丁(b)双支座式,建造桥梁时应选择的支撑方式为 (单/双)支座式。当重载卡车在双支座式高架桥最右侧行驶时桥面侧翻,支点是 (左/右)支座。如果在两个支座中间再增加一个支座如图丁(c),桥面侧翻危害的风险将 (减小/增大/不变)。
32.(3分)在机械制造中有一个给大飞轮定重心的工序,该工序的目的是使飞轮的重心发生微小的位移,以使它准确位于轴心上。如图所示(图中两虚线的交点)自由转动。用力推动一下大飞轮,飞轮转动若干周后停止。多次试验
(1)根据以上情况,可以初步确定飞轮重心P可能在图中 。
A.轴心正下方的某一位置 B.轴心左侧的某一位置
C.轴心右侧的某一位置 D.轴心正上方的某一位置
(2)工人在飞轮边缘上的某点E处,焊接上质量为m=0.4kg的金属后,再用力推动飞轮 的现象时,说明飞轮的重心已调整到轴心上了。
(3)调整前飞轮的重心P到轴心的距离为 mm。
2023-2024学年江苏省苏州市工业园区青剑湖实验中学九年级(上)段考物理试卷(10月份)
参考答案与试题解析
一、选择题(每小题2分,共24分.请将唯一正确的选项填涂在答题卡相应的位置上)
1.(2分)下列数据中正确的是( )
A.人骑车时的功率大约是80W
B.将地面的足球举过头顶所做的功大约为100J
C.中学生完成一个引体向上所做的功约为1000J
D.机械改进后其效率可达100%
【答案】A
【分析】根据日常生产生活知识,分别计算出选项中数据,然后一一比较即可。
【解答】解:A、人骑自行车的速度v=5m/s左右,骑行功率在P==,故A正确。
B、足球的质量约为450g=0.45kg,从地面到举过头顶的高度约为3m,故B错误;
C、一个中学生的体重约500N,完成一个引体向上所做的功约为:W=Gh=500N×0.5m=250J;
D、使用定滑轮时、克服绳重做额外功,故D错误。
故选:A。
2.(2分)小明在剪纸时,所用剪刀的机械效率为80%,这表示( )
A.若作用在剪刀的动力做功1J,则有0.8J的功用于剪纸
B.若作用在剪刀的动力做功1J,则有0.2J的功用于剪纸
C.若作用在剪刀的动力是1N,则阻力是0.8N
D.若作用在剪刀的阻力是1N,则动力是0.8N
【答案】A
【分析】①使用机械时,人们为完成某项任务必须做的功叫有用功;对完成任务没有用,但又不得不做的功叫额外功;有用功与额外功之和叫总功;有用功与总功的比值,是机械效率。
②机械效率是有用功与总功的比值,与动力或阻力的大小无关。
【解答】解:小明在剪纸时,目的是剪纸,克服摩擦做的功为额外功。
所用剪刀的机械效率为80%,表示若作用在剪刀的动力做功1J。
故选:A。
3.(2分)如图所示是农民拔去地里的棉杆工具,使用时,将小铲着地,然后在套管上用力,棉杆就拔出来了。该农具整体视为杠杆( )
A.转轴—虎口—套管 B.虎口—转轴—套管
C.小铲—虎口—套管 D.小铲—套管—虎口
【答案】D
【分析】杠杆绕着转动的固定点叫支点;
使杠杆转动的力叫动力,动力作用的位置叫动力作用点;
阻碍杠杆转动的力叫阻力,阻力作用的位置叫阻力作用点。
【解答】解:将小铲着地,整个杠杆是绕着小铲转动的;
要让杠杆转动,在套管上用力;
虎口处夹着棉花杆,棉花杆会对虎口处施加一个阻碍杠杆转动的力,
支点、动力作用点、套管。
故选:D。
4.(2分)如图所示,某同学用重为10N的动滑轮匀速提升重为50N的物体,不计摩擦( )
A.20N B.25N C.30N D.35N
【答案】D
【分析】动滑轮有几段绳子承担,拉力就是物体和动滑轮总重的几分之一。
【解答】解:由图可知,物体与滑轮的总重力由两段绳子承担,
所以由力的合成可得:2F>G滑轮+G物=10N+50N=60N,即:F>30N,D正确。
故选:D。
5.(2分)如图所示,为一可绕O点转动的杠杆,在A端通过绳作用一竖直向下的拉力F使杠杆平衡,保持重物静止不动,而使绳绕A点从如图所示的位置沿图中的虚线CD转动,则( )
A.逆时针转,F先变小后变大
B.顺时针转,F先变小后变大
C.顺时针转,F先变大后变小
D.逆时针转,F先变大后变小
【答案】B
【分析】从支点向力的作用线作垂线,垂线段的长度即力臂。根据杠杆平衡条件动力×动力力臂=阻力×阻力力臂,分析力臂的变化可知力的变化。
【解答】解:如右图;连接OA;
已知阻力(物重)不变,阻力臂不变动L动=F阻L阻,知:
在F阻L阻不变的情况下,动力臂越长越省力;
因此以OA为动力臂时,动力F最小;
由图可知:当绳从图示位置沿顺时针方向旋转时,力F先变小后变大。
沿逆时针方向旋转时,力F变大。
故选:B。
6.(2分)在生产和生活中经常使用各种机械,关于机械的下列说法,正确的是( )
A.使用机械可以省力、省距离,也可以省功
B.机械做功越快,机械效率越高
C.功率越大的机械,做功越快
D.机械做功越多,机械效率越高
【答案】C
【分析】要解决此题需要了解:各机械的作用,从机械的利与弊两方面进行分析;机械效率反映有用功占总功的比例或额外功占总功的比例;功率是指做功的快慢。
【解答】解:A、我们使用机械有时是为了省力,有时是为了改变力的方向,故A错误;
B、机械做功越快,但不能说明机械效率越高;
C、功率是表示做功快慢的物理量,做功越快;
D、机械效率反映有用功占总功的比例或额外功占总功的比例,但机械效率不一定越高。
故选:C。
7.(2分)如图所示,B端悬挂一重为G的重物,不计杠杆自重( )
A.杠杆可能为等臂杠杆
B.因为OA大于OB,所以F小于G
C.当杠杆平衡时,一定满足G×OB=F×OA
D.动力的方向一定竖直向下
【答案】A
【分析】(1)因为在A点施加动力F的方向不知道,所以力F的力臂可能比OB大,也可能比OB小,还可能相等,力F的力臂大小决定了F与G的大小关系;
(2)力F的作用与G的作用应使杠杆向两个相反的方向旋转。
【解答】解:
ABC、因为力F的方向不确定,则不一定满足G×OB=F×OA;
力F的方向不确定,则力F的力臂可能大于或小于或等于G的力臂;故A正确。
D、杠杆平衡时,由图知F的方向应向下,故D错误;
故选:A。
8.(2分)一位体重为500N的同学在跳绳测试中,1min跳180次,每次腾空的最大高度平均为4cm,克服重力做功的平均功率是( )
A.60W B.3.6×103W C.6×103W D.3.6×105W
【答案】A
【分析】已知该同学的体重和每次腾空的高度,则可利用公式W=Gh计算每跳一次克服重力做的功,跳了180次,从而可以求出他在跳绳过程中克服重力做的功,已知时间,可利用公式P=计算做功的功率。
【解答】解:
∵G=500N,h=4cm=0.04m,
∴跳一次克服重力做功为:W=Gh=500N×3.04m=20J,
1min跳180次所做的总功为:W总=180×20J=3600J,
又∵t=1min=60s,
∴功率为:P===60W。
故选:A。
9.(2分)在我校物理科技节上,玲玲老师给大家演示了神奇的“二力平衡”。如图所示,当一学生握住中间细细的圆柱体并保持静止时,使“整根”细线向右做匀速运动,神奇的是:左手甲弹簧测力计的示数为4.8N,为何细线还能向右匀速运动呢?原来中空的细圆柱体内部另有“机械”,你认为内部最有可能的滑轮绕线结构是下列图中(不计绳重及摩擦)( )
A.
B.
C.
D.
【答案】B
【分析】首先根据左手甲弹簧测力计的示数为4.8N,右手乙弹簧测力计的示数却只有1.6N,可确定绳子的股数,其次明确使用滑轮组时,不计绳重和摩擦,动滑轮的绳子有几段,所用的力就是摩擦力和动滑轮重的几分之一;然后对各个选项注意分析即可。
【解答】解:由“左手甲弹簧测力计的示数为4.8N,右手乙弹簧测力计的示数却只有2.6N”可知,F乙=F甲,由此可确定内部的滑轮的绕线是三段绳子,A选项是两个定滑轮。B是三段绳子承担。C选项应该是B的颠倒。
故选:B。
10.(2分)用F1的拉力直接将重为G的物体A匀速提升h(如图甲);换用斜面把物体A匀速提升相同高度,拉力为F2,物体沿斜面运动的距离为L(如图乙)。利用斜面工作过程中( )
A.有用功为F2h B.额外功F2L﹣F1h
C.总功为(F1+F2)L D.机械效率为
【答案】B
【分析】直接将物体提起做的功为有用功,利用斜面拉力做的功为总功,总功等于有用功加上额外功,利用η=求斜面的机械效率。
【解答】解:
如图甲,F1做的功为直接提升物体做的功,
则利用斜面做的有用功:W有=Gh=F1h,
利用斜面做的总功:W总=F7L,
利用斜面做的额外功:
W额=W总﹣W有用=F2L﹣F1h,
斜面的机械效率:
η==,
可见,ACD错。
故选:B。
11.(2分)杆秤是我国古代对杠杆平衡条件的应用。小华用硬杆自制了一个杆秤,杆的粗细不均匀,将提纽固定在O点,托盘中不放重物,将秤砣移至O点左侧的B点,如图所示。已知提纽与托盘间距离OA=10cm,OB=2cm,以下说法正确的是( )
A.秤的零刻线在O点
B.因杆粗细不均匀,所以秤的刻线分布也不均匀
C.秤的2kg刻度线在O点右侧C处,OC=38cm
D.称量物体质量时,若杆秤右端上扬,可将秤砣向左侧适当移动
【答案】C
【分析】杆秤利用的是杠杆的平衡条件,通过力臂的大小关系得出物体重和秤砣重之间的关系,进而得出物体的质量与秤砣的质量之间的关系,测量的是物体的质量。
【解答】解:A、将提纽固定在O点,托盘中不放重物,秤杆可以在水平位置平衡,故A错误;
B、无论杆秤粗细是否均匀,因为无论杆秤粗细是否均匀1L1=F8L2可知,动力臂与阻力的大小成正比;
C、由题意知B点为零刻度线,OB=2cm,
利用支点左端力与力臂乘积的变化量等于右端力与力臂乘积变化量:m6g×OA﹣m2×OB=m2g×OC,
即8kg×10N/kg×10cm﹣0.5kg×10N/kg×7cm=0.5kg×10N/kg×OC,
解得:OC=38cm,故C正确;
D、秤杆右端上扬,应将秤砣向右移,故D错误。
故选:C。
12.(2分)小明去健身房用如图所示的牵引装置来锻炼腿部和手部肌肉。使用时,若绳a处固定不动,手在b处需用力Fb拉绳,使重物G匀速上升;若绳b处固定不动a拉绳,使重物G匀速上升。不计绳重和摩擦,则( )
A.Fb=Fa B.Fb=2Fa C.Fb<2Fa D.Fb>2Fa
【答案】D
【分析】(1)当绳b处固定不动,在a处用力Fa拉绳时,该图中滑轮均为定滑轮,不计绳重和摩擦,根据定滑轮不省力只改变力的方向可知绳a处的拉力Fa;
(2)由图可知,当绳a处固定不动,手在b处用力Fb拉绳时,a处的拉力和物体的重力G相等,物体G匀速上升时中间的滑轮处于平衡状态,根据二力平衡可知绳b处的拉力Fb。
【解答】解:(1)当绳b处固定不动,在a处用力Fa拉绳时,该图中所有滑轮均为定滑轮,则Fa=G;
(2)由图知,当绳a处固定不动b拉绳时,a处的拉力F拉和物体的重力G相等,
物体G匀速上升时,中间的滑轮处于平衡状态,
不计绳重和摩擦,中间的滑轮受向上的拉力Fb、2段绳子向下的拉力2F拉和中间滑轮向下的重力G动,
则由二力平衡条件可得:
Fb=7F拉+G动=2G+G动>2Fa;
即6Fa<Fb。
故选:D。
二、填空题(每空1分,共27分)
13.(4分)杠杆的应用非常广泛,如图所示的两种剪刀,正常使用时属于省力杠杆的是 甲 剪刀(甲/乙);如图所示,A装置是 定 滑轮(定/动),它的实质是 等臂杠杆 ,使用它的作用是 改变用力的方向 。
【答案】甲;定;等臂杠杆;改变用力的方向。
【分析】(1)剪刀属于杠杆,根据使用时动力臂与阻力臂的大小关系确定杠杆类型;
(2)定滑轮的本质是等臂杠杆,既不省力也不费力,但是可以改变力的方向。
【解答】解:(1)甲剪刀使用时,动力臂大于阻力臂;乙剪刀使用时,为费力杠杆。
(2)A装置的轴不能随物体一起移动,是定滑轮,使用定滑轮不省力。
故答案为:甲;定;等臂杠杆。
14.(4分)船桨可看成一根杠杆。如图所示,其支点位于图中 A 点,要使划船时所用的力小一些,则运动员两只手之间的距离应 增大 一些(选填“增大”、“减小”、“不变”)。船桨属于 费力 杠杆(选填“省力”、“等臂”、“费力”),它的优点是 省距离 。
【答案】A;增大;费力;省距离。
【分析】结合图片和生活经验,判断船桨在使用过程中,动力臂和阻力臂的大小关系便可以知道是省力还是费力,由杠杆平衡条件便可知如何能够更省力。
【解答】解:如图,在使用船桨时,动力作用点在B点;
使划船时所用的力小一些,由杠杆平衡条件:F1×L1=F4×L2,要使动力减小,在阻力和阻力臂不变的条件下,也就是增大两只手之间的距离;
船桨在使用时,动力臂小于阻力臂费力。
故答案为:A;增大;省距离。
15.(2分)“暴走”是一种快速的徒步运动方式,人体重心约在肚脐处。如图甲所示是人体重心最低的位置,如图乙所示是重心最高位置,他10s内行走了40步,则每走一步克服重力所做的功为 25 J,功率为 100 W。(g取10N/kg)
【答案】25;100。
【分析】(1)根据直角三角形的特征利用勾股定理求出重心升高的高度,再利用公式W=Gh求出每走一步克服重力所做的功;
(2)先求出10s内行走了40步克服重力所做的总功,再利用P=求出克服重力做功的功率。
【解答】(1)重心升高的高度h=65cm﹣=6cm=0.05m;
小明每走一步克服重力所做的功:W=Gh=mgh=50kg×10N/kg×0.05m=25J;
(4)他10s内行走了40步克服重力所做的总功为:
W总=40W=40×25J=1000J;
则克服重力做功的功率为:P=。
故答案为:25;100。
16.(3分)如图所示,滑轮重小于物重(不计绳重和摩擦),若在相同时间内匀速提升相同的重物相同的高度甲 > F乙,拉力做功的功率P甲 < P乙,机械效率η甲 > η乙.(选填“>”、“<”或“=”)。
【答案】见试题解答内容
【分析】(1)动滑轮和定滑轮的使用特点:使用定滑轮不能省力,但能改变动力的方向;使用动滑轮不能改变动力的方向,但能省力。
(2)根据公式P=可比较功率的大小;
(3)比较有用功和总功的大小,根据机械效率公式η=分析机械效率大小。
【解答】解:
(1)甲图是一个定滑轮,定滑轮不能省力,因此F甲=G;
乙图是一个动滑轮,且动滑轮重小于物重,
不计绳重和摩擦,则F乙=(G动+G)<G;所以F甲>F乙。
(2)用定滑轮和动滑轮分别将质量相同的甲、乙两物体匀速提升相同的高度有=Gh=mgh可知,则所做的有用功一样大;
使用动滑轮时,由于要克服动滑轮的重力做额外功,即拉力做功W甲<W乙;已知做功时间相同,根据公式P=,使用动滑轮时拉力做功的功率大甲<P乙;
(3)由前面分析可知,使用定滑轮和动滑轮时所做的有用功相同,根据机械效率的公式η=,动滑轮的机械效率低甲>η乙。
故答案为:>;<;>。
17.(2分)如图所示,桃子从树上落下的过程中,先后经过A、B、C三点,在经历AB和BC过程中桃子重力做功分别为W1、W2,功率分别为P1、P2,则有W1 等于 W2;P1 小于 P2.(都选填“大于”、“等于”或“小于”)
【答案】见试题解答内容
【分析】(1)比较两个阶段的重力和距离,根据W=Gh比较两个阶段的重力做功大小。
(2)物体在下落过程中重力势能不断转化为动能,速度不断增大,比较两个阶段的运动时间,根据P=比较功率。
【解答】解:(1)因为AB=BC,重力相同,重力做功相同1=W2。
(2)因为桃子在自由下落时做加速运动,即在BC段的运动速度大于AB段的运动速度可知,
又由P=可知,即P5<P2。
故答案为:等于;小于。
18.(4分)工人师傅要将质量100kg的木箱搬到1.5m高的车厢里,他将一块5m长的木板搁在地面与车厢之间构成的斜面,然后站在车上用400N的拉力在10s内将物体从斜面底端匀速拉到车厢里,那么工人所做的有用功为 1500 J,工人做功的功率为 200 W,斜面的机械效率为 75% ,物体所受摩擦为 100 N。
【答案】见试题解答内容
【分析】(1)知道木箱的重力和斜面的高度,根据W=Gh求出克服重力做的有用功;
(2)已知拉力F与斜面长,利用W=Fs计算总功,根据公式P=计算功率;
(3)知道有用功和总功,根据机械效率公式求出机械效率。
(4)总功减去有用功即为克服摩擦力所做的额外功,根据W额=fs求出物体和斜面之间的摩擦力。
【解答】解:(1)木箱的重力:
G=mg=100kg×10N/kg=1000N,
工人师傅对木箱做的有用功:
W有用=Gh=1000N×1.5m=1500J;
(2)拉力做的总功:
W总=Fs=400N×7m=2000J。
拉力做功的功率为:
P总===200W。
(3)斜面的机械效率:
η=×100%=。
(4)克服摩擦力所做的额外功:
W额=W总﹣W有=2000J﹣1500J=500J,
由W额=fs可得,物体和斜面之间的摩擦力:
f===100N。
故答案为:1500;200;100。
19.(3分)如图为一辆变速自行车,它的车把和后轮都可看作是一个杠杆或轮轴;你认为车把是一个 省力 杠杆(或轮轴)(选填“省力”、“费力”或“等臂”),后轮是一个 费力 杠杆(或轮轴)(选填“省力”或“费力”),骑着它爬坡时,后轴的齿轮应更换 较大的 。(选填“较大的”或“较小的”)
【答案】见试题解答内容
【分析】轮轴由轮和轴组成,是变形杠杆,动力作用在轮上可以省力,作用在轴上费力。
【解答】解:车把在使用时是轮轴,在轮上用力是一个省力轮轴,由于动力作用在轴上;
骑着它爬坡时,后轴的齿轮应更换较大的,齿轮越大,爬坡更容易一些。
故答案为:省力;费力。
20.(2分)某轿车以96kW的恒定功率在水平路面启动做直线运动,速度v与时间t的关系如图所示,若轿车运动过程中受到的阻力不变,其发动机做功为 1.92×105 J,运动过程中受到的阻力为 3.2×103 N。
【答案】1.92×105;3.2×103。
【分析】(1)轿车的功率恒定,根据P=求出发动机在0~2s时间内做的功;
(2)根据图像可知轿车在15s以后做匀速直线运动,根据P===Fv求出发动机的牵引力,根据二力平衡条件求出轿车在运动过程中受到的阻力。
【解答】解:(1)轿车的功率恒定为P=96kW,由P=,发动机在0~2s时间内做的功为:W=Pt=96×103W×2s=1.92×103J;
(2)由图像可知,轿车在15s以后做匀速直线运动,
由P===Fv可知==3.8×103N,
因为此过程中轿车做匀速直线运动,所以,轿车运动过程中受到的阻力:f=F=3.4×103N。
故答案为:1.92×106;3.2×107。
21.(3分)风车是利用风力做功的装置。小明制作了一架小风车,他想粗略测定风车在一定风速下做功的功率,实验装置如图所示。除了图中的实验器材
(1)观察实验装置,小明是通过测量细线对 回形针 做功的功率来测定风车做功的功率。
(2)实验时,逐渐增加挂在细线下的回形针数量,直到细线恰好缓慢匀速提升回形针为止。若测得回形针匀速上升的高度h、所用的时间t、回形针的总质量m,则风车做功的功率P= (请用题给符号写出表达式)。
(3)实验过程中,风车转轴处总会有摩擦,摩擦较小时与摩擦较大时相比 小 (选填:大/小)时测得风车的功率值较大。
【答案】(1)回形针;(2);(3)小。
【分析】(1)由图可知,回形针随风车的转动会上升,测量细线对回形针做功的功率即可测出风车做功的功率;
(2)根据做功公式和功率公式得出细线对回形针做功的功率即为风车做功功率的表达式;
(3)风速一定时,总能量不变,根据能量的转化分析测得风车的功率值如何变化。
【解答】解:
(1)由实验装置可知,回形针随风车的转动会上升,这用到了转换法;
(2)若测得回形针匀速上升的高度h、所用的时间t,则风车做功的功率:P===;
(3)风速一定时,总能量不变,摩擦较小时克服风车转轴处摩擦消耗的能量小,所以测得风车的功率值会大于摩擦较大时的功率值。
故答案为:(1)回形针;(2)。
三、解答题(本大题共11小题,共49分,其中26、27、28题需有解题过程)
22.(2分)工人沿台阶向上滚动圆柱形塑料桶如图所示。他在A点施加力F使塑料桶绕O点向上滚动,请画出F的力臂。
【答案】见试题解答内容
【分析】力臂是支点到力的作用线的距离;由支点向力的作用线作垂线,垂线段的长度即为力臂。
【解答】解:
图中O为支点,反向延长力F画出F的作用线,该垂线段即为力F的力臂L
23.(2分)请在图中画出重物所受重力的示意图,并在杠杆上的B点画出能使杠杆在图示位置保持平衡的最小动力F的示意图。
【答案】
【分析】重力和作用点在重心,重力的方向竖直向下。
若在杠杆上A端施加最小的力F,使杠杆在水平位置平衡,该力的方向应该垂直杠杆向上,使动力臂最长,在阻力和阻力臂一定时,动力臂最长时、最省力,据此画出动力方向。
【解答】解:根据重力的作用点在重心,重力的方向竖直向下;
为使拉力最小,动力臂要最长,动力臂为OB最长
。
24.(2分)用滑轮组将放在水平地面上的重物G提起,在图中画出最省力的绳子绕法。
【答案】见试题解答内容
【分析】要使滑轮组省力,就是使最多的绳子段数来承担动滑轮的拉力,图中滑轮组由一个动滑轮和一个定滑轮组成,有两种绕线方法。若n为偶数,绳子固定端在定滑轮上;若n为奇数,绳子固定端在动滑轮上;即:“奇动偶定”。
【解答】解:n为奇数时,承担物重的有3段绳子,根据奇动偶定,如图所示:
25.(2分)如图,质量分布不均匀的长方形物体放在水平地面上,A点是它的重心,在物体上画出所施加最小力的示意图及其力臂,并标明支点O。
【答案】见试题解答内容
【分析】①在杠杆上,支点指的是杠杆绕着转动的点;
②根据杠杆的平衡条件,动力臂越长越省力,首先确定出最长的力臂,然后画出的示意图;由支点到力的作用点的距离是最长的力臂。
【解答】解:由图可知,A点是长方体的重心,阻力臂最短,动力最小,最小动力的方向斜向右上方
26.(6分)天门山盘山公路是网红打卡地,公路全长大约10km,公路的海拔落差高度约1000m。为提供多元的登山方式,客车满载时总质量为6000kg。现有一辆满载的新能源客车,以100kW的恒定功率(行驶过程中客车所受重力和阻力大小恒定不变,g取10N/kg)请完成下列问题:
(1)整个过程中,电动机对客车和游客所做的有用功为多少?
(2)盘山公路的机械效率为多少?
(3)整个过程中,汽车受到的阻力为多少?
【答案】(1)整个过程中,电动机对客车和游客所做的有用功为6×107J;
(2)盘山公路的机械效率为30%;
(3)整个过程中,汽车受到的阻力为1.4×104N。
【分析】(1)已知客车满载时总质量,由G=mg可求得其总重力,由W有用=Gh可求得电动机对客车和游客所做的有用功;
(2)已知速度和公路全长可求得时间,已知以80kW的恒定功率匀速行驶至山顶,由W=Pt可求得总功,由η=×100%可求得盘山公路的机械效率;
(3)由W额=W总﹣W有用可求得额外功,由W额=fs可求得汽车受到的阻力。
【解答】解:(1)客车和游客总重力G=mg=6000kg×10N/kg=6×104N;
电动机对客车和游客所做的有用功:W有用=Gh=2×104N×1000m=6×102J;
(2)由v=可得==2×105s,
由P=可得总=Pt=100×103W×2×108s=2×108J,
盘山公路的机械效率:η=×100%=;
(3)额外功:W额=W总﹣W有用=2×108J﹣6×107J=4.4×108J,
由W额=fs可得,汽车受到的阻力:f==4N。
答:(1)整个过程中,电动机对客车和游客所做的有用功为4×107J;
(2)盘山公路的机械效率为30%;
(3)整个过程中,汽车受到的阻力为1.5×104N。
27.(6分)一辆在水平路面上沿直线匀速行驶的货车,行驶时所受的阻力为车总重的0.1倍,货车(含驾驶员)4N。
(1)求货车空载行驶时所受的阻力大小;
(2)求货车以36km/h的速度空载匀速行驶时,10s内货车牵引力做的功;
(3)当货车以90kW的额定功率、90km/h的速度匀速行驶时,求货车最多可装载多重的货物。
【答案】见试题解答内容
【分析】(1)知道货车空载时重G,利用f=0.1G求货车空载行驶时所受的阻力大小;
(2)知道货车空载时速度和行驶时间,利用s=vt求行驶路程,汽车匀速行驶牵引力F=f,再利用W=Fs求10s内货车牵引力做的功;
(3)利用P=Fv求牵引力大小,而汽车匀速行驶时f=F,可求阻力大小,再根据f=0.1G求货车总重,货车最多可装载货物的重等于货车总重减去空车重,再求货物质量。
【解答】解:
(1)货车空载行驶时所受的阻力大小:
f=0.1G=6.1×2.3×104N=2.6×103N;
(2)v=36km/h=36×m/s=10m/s,
∵v=,
10s行驶的路程:
s=vt=10m/s×10s=100m,
∵汽车匀速行驶,
∴牵引力:
F=f=2.8×103N,
10s内货车牵引力做的功:
W=Fs=2.6×103N×100m=2.3×105J;
(3)∵P=F′v′,v′=90km/h=90×,
∴此时牵引力:
F′===3600N,
∵汽车匀速行驶,
∴此时汽车受到的阻力:
f′=F′=3600N,
∵f=0.2G,
∴货车总重:
G′===3.8×104N,
货车最多可装载货物的重力:
G货=G′﹣G=3.7×104N﹣2.6×104N=1.2×104N。
(1)货车空载行驶时所受的阻力大小为2.5×103N;
(2)货车以36km/h的速度空载匀速行驶时,10s内货车牵引力做的功为2.4×105J;
(3)货车最多可装载1.8×104N的货物。
28.(6分)玻璃装运车间常用“低压吸盘吊车”进行吊运玻璃,如图甲所示,先将6个吸盘压在玻璃上,在大气压作用下吸盘将玻璃“吸住”,再通过电动机牵引滑轮组自由端的绳子就可以将玻璃吊起。图乙为“低压吸盘吊车”结构示意图,每个滑轮的质量为15kg,不计抽气管和绳重,在某次吊装过程中,吊车将一块重为90kg的玻璃以0.2m/s的速度吊高2m。求:
(1)本次吊装过程中所做的有用功是多少?
(2)本次吊装过程中,电动机拉绳子自由端的拉力做功时的功率为多大?
(3)本次吊装过程中,该装置的机械效率是多少?
【答案】(1)本次吊装过程中所做的有用功是1800J;
(2)本次吊装过程中,电动机拉绳子自由端的拉力做功时的功率为300W;
(2)在本次吊装过程中,吊车上的滑轮组的机械效率为60%。
【分析】(1)利用G=mg求玻璃的重力G,利用W=Gh求得吊装过程中所做的有用功;
(2)利用G=mg求吸盘、支架和动滑轮的总重力G动总,由图可知n=2,绳子自由端的速度v=nv物,利用不计抽气管和绳重,利用不计绳子与滑轮的摩擦时F=(G+G动总)求绳子自由端的拉力,最后根据P===Fv求拉力所做总功的功率;
(3)利用不计抽气管和绳重,不计绳子与滑轮的摩擦时η====求滑轮组的机械效率。
【解答】解:(1)一块玻璃的重力:
G=mg=90kg×10N/kg=900N,
则吊装过程中所做的有用功是W=Gh=900N×2m=1800J;
(2)吸盘、支架和动滑轮的总重力:
G动总=(m架+m动)g=(45kg+15kg)×10N/kg=600N,
由图可知n=2,绳子自由端的速度:
v=nv物=3×0.2m/s=3.4m/s,
因为不计抽气管和绳重,利用不计绳子与滑轮的摩擦
F=(G+G动总)=(600N+900N)=750N,
则拉力做功的功率:P===Fv=750N×0.6m/s=300W;
(3)因为不计抽气管和绳重,不计绳子与滑轮的摩擦
η======60%。
答:(1)本次吊装过程中所做的有用功是1800J;
(2)本次吊装过程中,电动机拉绳子自由端的拉力做功时的功率为300W;
(2)在本次吊装过程中,吊车上的滑轮组的机械效率为60%。
29.(8分)如图是探究“杠杆平衡条件”的实验。
(1)如图甲所示,此时杠杆 处于 (处于/不处于)平衡状态;为使杠杆在水平位置平衡应将平衡螺母向 右 (左/右)调节。
(2)杠杆水平平衡后,小明在杠杆A点处挂上2个钩码,B点处挂上 1 个钩码,可以再次使杠杆在水平位置平衡,若把A、B处所挂钩码同时向支点移动1格 右端下降 (选填“依然平衡”“左端下降”或“右端下降”);
(3)小明将一端的钩码换成弹簧测力计,发现按图丙中弹簧测力计使用方式校零时往往很困难,由于弹簧测力计的弹簧和秤钩都有一定的质量 小于 绳子受到的实际拉力(选填“大于”或“小于”),为了在竖直向下方向校零,一种方法是取两个弹簧测力计先竖直方向校零后,秤钩对钩,在竖直方向拉到某一数值 乙 (甲/乙)的指针,使其示数与另一弹簧测力计相等即可完成校零。
(4)实验中小明曾提出“力的作用点到支点的距离影响杠杆的平衡”。为判断这一观点是否正确,小华制作了一个密度均匀的圆盘(相当于杠杆),圆盘可以绕着圆心O转动(转轴阻力忽略不计),又在G点挂上一定数量的钩码后,圆盘在图示位置平衡;接着他将挂在G点的钩码先后挂在 ND 两个点又进行了两次实验,发现圆盘仍在图示位置平衡,则说明小明的观点是 错误 (选填“正确”或“错误”)的。
【答案】(1)处于;右;(2)1,右端下降;(3)小于;乙;(4)ND;错误。
【分析】(1)杠杆静止不动或匀速转动叫杠杆的平衡;杠杆右端偏高,说明杠杆的重心在支点左侧,应将平衡螺母向右调节;
(2)设每个钩码重为G,杠杆每格长为L,根据杠杆平衡条件进行分析;
(3))由于弹簧测力计的弹簧和秤钩都有一定的质量,据此分析;由于物体间力的作用是相互的甲对乙的拉力等于乙对甲的拉力;
(4)由题意知,左边力与力臂保持不变,右边力也保持不变,要使圆盘仍然平衡,则右边的力臂也必须保持不变,从而找到另外挂钩码的点。
【解答】解:(1)如图甲所示,此时杠杆静止;为使杠杆在水平位置平衡;
(2)设每个钩码重为G,杠杆每格长为L,2G×2L=nG×8L,故应在B点挂1个钩码才能使杠杆平衡;
当杠杆平衡后,将A,则有2G×L<G×5L;
(3)如图丙所示,在探究杠杆平衡条件实验时,由于弹簧测力计的弹簧和秤钩都有一定的质量,故这时弹簧测计的示数略小于绳子受到的实际拉力;
为了在竖直向下方向校零,一种方法是取两弹簧测力计先竖直方向校零后,物体间力的作用是相互的,因甲测力计已调零,使其示数与甲弹簧测力计相等即可完成校零;
(4)由题意可知,左右两边对圆盘的拉力不变,根据杠杆的平衡条件:F1L1=F2L2得,要使圆盘平衡,所以可以将挂在G点的钩码先后挂在D,这样右边的力臂始终为OD,力的作用点到支点的距离发生变化,故小明的观点是错误的。
故答案为:(1)处于;右;(2)1;(3)小于;乙;错误。
30.(5分)小华等同学在“测滑轮组机械效率”的实验中得到的数据如表所示,实验装置如图所示。
(1)小华发现实验过程中边拉边读数,弹簧测力计示数不稳定,应该静止读数 不正确 (选填“正确”或“不正确”),因为他没有考虑到 摩擦 对滑轮组机械效率的影响。
实验次数
钩码重力G/N
钩码上升高度h/m
绳端拉力F/N
绳端移动距离s/m
机械效率η
1
2
0.1
1.39
0.2
72%
2
2
0.1
0.90
0.3
74%
3
4
0.1
1.51
0.3
88%
4
4
0.1
1.25
0.4
②
(2)表中第4次实验数据是用 丁 图装置进行实验的,请问表中②的值为 80% 。
(3)通过比较2、3两次实验数据得出结论:同一滑轮组提升重物时,物重越大,滑轮组的机械效率越 大 。
【答案】(1)不正确;摩擦;(2)丁;80%;(3)大。
【分析】(1)在“探究影响滑轮组机械效率的因素”的实验中,要匀速竖直向上拉动弹簧测力计,这样示数稳定,便于读数。在测力计静止时,不会克服轮与轴、绳与轮之间的摩擦,据此分析考虑;
(2)根据绳端移动距离与物体升高的高度的关系s=nh求解;根据机械效率公式η==×100%求解;
(3)通过比较2、3两次实验数据,找出相同的量和不同量,分析得出滑轮组的机械效率与变化量的关系。
【解答】解:(1)如果在弹簧测力计静止时读出了数据,由于不会克服轮与轴,所以测力计示数偏小;
(2)丁图中,绳子的有效段数为n=4
s=nh=4×8.1m=0.4m,
表中第4次实验数据是用丁图装置进行实验的;
滑轮组的机械效率:
η===×100%=80%;
(3)通过比较2、5两次实验数据知,重力越大,即同一滑轮组提升重物时,滑轮组的机械效率越高。
故答案为:(1)不正确;摩擦;80%。
31.(7分)物理学在桥梁建筑技术方面有很多应用,如图甲为宜兴首座钢结构斜拉桥荆邑大桥,桥梁全长544.5米,有十八层楼那么高。“桥塔为什么要造这么高?”
小华对此进行了研究:他将大桥的结构进行简化,抽象成图乙所示的模型。小华通过比较发现:适当增加桥塔的高度,可 增大 (增大/减小)斜拉索拉力的力臂,从而 减小 (增大/减小)斜拉索的拉力,在桥面上行驶的汽车,位置越靠近桥塔 小 (大/小)、桥面限速60km/h,在遵守交通规则的前提下,一辆小车通过全桥至少需要 32.7 s(结果保留一位小数)。近年来,多起高架桥侧翻事故引起了人们对如图丙所示的独柱高架桥安全性的思考。
独柱式高架桥分如图丁(a)单支座式和图丁(b)双支座式,建造桥梁时应选择的支撑方式为 双 (单/双)支座式。当重载卡车在双支座式高架桥最右侧行驶时桥面侧翻,支点是 右 (左/右)支座。如果在两个支座中间再增加一个支座如图丁(c),桥面侧翻危害的风险将 不变 (减小/增大/不变)。
【答案】增大;减小;小;32.7;双;右;不变。
【分析】(1)根据杠杆的力臂和杠杆的平衡条件来进行分析。
(2)根据速度公式进行计算。
(3)根据杠杆的五要素和杠杆的平衡条件来分析。
【解答】解:根据图乙可知:在桥的程度一定时,桥塔越高,根据杠杆的平衡条件可知:在阻力和阻力臂一定时。
小华通过比较发现:适当增加桥塔的高度,可增大斜拉索拉力的力臂,在桥面上行驶的汽车,阻力臂越小,钢索受到的拉力越小。
桥面限速60km/h,在遵守交通规则的前提下;
从桥梁的稳定性角度考虑,建造桥梁时应选择的支撑方式为双支座式,支点是右支座,增大了支撑面。
故答案为:增大;减小;小;双;右;不变。
32.(3分)在机械制造中有一个给大飞轮定重心的工序,该工序的目的是使飞轮的重心发生微小的位移,以使它准确位于轴心上。如图所示(图中两虚线的交点)自由转动。用力推动一下大飞轮,飞轮转动若干周后停止。多次试验
(1)根据以上情况,可以初步确定飞轮重心P可能在图中 A 。
A.轴心正下方的某一位置 B.轴心左侧的某一位置
C.轴心右侧的某一位置 D.轴心正上方的某一位置
(2)工人在飞轮边缘上的某点E处,焊接上质量为m=0.4kg的金属后,再用力推动飞轮 每次推动飞轮后,飞轮边缘上的标记F可以停在任意位置 的现象时,说明飞轮的重心已调整到轴心上了。
(3)调整前飞轮的重心P到轴心的距离为 3 mm。
【答案】见试题解答内容
【分析】(1)转动物体静止时,重心应在最低处,由题目中的条件可确定出重心的大致位置。
(2)若重心在转轴处,则物体最后静止时F可在任意点,由此可知答案;
(3)飞轮能停在任意位置,设转到焊接点与重心处在同一水平面上时,焊接物与重心的力矩应当平衡,则由力矩平衡可求得重心的位置。
【解答】解:(1)重心在最低点时,飞轮才能静止,则说明重心应在轴心的正下方;
(2)如果重心在轴心处,则停止时,即F可能出现在任意位置,飞轮边缘上的标记F可以停在任意位置;
(3)考虑到调整后,飞轮可以停在任意位置,
那么当飞轮的重心P和焊接点E转动到同一水平线上时(如图所示),
根据杠杆平衡条件:Mgl=mgR,
解得:l===3×10﹣8m=3mm;
故答案为:(1)A;(2)每次推动飞轮后;(3)3。
江苏省工业园区青剑湖学校2023-2024学年九年级物理第一学期期末监测模拟试题含答案: 这是一份江苏省工业园区青剑湖学校2023-2024学年九年级物理第一学期期末监测模拟试题含答案,共13页。
江苏省工业园区青剑湖学校2023-2024学年物理八上期末调研试题含答案: 这是一份江苏省工业园区青剑湖学校2023-2024学年物理八上期末调研试题含答案,共13页。试卷主要包含了考生必须保证答题卡的整洁,下列数据最符合实际情况的是等内容,欢迎下载使用。
江苏省苏州市工业园区青剑湖实验中学2023-2024学年八年级上学期月考物理试卷(10月份): 这是一份江苏省苏州市工业园区青剑湖实验中学2023-2024学年八年级上学期月考物理试卷(10月份),共31页。试卷主要包含了下列数据中,符合实际情况的是,如图所示是电冰箱工作原理图等内容,欢迎下载使用。












