
广东省佛山市南海区南海实验中学2023-2024学年九年级上学期月考数学试题(无答案)
展开2023—2024学年数学科
一、选择题(10个题,每题3分,共30分)
1.下列方程是一元二次方程的是( )
A. B. C. D.
2.用配方法解方程时,配方结果正确的是( )
A. B. C. D.
3.下列性质中,矩形具有而菱形不一定具有的是( )
A.对边平行 B.对角线相等 C.对角相等 D.中心对称图形
4.根据下列表格,判断方程(,a,b,c为常数)一个根x的范围是( )
x | 3.23 | 3.24 | 3.25 | 3.26 |
0.03 | 0.09 |
A. B. C. D.
5.菱形ABCD的两条对角线长分别为6和10,则该菱形的面积为( )
A.12 B.24 C.30 D.36
6.已知关于x的一元二次方程有实数根,则a的取值范围是( )
A. B. C.且 D.且
7.某个三角形的两边长分别为4和7,第三边的长是方程的根,则这个三角形的周长是( )
A.6 B.13 C.17 D.13或17
8.如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的处,若,则等于( )
A.48° B.57° C.60° D.66°
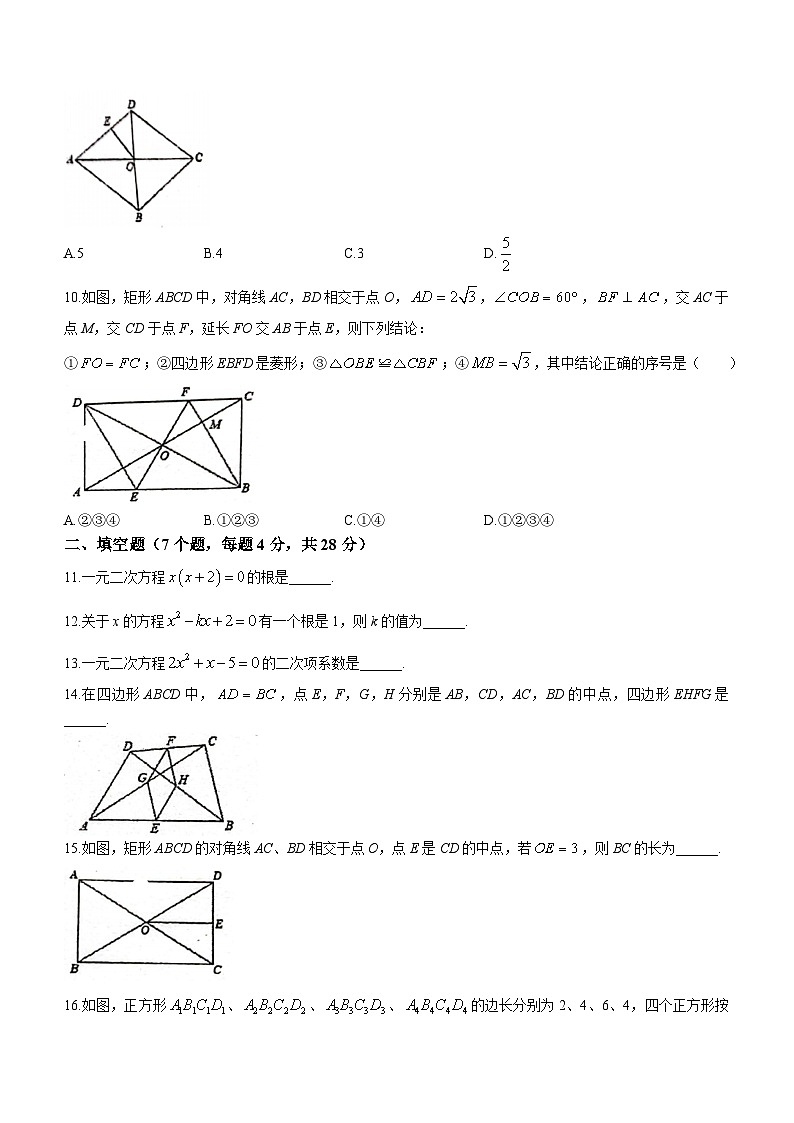
9.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点.若,,则OE的长为( )
A.5 B.4 C.3 D.
10.如图,矩形ABCD中,对角线AC,BD相交于点O,,,,交AC于点M,交CD于点F,延长FO交AB于点E,则下列结论:
①;②四边形EBFD是菱形;③;④,其中结论正确的序号是( )
A.②③④ B.①②③ C.①④ D.①②③④
二、填空题(7个题,每题4分,共28分)
11.一元二次方程的根是______.
12.关于x的方程有一个根是1,则k的值为______.
13.一元二次方程的二次项系数是______.
14.在四边形ABCD中,,点E,F,G,H分别是AB,CD,AC,BD的中点,四边形EHFG是______.
15.如图,矩形ABCD的对角线AC、BD相交于点O,点E是CD的中点,若,则BC的长为______.
16.如图,正方形、、、的边长分别为2、4、6、4,四个正方形按如图所示摆放,点,,分别位于正方形、、的对角线的交点,则重叠部分的阴影部分的面积之和是______.
17.将2021个形状、大小均相同的菱形按照如图所示的方式排成一列,使得右侧菱形的顶点与左侧菱形的对称中心重合、若这些菱形的边长为2,锐角为60,则阴影部分的面积总和等于______.
三、解答题(一)(3个题,每题6分,共18分)
18.解方程:
19.已知关于x的一元二次方程.
(1)当时,判断方程根的情况:
(2)设此方程的两个根分别为,,若,求m的值.
20.如图,菱形ABCD的对角线AC,BD交于点O,且,,连接EO.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若,求OE的长.
四、解答题(二)(3个题,每题8分,共24分)
21.如图,某中学准备建一个面积为的矩形花园,它的一边利用图书馆的后墙,另外三边所围的栅栏的总长度是40m,求垂直于墙的边AB的长度?(后墙MN最长可利用25米)
22.如图,在中,
(1)用尺规作图法作出的角平分线CD,交AB于点D;
(2)在(1)的条件下,若,,垂足分别为E、F,判断四边形CEDF的形状,并说明理由.
23.欣欣服装店经销某种品牌的童装,进价为50元/件,原来售价为100元/件,每天可以出售40件,经市场调查发现每降价1元,一天可以多售出2件.
(1)如果每天要获得2400元的利润,并使顾客得到更大的优惠,问每件应降价多少元?
(2)由于库存原因,经理决定降价销售,经过两次降价后每件童装的售价为81元/件,每次降价的百分率相同,求降价的百分率
五、解答题(三)(2个题,每题10分,共20分)
24.如图,在矩形ABCD中,,,动点P,Q分别从点A,C同时出发,点P以的速度向点B移动,一直到点B为止,点Q以的速度向点D移动(点P停止移动时,点Q也停止移动).设移动时间为,连接PQ,QB.
(1)当______时,P,Q两点间的距离为13cm.
(2)四边形APQD的形状可能为矩形吗?若可能,求出t的值;若不可能,请说明理由;
(3)当为等腰三角形时,求t的值;
25.综合与实践课上,老师让同学们以“正方形的折叠”为主题开展数学活动.
图1 图2 图3
(1)操作判断
操作:如图1,点E是边长为12的正方形纸片ABCD的边AD上一动点,将正方形沿着CE折叠,点D落在点F处,把纸片展平,射线DF交射线AB于点P.
判断:根据以上操作,图1中AP与EF的数量关系:______.
(2)迁移探究
在(1)条件下,若点E是AD的中点,如图2,延长CF交AB于点Q,点Q的位置是否确定?如果确定,求出线段BQ的长度,如果不确定,说明理由;
(3)拓展应用
在(1)条件下,如图3,CE,DF交于点G,取CG的中点H,连接BH,求BH的最小值.
43,广东省佛山市南海区桂城街道文翰中学2023-2024学年九年级上学期月考数学试题(无答案): 这是一份43,广东省佛山市南海区桂城街道文翰中学2023-2024学年九年级上学期月考数学试题(无答案),共6页。试卷主要包含了选择题,填空题,解答题一,解答题二,解答题三等内容,欢迎下载使用。
广东省佛山市南海区南海实验中学2023-2024学年九年级上学期月考数学试题: 这是一份广东省佛山市南海区南海实验中学2023-2024学年九年级上学期月考数学试题,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省佛山市南海区南海实验学校映月校区2023-2024学年八年级上学期第一次月考数学试题(无答案): 这是一份广东省佛山市南海区南海实验学校映月校区2023-2024学年八年级上学期第一次月考数学试题(无答案),共5页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












