专题4. 指对“六金花”与常见应用（备战2024高考数学-大一轮36个核心专题）

专题4.重要的指对组合型函数及其应用

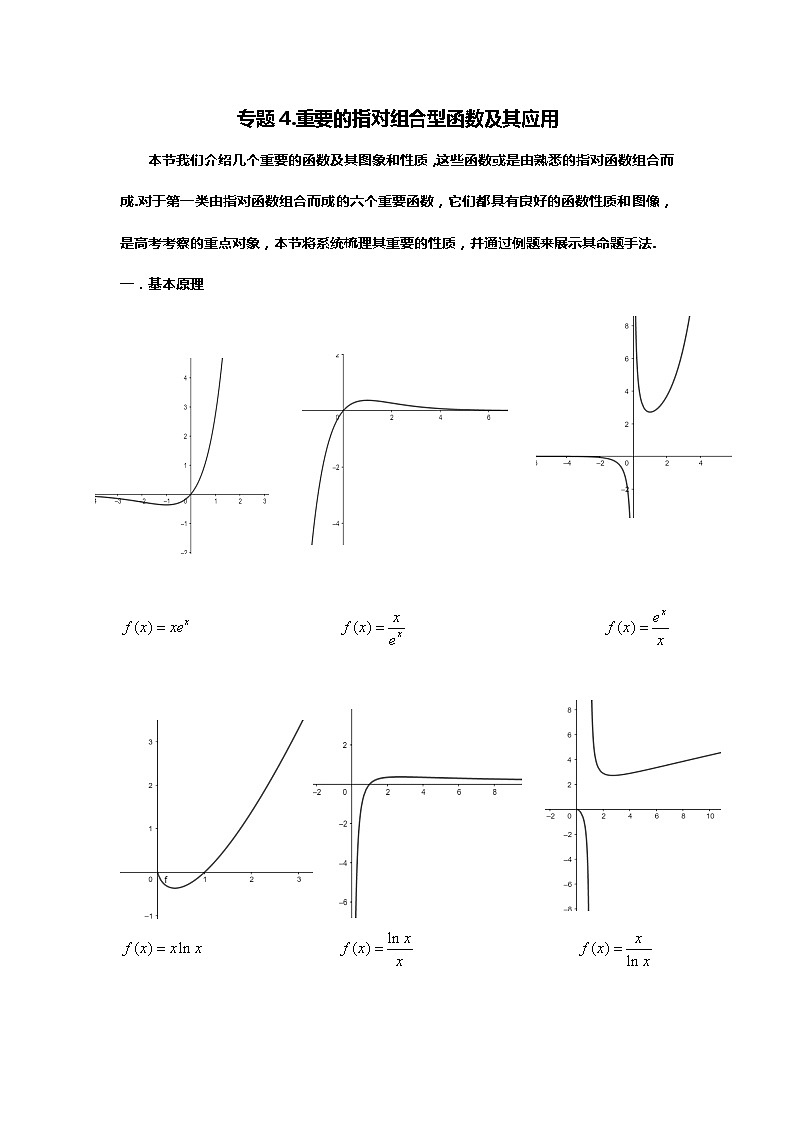
本节我们介绍几个重要的函数及其图象和性质，这些函数或是由熟悉的指对函数组合而成.对于第一类由指对函数组合而成的六个重要函数，它们都具有良好的函数性质和图像，是高考考察的重点对象，本节将系统梳理其重要的性质，并通过例题来展示其命题手法.

一．基本原理

上述六个指数或对数函数组合出的新函数及其图象是非常重要的.需要注意的是，对于函数与在处的极限值，需要由洛必达法则来计算，此处计算一个以展示其原理.

，故其图象在处趋近于.

除此之外，还需注意函数与函数的图象在正无穷远的特征，其它们图象都是上去了之后就不再下穿轴.

最后，要注意到与函数之间的基本关系，后者实际上是前者向上平移一个单位得到，在实际应用中，后者出现的频率也相当之高.

二．典例分析

1.考察函数基本性质.

例1．已知函数，若关于的方程有且仅有三个不同的实数解，则实数的取值范围是(    )

A． B． C． D．

解析：因为，所以，

当，；当，，

所以在和单调递减，在单调递增，

且当时，，，

故的大致图象如图所示：

关于的方程等价于，

即或，由图知，方程有且仅有一解，则有两解，

所以，解得，故选:C.

例2．已知函数关于的不等式只有一个整数解，则实数的取值范围是_____

解析：由，令，解得，

令，解得，的递增区间为，递减区间为，

故的最大值是，时，时，且，

故在时，，在时，，

①时，由不等式得或，

而时无整数解，的解集为，

整数解有无数多个，不合题意；

②时，由不等式得解集为，

整数解有无数多个，不合题意；

③时，由不等式，得或，

的解集为无整数解，只需的解集整数解只有一个，

且在上递增，在递减，而，这一正整数只能为3，，，综上所述，的取值范围是，故答案为.

2.朗博不等式.

朗博不等式是近年来随着函数同构出现的一个热门的不等式，其原理如下：下面主要注意的是，那么根据指数函数的基本不等式可得：

，

等号成立当且仅当.

例3．若，则实数的取值范围是（    ）

A． B． C． D．

解法1：因为，所以，设，则且原不等式可化为，只需．设，则，所以当时，，单调递减；当时，，单调递增．所以，所以．故选：B．

解法2：由不等式，可得.

例4.已知函数（，为自然对数的底数），.

（1）若有两个零点，求实数的取值范围；

（2）当时，对任意的恒成立，求实数的取值范围.

解析1.（2）当时，，原命题等价于对一切恒成立对一切恒成立.令  

，令，，则

在上单增，又，

，使即①当时，，当时，，即在递减，在递增，

由①知函数在单调递增即，实数的取值范围为.

解析2.由不等式，可得.

注意：朗博不等式命制的导数题目用通法解决时会出现同构型隐零点情形，即：

与这样的基本关系，读者在此处需特别注意.

3.凸凹反转

凸凹反转是证明不等式的一种技巧，欲证明，若可将不等式左端拆成，且的话，就可证明原不等式成立. 通常情况，我们一般选取为上凸型函数，为下凹型函数来完成证明.于是，这就需要我们熟悉高中阶段常见的六个具有这样特点的函数.关于上述六个函数的性质和图像的应用在之前已经讲过，本节主要的目标就是来展示凸凹反转技巧的基本应用手法和命题技术.

例如在上面六个函数中，我们可以选取凸函数，求导可得：，故可得在上减，上增，于是.

再考虑凹函数，则，故在处取得最大值，即

. 这样可得，即。

例5.设函数，曲线在点处的切线为．

（1）求；

（2）证明：．

解析：（2），从而等价于．设函数，

则，所以当时，；当时，．故在

上单调递减，在上单调递增，从而在上的最小值为．

设函数，则．所以当时，；当时，

．故在上单调递增，在上单调递减，从而在上的最大

值为.由于，所以当时，，即．

例6．设函数．

（1）当时，求的极值；

（2）当时，证明：在上恒成立．

解析：（2）当时，，下面证，即证，

设，则，在上，，是减函数；在上，

，是增函数．所以.

设，则，在上，，是增函数；在上，，

是减函数，所以.所以，即，所以

，即，即在上恒成立．

注：凸凹反转技巧性较强，是一种命题的好方法，但对于应试的考生而言，技巧性过强而难以掌握，同时，它的使用范围也比较局限.

4.指对同构

解决指对混合不等式时，常规的方法计算复杂，则将不等式变形为的结构，即为外层函数，其单调性易于研究.常见变形方式：①；②；③；④；⑤.

答题思路；

1.直接变形：

（1）积型：（同左）；

（同右）；

（取对数）.

说明：取对数是最快捷的，而且同构出的函数，其单调性一看便知.

（2）商型：（同左）；

（同右）；

（取对数）.

（3）和差型：（同左）；

（同右）.

2.先凑再变形：

若式子无法直接进行变形同构，往往需要凑常数、凑参数或凑变量，如两边同乘以，同加上等，再用上述方式变形.常见的有：

①；

②；

③

④

⑤

例7.（2022全国甲卷）

已知函数．

（1）若,求的取值范围；

（2）证明：若有两个零点，，则．

解析：（1），令，则，于是

.于是等价于在上恒成立，故.

（2）由（1）知要使得有两个零点，则

假设.要证明即证明，又由于在单增，即证明.下面构造函数

由于，又函数在单减，.

 时在单调递增，而

得证．

例8.已知函数．（为常数）若，若对任意的，恒成立，求实数的取值范围.

解析：由题意得：；

即：因为，当且仅当时等号成立，构造容易得：，所以只需要满足.

例9. 若，则（     ）

A.     B.  

 C.             D.

解析： A选项：，设

，设，则有恒成立，所以在单调递增，所以，从而存在，使得，由单调性可判断出：

，所以在不单调，不等式不会恒成立B选项：

，设可知单调递增.所以应该，B错误C选项：，构造函数，，则在恒成立。所以在单调递减，所以成立.

D选项：，同样构造，由C选项分析可知D错误.

例10．已知函数和有相同的最大值.

（1）求a；

（2）证明：存在直线y=b，其与两条曲线和共有三个不同的交点，并且从左到右的三个交点的横坐标成等比数列.

解析：（2）由（1）知，由于时，，时，，因此只有才可能满足题意，记，且，由（1）得在上单调递增，在单调递减，且，所以存在，使得，设，则，设，则，时，，递减，时，，递增，所以，所以，是增函数，时，，，又，所以存在，使得，即此时与有两个交点，其中一个交点在内，另一个交点在内，同理与也有两个交点，其中一个交点在内，另一个交点在内，若与和共有三个不同的交点，则其中一个交点为两条曲线和的公共点，记其横坐标为，令，则，记与的三个交点的横坐标从左到右依次为，且满足，且，即，又，且，且在和上分别单调，所以，即，所以为的等比中项，所以从左到右的三个交点的横坐标成等比数列.