云南省丽江市永胜县2020—2021学年上学期七年级期中数学试卷

这是一份云南省丽江市永胜县2020—2021学年上学期七年级期中数学试卷，共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年云南省丽江市永胜县七年级（上）期中数学试卷
一、单选题
1．下列式子：①a+b＝c；②；③a＞0；④a2n，其中属于代数式的是（　　）
A．①③ B．②④ C．①③④ D．①②③④
2．已知地球上海洋面积约为316 000 000km2，数据316 000 000用科学记数法可表示为（　　）
A．3.16×109 B．3.16×107 C．3.16×108 D．3.16×106
3．﹣4a2b的次数是（　　）
A．3 B．2 C．4 D．﹣4
4．给出下列判断：①在数轴上，原点两旁的两个点所表示的数都是互为相反数；②任何正数必定大于它的倒数，，都是整式；④x2﹣xy+y2是按字母y的升幂排列的多项式，其中判断正确的是（　　）
A．①② B．②③ C．③④ D．①④
5．﹣（+2）等于（　　）
A．﹣2 B．2 C．﹣ D．
6．下列各数中，互为相反数的是（　　）
A．+（﹣9）和﹣（+9） B．﹣（﹣9）和+（+9）
C．﹣（﹣9）和+（﹣9） D．﹣（﹣9）和﹣[+（﹣9）]
7．下面计算正确的是（　　）
A．6a﹣5a＝1 B．a+2a2＝3a2
C．﹣（a﹣b）＝﹣a+b D．2（a+b）＝2a+b
8．在排成每行七天的日历表中取下一个3×3方块（如图）．若所有日期数之和为189，则n的值为（　　）

A．21 B．11 C．15 D．9
9．已知a、b在数轴上的位置如图所示，那么下面结论正确的是（　　）

A．a+b＞0 B．a+b＞0（选项重复）
C．ab＜0 D．0
10．若|a|＝|b|，则a与b的关系是（　　）
A．a＝b B．a＝﹣b C．a＝b＝0 D．a＝b或a＝﹣b
二、填空题
11．（﹣）+＝　 　．
12．比较大小，用“＞”、“＜”、“＝”连接．（1）|﹣3|　 　﹣3；（2）　 　．
13．按括号内的要求，用四舍五入法求近似数：0.83284（精确到0.001）≈　 　．
14．如图是一个简单的数值运算程序，当输入x的值为﹣1时，则输出的结果应为　 　．
15．长方形的长为2b﹣a，宽比长少b，则这个长方形的周长是 　 　．
16．吉林广播电视塔“五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客　 　人（用含m、n的代数式表示）．
三、解答题
17．计算：
（1）﹣
（2）|﹣|+2．
18．合并同类项
（1）3x﹣y﹣2x+3y　      
（2）3a2b+2ab2+5﹣3a2b﹣5ab2﹣2．
19．先化简，再求值：2（x+2xy）﹣（3x+y）﹣4xy，y＝2．
20．把下列各数：﹣2.5，（﹣1）2，0，﹣|﹣2|，﹣（﹣3）在数轴上表示出来
21．某银行办储蓄业务：取出950元，存入500元，取出800元，取出1025元，存入2500元，请你计算一下，银行的现款增加了多少？
22．已知M＝4x2﹣2xy+y2，N＝x2﹣2xy+y2．
（1）化简：M﹣3N．
（2）当x＝﹣1，y＝2时．求M﹣3N+（﹣1）2023的值．
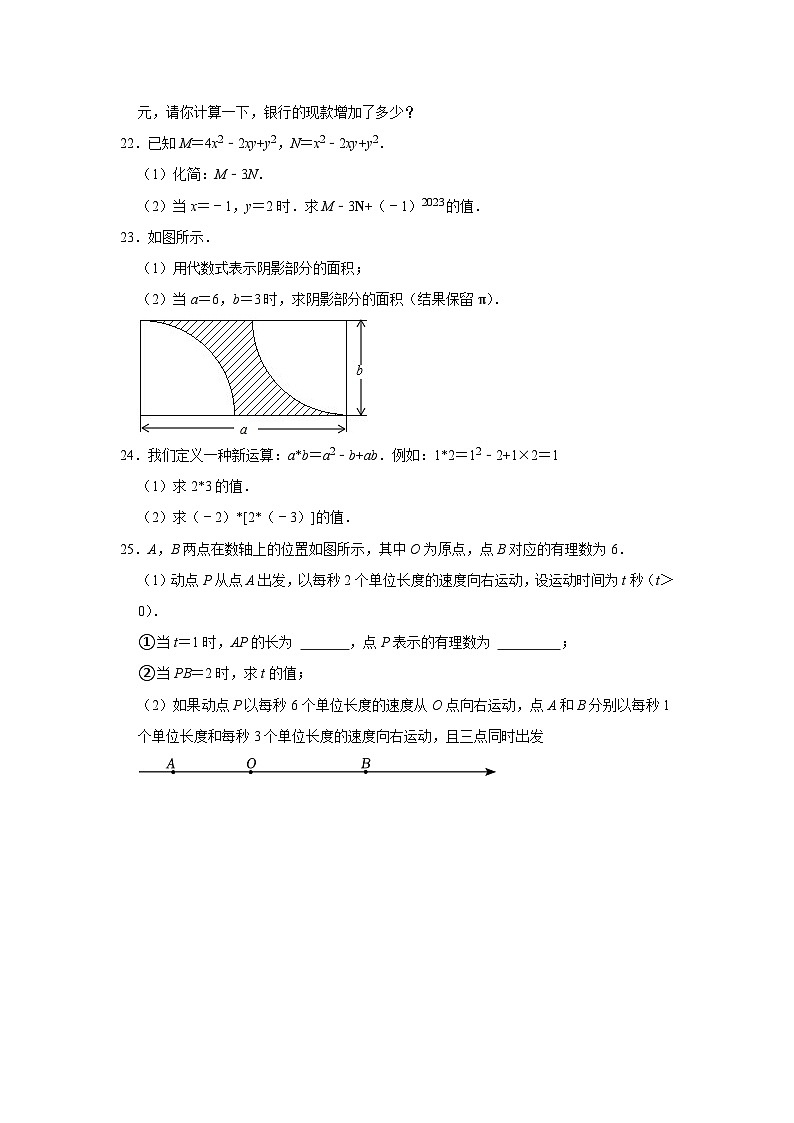
23．如图所示．
（1）用代数式表示阴影部分的面积；
（2）当a＝6，b＝3时，求阴影部分的面积（结果保留π）．

24．我们定义一种新运算：a*b＝a2﹣b+ab．例如：1*2＝12﹣2+1×2＝1
（1）求2*3的值．
（2）求（﹣2）*[2*（﹣3）]的值．
25．A，B两点在数轴上的位置如图所示，其中O为原点，点B对应的有理数为6．
（1）动点P从点A出发，以每秒2个单位长度的速度向右运动，设运动时间为t秒（t＞0）．
①当t＝1时，AP的长为 　 　，点P表示的有理数为 　 　；
②当PB＝2时，求t的值；
（2）如果动点P以每秒6个单位长度的速度从O点向右运动，点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动，且三点同时出发


2020-2021学年云南省丽江市永胜县七年级（上）期中数学试卷
参考答案与试题解析
一、单选题
1．下列式子：①a+b＝c；②；③a＞0；④a2n，其中属于代数式的是（　　）
A．①③ B．②④ C．①③④ D．①②③④
【分析】代数式是由数和字母组成，表示加、减、乘、除、乘方、开方等运算的式子，或含有字母的数学表达式，注意不能含有＝、＜、＞、≤、≥、≈、≠等符号．
【解答】解：①a+b＝c含有“＝”，所以不是代数式；
②是代数式；
③a＞6含有“＞”，所以不是代数式；
④a2n是代数式．
故选：B．
【点评】此题主要考查了代数式的定义，是基础题型．
2．已知地球上海洋面积约为316 000 000km2，数据316 000 000用科学记数法可表示为（　　）
A．3.16×109 B．3.16×107 C．3.16×108 D．3.16×106
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：316 000 8，
故选：C．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．﹣4a2b的次数是（　　）
A．3 B．2 C．4 D．﹣4
【分析】根据单项式次数的定义进行解答即可．
【解答】解：∵单项式﹣4a2b中所有字母指数的和＝7+1＝3，
∴此单项式的次数为2．
故选：A．
【点评】本题考查的是单项式次数的定义，即一个单项式中所有字母的指数的和叫做单项式的次数．
4．给出下列判断：①在数轴上，原点两旁的两个点所表示的数都是互为相反数；②任何正数必定大于它的倒数，，都是整式；④x2﹣xy+y2是按字母y的升幂排列的多项式，其中判断正确的是（　　）
A．①② B．②③ C．③④ D．①④
【分析】①根据数轴上数的特点解答；
②当一个正数大于0小于或等于1时，此解困不成立；
③根据整式的概念即可解答；
④根据升幂排列的定义解答即可．
【解答】解：①在数轴上，原点两旁的两个点所表示的数都是互为相反数，原点两旁的两个点如果到原点的距离相等；
②任何正数必定大于它的倒数，1的倒数还是1；
③7ab，，符合整式的定义都是整式；
④x2﹣xy+y2是按字母y的升幂排列的多项式，正确．
故选：C．
【点评】本题考查了相反数的概念，倒数的概念，整式的概念、多项式的排列，注意1的倒数还是1．
5．﹣（+2）等于（　　）
A．﹣2 B．2 C．﹣ D．
【分析】根据相反数的定义解答即可．
【解答】解：﹣（+2）＝﹣2，
故选：A．
【点评】此题考查相反数问题，关键是根据相反数的定义解答．
6．下列各数中，互为相反数的是（　　）
A．+（﹣9）和﹣（+9） B．﹣（﹣9）和+（+9）
C．﹣（﹣9）和+（﹣9） D．﹣（﹣9）和﹣[+（﹣9）]
【分析】根据相反数的定义，只有符号不同的两个数互为相反数，采用逐一检验法判断即可．
【解答】解：A、+（﹣9）＝﹣9，符号相同，
B、﹣（﹣2）＝9，符号相同，
C、﹣（﹣9）＝7，符号不同，
D、﹣（﹣9）＝9，符号相同，
故选：C．
【点评】本题考查了互为相反数的性质，只有符号不同的两个数互为相反数，难度适中．
7．下面计算正确的是（　　）
A．6a﹣5a＝1 B．a+2a2＝3a2
C．﹣（a﹣b）＝﹣a+b D．2（a+b）＝2a+b
【分析】直接利用去括号法则以及合并同类项法则分别化简求出即可．
【解答】解：A、6a﹣5a＝a；
B、a+5a2无法计算，故此选项错误；
C、﹣（a﹣b）＝﹣a+b；
D、2（a+b）＝7a+2b；
故选：C．
【点评】此题主要考查了去括号法则以及合并同类项，正确掌握运算法则是解题关键．
8．在排成每行七天的日历表中取下一个3×3方块（如图）．若所有日期数之和为189，则n的值为（　　）

A．21 B．11 C．15 D．9
【分析】观察图片，可以发现日历的排布规律，因此可得出日历每个方块的代数式，从而求出n的值．
【解答】解：日历的排布是有一定的规律的，在日历表中取下一个3×3方块，
当中间那个是n的话，它的上面的那个就是n﹣4，左边的那个就是n﹣1，左边最上面的那个就是n﹣1﹣6，右边最上面的那个就是n+1﹣7，若所有日期数之和为189，
则n+4+7+n+1﹣7+n﹣1+7+n﹣4﹣7+n+1+n﹣8+n+7+n﹣7+n＝189，
2n＝189，
解得：n＝21．
故选：A．
【点评】此题的关键是联系生活实际找出日历的规律，所以学生平时要养成爱观察爱动脑的习惯．
9．已知a、b在数轴上的位置如图所示，那么下面结论正确的是（　　）

A．a+b＞0 B．a+b＞0（选项重复）
C．ab＜0 D．0
【分析】先观察数轴，判断a，b的正负和绝对值的大小关系，然后根据有理数的加法法则判断A，B选项，再利用乘除法则判断C，D选项即可．
【解答】解：观察数轴可知：a＞0，b＜0，
∴a+b＜3，ab＜0，，
故A，B，D选项均不符合题意；
故选：C．
【点评】本题主要考查了有理数的加法和乘除运算，解题关键是根据数轴，判断a，b的正负和绝对值的大小关系．
10．若|a|＝|b|，则a与b的关系是（　　）
A．a＝b B．a＝﹣b C．a＝b＝0 D．a＝b或a＝﹣b
【分析】由|a|＝|b|，可知a与b可以相等或互为相反数，则可求得答案．
【解答】解：∵|a|＝|b|，
∴a＝±b，
即a＝b或a＝﹣b．
故选：D．
【点评】考查了绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．
二、填空题
11．（﹣）+＝　﹣　．
【分析】依据有理数的加法法则计算即可．
【解答】解；原式＝﹣（．
故答案为：﹣．
【点评】本题主要考查的是有理数的加法，掌握加法法则是解题的关键．
12．比较大小，用“＞”、“＜”、“＝”连接．（1）|﹣3|　＞　﹣3；（2）　＞　．
【分析】（1）先根据绝对值的性质计算绝对值，再比较大小．
（2）先通分，再根据两个负数比较大小的方法进行比较．
【解答】解：（1）∵|﹣3|＝3＞2，﹣3＜0；
（2）∵﹣＝﹣，﹣，|﹣|，
∴﹣＞﹣＞﹣．
【点评】有理数比较大小与实数比较大小相同：
（1）正数都大于0，负数都小于0，正数大于一切负数；
（2）两个负数，绝对值大的反而小．
13．按括号内的要求，用四舍五入法求近似数：0.83284（精确到0.001）≈　0.833　．
【分析】根据四舍五入法可以解答本题．
【解答】解：0.83284（精确到0.001）≈5.833，
故答案为：0.833．
【点评】本题考查近似数和有效数字，解答本题的关键是明确近似数和有效数字的含义．
14．如图是一个简单的数值运算程序，当输入x的值为﹣1时，则输出的结果应为　1　．
【分析】把x的值代入数值运算程序中计算即可得到输出结果．
【解答】解：把x＝﹣1代入数值运算程序得：
[（﹣1）5﹣（﹣1）]÷2
＝（3+1）÷2
＝6÷2
＝1．
故答案为：8．
【点评】此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
15．长方形的长为2b﹣a，宽比长少b，则这个长方形的周长是 　6b﹣4a　．
【分析】根据题意表示出宽，即可求出周长．
【解答】解：根据题意得：2[（2b﹣a）+（b﹣a）]＝3（3b﹣2a）＝4b﹣4a．
故答案为：6b﹣5a．
【点评】此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
16．吉林广播电视塔“五一”假期第一天接待游客m人，第二天接待游客n人，则这2天平均每天接待游客　　人（用含m、n的代数式表示）．
【分析】用两天接待的游客总人数除以天数，即可得解．
【解答】解：2天平均每天接待游客．
故答案为：．
【点评】本题考查了列代数式，比较简单，熟练掌握平均数的求法是解题的关键．
三、解答题
17．计算：
（1）﹣
（2）|﹣|+2．
【分析】（1）先算立方根、算术平方根，再相减即可求解；
（2）先算绝对值，再合并同类项即可求解．
【解答】解：（1）﹣
＝﹣8﹣9
＝﹣11；
（2）|﹣|+2
＝﹣++2
＝+．
【点评】本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握立方根、算术平方根、绝对值、合并同类项等考点的运算．
18．合并同类项
（1）3x﹣y﹣2x+3y　      
（2）3a2b+2ab2+5﹣3a2b﹣5ab2﹣2．
【分析】（1）根据合并同类项的法则，合并整式中的同类项即可；
（2）根据合并同类项的法则，直接合并整式中的同类项即可．
【解答】解：（1）原式＝x+2y；
（2）原式＝﹣3ab4+3．
【点评】本题考查合并同类项的知识，要求掌握同类项的概念，会辨别同类项，并准确地掌握判断同类项的两条标准：带有相同系数的代数项；字母和字母指数．
19．先化简，再求值：2（x+2xy）﹣（3x+y）﹣4xy，y＝2．
【分析】先利用乘法分配律将2（x+2xy）算出来，然后经过去括号，合并同类项化简即可；最后再将x，y值分别代入计算结果．
【解答】解：2（x+2xy）﹣（3x+y）﹣4xy
＝2x+3xy﹣3x﹣y﹣4xy
＝﹣x﹣y，
当x＝﹣3，y＝2时．
【点评】本题考查了整式的加减运算，以及求代数式的值；熟记整式的加减运算法则是解题关键．
20．把下列各数：﹣2.5，（﹣1）2，0，﹣|﹣2|，﹣（﹣3）在数轴上表示出来
【分析】先把各数在数轴上表示出来，从左到右用“＜”连接起来即可．
【解答】解：如图所示，
，
故﹣2.5＜﹣|﹣5|＜0＜（﹣1）5＜﹣（﹣3）．
【点评】本题考查的是有理数的大小比较，熟知数轴上右边的数总比左边的大的特点是解答此题的关键．
21．某银行办储蓄业务：取出950元，存入500元，取出800元，取出1025元，存入2500元，请你计算一下，银行的现款增加了多少？
【分析】首先记取出为负，存入为正，即可得银行的现款增加了：﹣950+500﹣800+1200﹣1025+2500﹣200，继而求得答案．
【解答】解：﹣950+500﹣800+1200﹣1025+2500﹣20＝1405（元）．
答：银行的现款增加了1405元．
【点评】此题考查了有理数的加减混合运算．此题难度不大，注意理解正数与负数的意义．
22．已知M＝4x2﹣2xy+y2，N＝x2﹣2xy+y2．
（1）化简：M﹣3N．
（2）当x＝﹣1，y＝2时．求M﹣3N+（﹣1）2023的值．
【分析】（1）直接利用整式的加减运算法则计算得出答案；
（2）把x，y的值代入求出答案．
【解答】解：（1）解：M﹣3N＝（4x3﹣2xy+y2）﹣6（x2﹣2xy+y6）
＝4x2﹣3xy+y2﹣3x4+6xy﹣3y8
＝x2+4xy﹣7y2．
（2）当x＝﹣1，y＝2时，
原式＝（﹣1）2+3×（﹣1）×2﹣8×22﹣7
＝1﹣8﹣2﹣1
＝﹣16．
【点评】本题主要考查了整式的加减运算，正确合并同类项是解题的关键．
23．如图所示．
（1）用代数式表示阴影部分的面积；
（2）当a＝6，b＝3时，求阴影部分的面积（结果保留π）．

【分析】（1）根据阴影部分的面积等于长方形的面积减去两个扇形面积，分别表示出来即可，
（2）把a＝6，b＝3代入代数式，按照代数式规定的运算进行计算即可．
【解答】解：（1）
（2）当a＝6，b＝3时，
S＝
【点评】考查列代数式，代数式求值，根据具体的数量关系或图形中存在的某种关系，用字母和及运算表示，是正确解答的关键．
24．我们定义一种新运算：a*b＝a2﹣b+ab．例如：1*2＝12﹣2+1×2＝1
（1）求2*3的值．
（2）求（﹣2）*[2*（﹣3）]的值．
【分析】（1）利用新运算的定义解答即可；
（2）利用新运算的定义先算中括号后再利用新运算的定义运算即可．
【解答】解：（1）原式＝22﹣2+2×3
＝5﹣3+6
＝7+6
＝7；
（2）原式＝（﹣7）*[22﹣（﹣3）+2×（﹣3）]
＝（﹣4）*[4+3﹣6]
＝（﹣2）*1
＝（﹣7）2﹣1+（﹣8）×1
＝4﹣3﹣2
＝1．
【点评】本题主要考查了有理数的混合运算，本题是新定义型，理解并熟练应用新运算的定义解答是解题的关键．
25．A，B两点在数轴上的位置如图所示，其中O为原点，点B对应的有理数为6．
（1）动点P从点A出发，以每秒2个单位长度的速度向右运动，设运动时间为t秒（t＞0）．
①当t＝1时，AP的长为 　2　，点P表示的有理数为 　﹣2　；
②当PB＝2时，求t的值；
（2）如果动点P以每秒6个单位长度的速度从O点向右运动，点A和B分别以每秒1个单位长度和每秒3个单位长度的速度向右运动，且三点同时出发

【分析】（1）①根据路程＝速度×时间，以及线段的和差定义计算即可；
②分两种情形分别求解即可；
（2）分两种情形分别构建方程即可解决问题；
【解答】解：（1）①∵动点P从点A出发，以每秒2个单位长度的速度向右运动，
∴当t＝1时，AP＝3，
∵OA＝4，
∴OP＝2，
∴点P表示的有理数为﹣2．
故答案为2，﹣2；

②当点P在B左侧时，∵AB＝10，
∴AP＝2，
∴t＝4．
当点P在点B右侧时，AP＝12，
∴t＝6；

（2）设一点时间为t秒；
①当P在A、B之间时，PB＝3+3t﹣6t＝5﹣3t，
∵PA＝2PB，
∴5+5t＝2（7﹣3t），
解得t＝．
②当P点在B点右侧时，PA＝6+5t，
∵PA＝2PB，
∴6+5t＝2（7t﹣6），
解得t＝16，
故经过秒或16秒时．
【点评】本题考查实数与数轴、路程、速度、时间之间的关系等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/10/8 16:10:04；用户：娄老师；邮箱：15225657626；学号：48669677