精品解析：2022年广东省深圳市福田区13校联考九年级数学试题

2022年广东省深圳市福田区九年级数学13校联考试题

一．选择题（本题有10小题，每小题3分，共30分，在每小题给出的选项中，只一项是符合题目要求的，请将正确的选项用铅笔涂在答题卡上．）

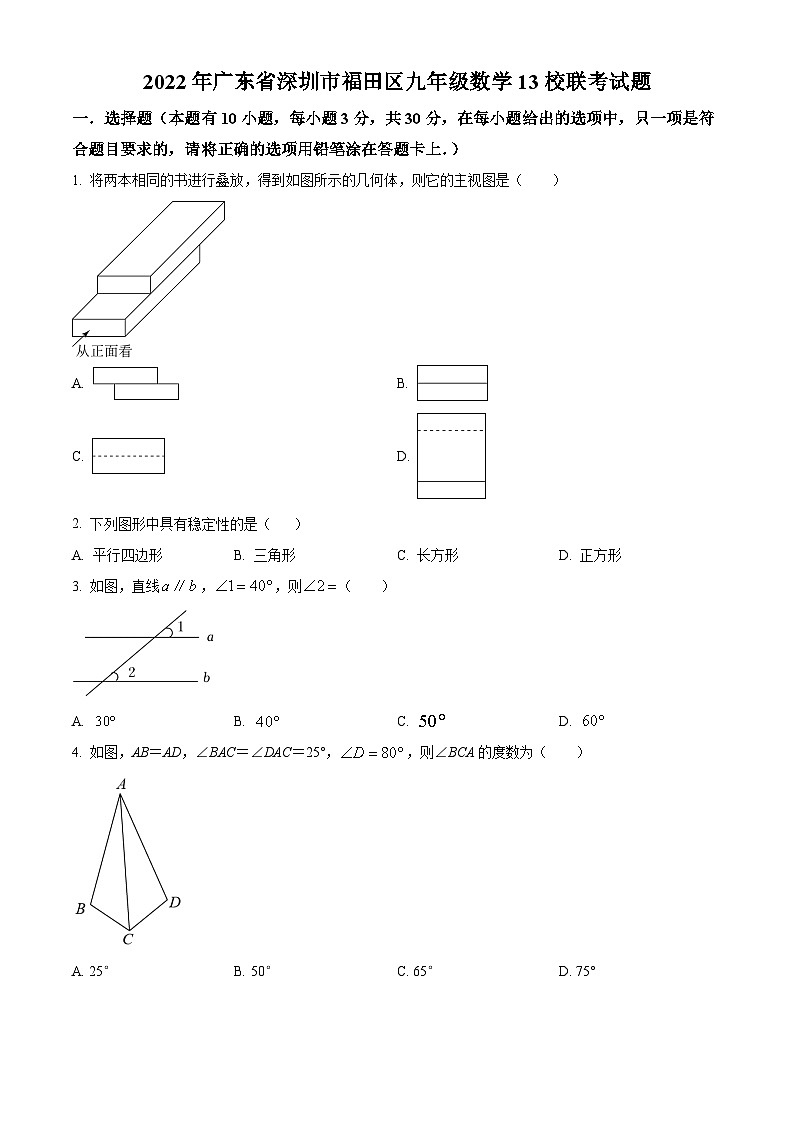
1. 将两本相同的书进行叠放，得到如图所示的几何体，则它的主视图是（　　）

A.  B.

C.  D.

【答案】B

【解析】

【分析】根据从正面看得到的图形是主视图，即可得到答案．

【详解】解：从正面看，看到的图形是由两个一样的长方形上下叠放组成的长方形，即看到的图形为，

故选B．

【点睛】本题考查了简单组合体的三视图，熟知三视图的定义是解题的关键．

2. 下列图形中具有稳定性的是（    ）

A. 平行四边形 B. 三角形 C. 长方形 D. 正方形

【答案】B

【解析】

【分析】根据三角形具有稳定性，四边形具有不稳定性可得结论．

【详解】解：三角形具有稳定性；

故选：B．

【点睛】本题考查了三角形的稳定性和四边形的不稳定性，比较简单．

3. 如图，直线，，则（　　）

A.  B.  C.  D.

【答案】B

【解析】

【分析】根据两直线平行，同位角相等，即可求解．

【详解】解：∵，

∴．

故选：B．

【点睛】此题考查了平行线的性质，解题的关键是熟练掌握平行线的有关性质．

4. 如图，AB＝AD，∠BAC＝∠DAC＝25°，，则∠BCA的度数为（　　）

A 25° B. 50° C. 65° D. 75°

【答案】D

【解析】

【分析】根据证明，可得，根据三角形内角和定理即可求得的度数．

【详解】解：与中，

，

，

，

．

故选D．

【点睛】本题考查了全等三角形的判定以及性质，三角形内角和定理，熟练掌握全等三角形的性质与判定是解题的关键．

5. 已知，则=（   ）

A.  B.  C.  D. 17

【答案】A

【解析】

【分析】根据比例的性质，由，得，则设，得到，，然后把，，代入中进行分式的运算即可．

【详解】解：∵，

∴，

设，得到，，

∴，

故选：A．

【点睛】本题考查了比例的性质：常用的性质有内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．

6. 同时抛掷两枚质地均匀的硬币，则一枚硬币正面向上､一枚硬币反面向上的概率是（    ）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据题意可画出树状图，然后进行求解概率即可排除选项．

【详解】解：由题意得：

∴一枚硬币正面向上､一枚硬币反面向上的概率是；

故选C．

【点睛】本题主要考查概率，熟练掌握利用树状图求解概率是解题的关键．

7. 在平面直角坐标系中，将一次函数（k是常数）图象向上平移2个单位长度后经过点，则k的值为（　　）

A. 1 B.  C.  D. 2

【答案】A

【解析】

【分析】先求出平移后的直线解析式，再根据平移后的直线经过点即可利用待定系数法求出答案．

【详解】解：由题意得，平移后的一次函数解析式为，

∵平移后的直线经过点，

∴，

∴，

故选A．

【点睛】本题主要考查了一次函数图象的平移，求一次函数解析式，正确求出平移后的一次函数解析式是解题的关键．

8. 如图，四边形是的内接四边形，连接、，若，则的度数是（　　）

A.  B.  C.  D.

【答案】C

【解析】

【分析】根据圆周角定理求出，根据圆内接四边形的性质计算，得到答案．

【详解】解：∵，

∴，

∵四边形是的内接四边形，

∴，

故选C．

【点睛】本题考查的是圆内接四边形的性质、圆周角定理，掌握圆内接四边形的对角互补是解题的关键．

9. 已知抛物线（a，b，c均为常数，）的顶点是，且该抛物线经过点，，若，则的取值范围是（　　）

A.  B.  C.  D. 且

【答案】D

【解析】

【分析】根据可知抛物线开口向上，离对称轴越远函数值越大，由此可知对称轴在和4之间，且离更近或对称轴在4的右边，据此求解即可．

【详解】解：∵抛物线（a，b，c均为常数，）的顶点是，且经过点，，，

∴抛物线开口向上，

∴离对称轴越远函数值越大，在对称轴左侧y随x增大而减小，在对称轴右侧y随x增大而增大，

∴或，

∴且，

故选D．

【点睛】本题主要考查了二次函数图象的性质，正确得到抛物线开口向上，离对称轴越远函数值越大是解题的关键．

10. 如图①，在▱ABCD中，动点P从点B出发，沿折线B→C→D→B运动，设点P经过的路程为x，△ABP的面积为y，y是x的函数，函数的图象如图②所示，则图②中的a值为（　　）

A. 3 B. 4 C. 14 D. 18

【答案】A

【解析】

【分析】由图②知，BC=6，CD=14-6=8，BD=18-14=4，再通过解直角三角形，求出△CBD高，进而求解．

【详解】解：由图②知，BC=6，CD=14-6=8，BD=18-14=4，

过点B作BH⊥DC于点H，

设CH=x，则DH=8-x，

则BH2=BC2-CH2=BD2-DH2，即：BH2=42-（8-x）2=62-x2，

解得：

则：，

则，

故选：A．

【点睛】本题考查的是动点图象问题，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．

二、填空题（本题有5小题，每小题3分，共15分．把答案填在答题卡上）

11. 分解因式：=_______．

【答案】4（x+2）（x-2）

【解析】

【分析】先提公因式4，然后使用平方差公式因式分解即可．

【详解】解：原式=4（x2-4）

=4（x+2）（x-2）．

【点睛】本题考查了提公因式法和公式法，熟练掌握平方差公式a2-b2=（a+b）（a-b）是解题的关键．

12. 函数y＝中自变量x的取值范围是________

【答案】

【解析】

【分析】二次根式有意义的条件：二次根号内的数为非负数，二次根式才有意义.

【详解】由题意得，1−2x≥0，

解得： x≤.

故答案为：x≤.

【点睛】本题考查二次根式有意义的条件，本题属于基础应用题，只需学生熟练掌握二次根式有意义的条件，即可完成.

13. 人字梯为现代家庭常用的工具．如图，若，的长都为，当时，人字梯顶端离地面的高度为__________．（参考数据：，，）

【答案】2.05

【解析】

【分析】在Rt△ADC中，求出AD即可．

【详解】解：∵AB=AC=2.5m，AD⊥BC，

∴∠ADC=90°，

∴AD=AC•sin55°=2.5×0.82≈2.05（m），

故答案为2.05．

【点睛】本题考查解直角三角形的应用，解题的关键是理解题意，灵活运用所学知识解决问题．

14. 已知实数、满足，若关于的一元二次方程的两个实数根分别为，则的值为___

【答案】1

【解析】

【分析】根据非负数的性质得出a=2，b=-3，根据根与系数的关系可得，，整体代入即可求得．

【详解】解：，

，，

，，

关于的一元二次方程的两个实数根分别为，

，，

，

故答案为：1．

【点睛】本题考查了非负数性质以及一元二次方程的根与系数的关系，解决本题的关键是熟练掌握一元二次方程根与系数的关系．

15. 如图，在矩形中，，，点N是边上的中点，点M是边上的一动点连接，将沿折叠，若点B的对应点，连接，当为直角三角形时，的长为 _____．

【答案】或5

【解析】

【分析】分情况讨论：当时，当时，当时，再分别利用勾股定理和翻折的性质可得答案；

【详解】解：∵为直角三角形，

当时，

∵点N是边上的中点，，

∴，

∵，

∴点B的对应点不能落在所在直线上，

∴，不存在此类情况；

当时，如图所示，

由折叠性质可得，

，

∴；

当时，如图所示

∵，

∴、N、C三点共线，

由勾股定理可得，

，

设，则，

∴，

解得：，

综上所述的长为或5．

【点睛】本题考查翻折的性质，根据题意画出图形并分情况讨论是解题关键．

二、解答题（7小题，共55分）

16. 解方程

（1）；

（2）

【答案】（1），   

（2），

【解析】

【分析】（1）先移项得到，利用因式分解法把方程转化为或，然后解两个一次方程即可．

（2）原方程运用配方法求解即可．

【小问1详解】

，

，

，

或，

∴，

【小问2详解】

∴，

【点睛】本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．也考查了用配方法解一元二次方程．

17. 先化简，再求值，其中．

【答案】

【解析】

【分析】首先对括号内的式子进行通分相加，把除法转化为乘法，进行约分，最后代入数值计算即可．

【详解】原式，

 当 时，原式

【点睛】本题考查了分式的混合运算以及化简求值，熟练掌握因式分解，通分约分是解题的关键．

18. 北京2022年冬奥会的成功举办，激起了同学们对冰雪运动的广泛兴趣．某校对部分学生进行了“我最喜欢的冰雪运动项目”的问卷调查，要求参加问卷调查的学生在冰球、冰壶、短道速滑、高山滑雪四项冰雪运动项目中选且只选一项．根据调查结果，绘制了如下两幅不完整的统计图．根据图中信息，解答下列问题：

（1）求参加这次调查的学生总人数和选择“冰壶”的学生人数；

（2）求扇形统计图中“高山滑雪”对应扇形的圆心角度数；

（3）该校共有1200名学生，请你估算其中最喜欢“短道速滑”的学生人数．

【答案】（1）参加这次调查的学生总人数为40人，选择“冰壶”的人数为12人   

（2）扇形统计图中“高山滑雪”对应的扇形的圆心角度数是36°   

（3）该校共有1200名学生，估算其中最喜欢“短道速滑”的学生人数为540人

【解析】

【分析】（1）用最喜欢冰球的学生人数除以所占的百分比即可得出抽取的总人数，再根据喜欢冰壶的学生所占的百分比可得喜欢冰壶的学生人数；
（2）先算出喜欢“高山滑雪”的人数所占的百分比，再用360°乘百分比可得圆心角；
（3）用总人数乘以最喜欢短道速滑的学生所占的百分比，即可得出答案．

【小问1详解】

学生总人数（人）

选择“冰壶”的人数（人）

故参加这次调查的学生总人数为40人，选择“冰壶”的人数为12人；

【小问2详解】

“高山滑雪”对应扇形的圆心角度数

故扇形统计图中“高山滑雪”对应的扇形的圆心角度数是36°；

【小问3详解】

最喜欢“短道速滑”的学生人数（人）

故该校共有1200名学生，估算其中最喜欢“短道速滑”的学生人数为540人．

【点睛】本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．

19. 如图，四边形ABCD内接于⊙O，AB为⊙O的直径，对角线AC，BD交于点E，⊙O的切线AF交BD的延长线于点F，且AE=AF．

（1）求证：BD平分∠ABC；

（2）若AF=3，BF=5，求BE的长．

【答案】（1）证明过程见详解   

（2）

【解析】

【分析】（1）先证△AED≌△AFD，得到∠DAE=∠DAF，DE=DF，根据圆周角定理可得∠DBC=∠DAC=∠DAF，再根据切线的性质证明∠FAD=∠ABD，即可得证；

（2）证明△BFA∽△AFD，即有，即可求出DF，结合DE=DF即可求出BE．

【小问1详解】

∵AB是⊙O的直径，

∴∠ADB=90°，

∴∠ADF=∠ADB=90°，

∴∠F+∠FAD=90°，

∵AE=AF，

∴∠AEF=∠AFE，

∴△AED≌△AFD，

∴∠DAE=∠DAF，DE=DF，

∴∠DBC=∠DAC=∠DAF，

∵AF是⊙O的切线，

∴∠FAB=90°，

∴∠F+∠ABD=90°，

∵∠F+∠FAD=90°，

∴∠FAD=∠ABD，

∵∠DBC=∠FAD，

∴∠DBC=∠ABD，

∴BD平分∠ABC；

【小问2详解】

∵∠FAD=∠ABD，∠F=∠F，

∴△BFA∽△AFD，

∴，

∵BF=5，AF=3，

即，

在（1）中已证得DE=DF，

∴BE=BF-DE-DF=5-=．

【点睛】本题考查了切线的性质、圆周角定理、角平分线的判定、全等三角形的判定与性质、相似三角形的判定与性质等知识，灵活利用圆周角定理是解答本题的关键．

20. 为支持国家南水北调工程建设，小王家由原来养殖户变为种植户，经市场调查得知，当种植樱桃的面积x不超过15亩时，每亩可获得利润y＝1900元；超过15亩时，每亩获得利润y（元）与种植面积x（亩）之间的函数关系如下表（为所学过的一次函数，反比例函数或二次函数中的一种）

（1）请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式；

（2）如果小王家计划承包荒山种植樱桃，受条件限制种植樱桃面积x不超过50亩，设小王家种植x亩樱桃所获得的总利润为W元，求小王家承包多少亩荒山获得的总利润最大，并求总利润W（元）的最大值．

【答案】（1）；（2）小王家承包50亩荒山获得的总利润最大，总利润的最大值为60000元

【解析】

【分析】（1）根据题意设y＝kx＋b，利用待定系数法求解可得；

（2）根据总利润＝每亩利润×亩数，分0＜x≤15和15＜x≤50两种情况，分别利用一次函数和二次函数的性质求解可得．

【详解】解：（1）由题意，设，

将，和，代入得：，

解得：，

，

验证：当时，；当时，，符合题意，

故y与x的函数关系式为：；

（2）由题意得：当时，，

此时当时，最大元；

当时，，

∵－20＜0，且x≤50，

∴当时，最大元，

综上，小王家承包50亩荒山获得的总利润最大，总利润的最大值为60000元．

【点睛】本题主要考查一次函数和二次函数的实际应用，熟练掌握待定系数法，正确列出函数解析式是解题的关键．

21. 如图1，已知抛物线y=ax2+bx+c（a≠0）与x轴交于A（-1，0）、B（4，0）两点，与y轴交于点C（0，2），点P是抛物线上的一个动点，过点P作PQ⊥x轴，垂足为Q，交直线BC于点D．

（1）求该抛物线的函数表达式；

（2）若以P、D、O、C为顶点的四边形是平行四边形，求点Q的坐标；

（3）如图2，当点P位于直线BC上方的抛物线上时，过点P作PE⊥BC于点E，设△PDE的面积为S，求当S取得最大值时点P的坐标，并求S的最大值．

【答案】（1）y=-x2+x+2；（2）Q点坐标为（2，0）或（2+2，0）或（2-2，0）；（3）当P为（2，3）时，S有最大值，最大值为=．

【解析】

【分析】（1）把A、B、C三点的坐标代入可求得a、b、c的值，可得出函数表达式；

（2）可先求得BC的解析式，设出Q点坐标，可表示出D点坐标和P点坐标，可表示出PD的长，由条件可得PD=OC=2，可求得P点坐标，则可得Q点的坐标；

（3）可设出P的坐标，由PQ∥OC可表示出DQ、BD，由△PED∽△BQD可表示出PE和DE，则可表示出S，再结合P在直线BC上方，可求得S的最大值，可求得P点的坐标．

【详解】（1）∵二次函数与x轴交于A（-1，0）、B（4，0）两点，与y轴交于点C（0，2），

∴代入二次函数解析式可得，得    ，

∴二次函数表达式为y=-x2+x+2；

（2）设直线BC解析式为y=kx+b，

∵B（4，0），C（0，2），

∴代入可得，

解得，

∴直线BC解析式为y=-x+2，

设Q坐标为（m，0），则可知D点坐标为（m，-m+2），

又∵P点在抛物线上，

∴P点坐标为（m，-m2+m+2），

当P、D、O、C为顶点的四边形为平行四边形时，则有PD=OC=2，

即|-m2+m+2-（-m+2）|=2，即|-m2+2m|=2，

当-m2+2m=2时，解得m=2，则Q坐标为（2，0），

当-m2+2m=-2时，解得m=2±2，则Q坐标为（2+，0）或（2-，0），

综上可知Q点坐标为（2，0）或（2+2，0）或（2-2，0）；

（3）设Q点坐标为（n，0），由（2）可知D为（n，-n+2），P点坐标为（n，-n2+n+2），

∴PD=-n2+2n=n（4-n），DQ=-n+2，

又∵OB=4，

∴BQ=4-n，

在Rt△OBC中，OC=2，OB=4，由勾股定理可求得BC=2，

∵OQ∥OC，

∴，即，解得BD=，

∵PE⊥BC，PQ⊥QB，

∴∠PED=∠BQD=90°，且∠PDE=∠BDQ，

∴△PED∽△BQD，

∴，

即，

解得PE=，DE=，

∴S=PE•DE=××=（-n2+4n）2，

令t=-n2+4n=-（n-2）2+4，

∵P在直线BC上方，

∴0＜n＜4，

∴0＜t≤4，且当n=2时，t有最大值4，

此时P点坐标为（2，3），

∴当t=4时，Smax=×42=，

综上可知当P（2，3）时，S有最大值，最大值为=．

【点睛】本题主要考查待定系数法求函数解析式及平行四边形的性质、平行线分线段成比例和相似三角形的判定和性质．在（1）中注意待定系数法应用的关键是点的坐标，在（2）中用Q的坐标表示出PD的长度，得到关于Q点坐标的方程是解题的关键，在（3）中用Q点的坐标表示出PE、DE的长度是解题的关键．本题知识点多，计算量大，难度较大．

.

22. 问题背景：如图（1），△ABD，△AEC都是等边三角形，△ACD可以由△AEB通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．

尝试应用：如图（2），在Rt△ABC中，∠ACB＝90°，分别以AC，AB为边，作等边△ACD和等边△ABE，连接ED，并延长交BC于点F，连接BD．若BD⊥BC，求DF：DE的值．

拓展创新：如图（3），在Rt△ABC中，∠ACB＝90°，AB＝2，将线段AC绕点A顺时针旋转90°得到线段AP，连接PB，直接写出PB的最大值．

【答案】（1）旋转中心是点A，旋转方向是顺时针，旋转角是；（2）；（3）+1

【解析】

【分析】（1）由等边三角形得出，，，，证明，由旋转性质即可得出答案；

（2）证明，由全等三角形的性质得，，得出，由直角三角形性质得，则可计算出答案；

（3）过点A作，且使AE=AD，连接PE，BE，由直角三角形的性质求出BE、PE的长即可得解．

【详解】解：（1）∵，都是等边三角形，

∴，，，，，

，

，

可以由绕点A顺时针旋转得到，

即旋转中心是点A，旋转方向是顺时针，旋转角是；

（2）和都是等边三角形，

，，，

，

，

，，

，

，

，

，

，

，

，

设BF=x，则CF=DF=2x，DE=3x，

∴；

（3），

∴ 点C在以AB为直径的圆上运动，取AB的中点D，连接CD，

，

如图，过点A作，且使AE=AD，连接PE，BE，

∵ 将线段AC绕点A顺时针旋转得到线段AP，

，PA=AC．

，

，

，

∴ PE=CD=1．

∵ AB=2，AE=AD=1，

∴ BE===，

，

∴ BP的最大值为+1．

【点睛】本题是几何变换综合题，考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理、直角三角形的性质、圆周角定理；熟练掌握旋转的性质是解题关键．