第十一章 三角形 章末检测卷-八年级数学上册高频考点专题突破（人教版）

第十一章  三角形章末检测卷（人教版）

姓名：__________________     班级：______________   得分：_________________

注意事项：

本试卷满分120分，考试时间90分钟，试题共26题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．

一、选择题（本大题共12小题，每小题3分，共36分）在每小题所给出的四个选项中，只有一项是符合题目要求的．

1．（2021·山东滨州市·八年级期末）三角形按边分类可以用集合来表示，如图所示，图中小椭圆圈里的A表示（　　）

A．直角三角形 B．锐角三角形 C．钝角三角形 D．等边三角形

2．（2021·贵州铜仁市·中考真题）用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌．工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌（      ）

A．等边三角形 B．正方形 C．正五边形 D．正六边形

3．（2020·浙江八年级期末）如图，在中，的延长线于点D，的长线于点E．于点C，延长线于点E，于点C，下列说法错误的是（    ）

A．是的AB边上的高 B．是的边上的高

C．是的边上的高 D．不是的高

4．（2021·深圳市龙岗区百合外国语学校八年级期中）下列叙述正确的是（    ）

①三角形的中线、角平分线都是射线；②三角形的中线将三角形分成面积相等的两个小三角形；③三角形的三条高交于一点；④三角形的三条角平分线交于一点．

A．②④ B．①②④ C．③④ D．④

5．（2020·浙江八年级期末）如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2、3、4、6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任意两个螺丝间的距离的最大值为（    ）

A．6 B．7 C．8 D．10

6．（2021·江苏八年级期中）将一副直角三角板按如图放置（其中），使含角的三角板的较长直角边与等腰直角三角板的斜边平行，则图中的度数为（    ）

A． B． C． D．

7．（2021·湖北蔡甸初二期中）如图，若的三条角平分线、、交于点，则与互余的角是(      )

A． B． C． D．

8．（2021·江苏镇江市·八年级期中）已知中，是边上的高，平分．若，，，则的度数等于（    ）

A． B． C． D．

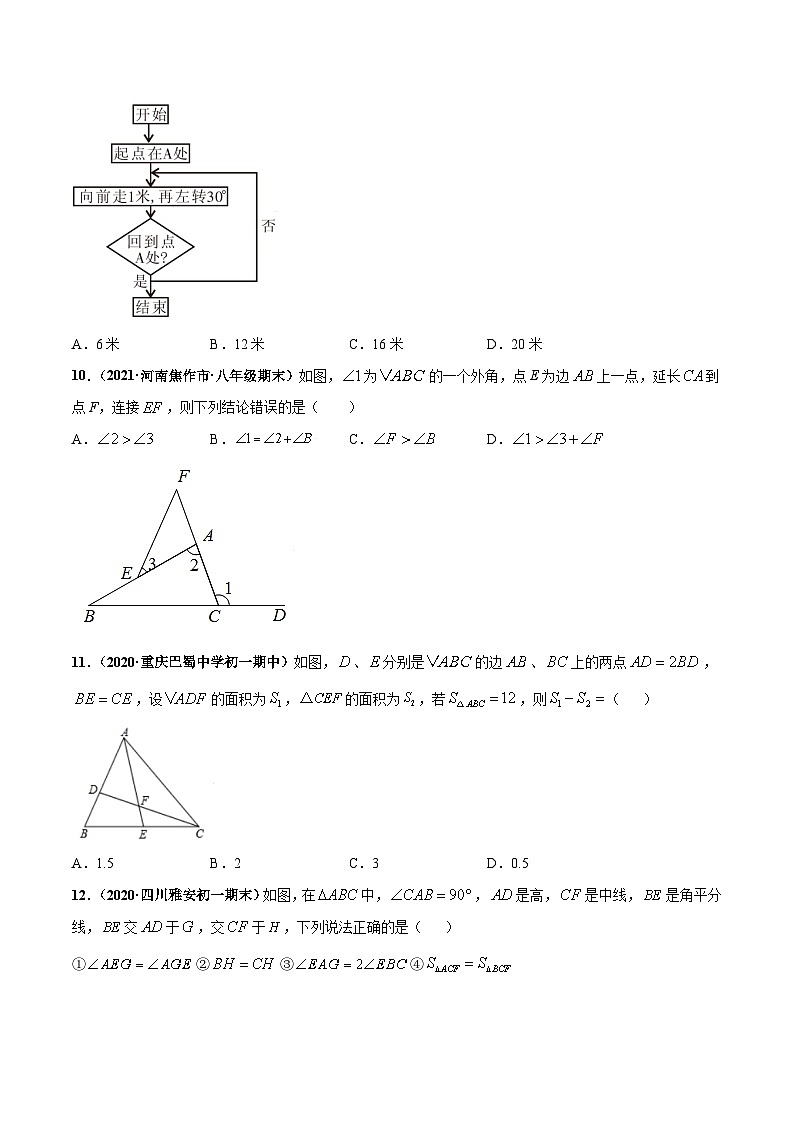
9．（2021·福建莆田市·九年级一模）科技馆为某机器人编制了一个程序，如果机器人在平地上按照图中所示的程序行走，那么该机器人所走的总路程为（    ）

A．6米 B．12米 C．16米 D．20米

10．（2021·河南焦作市·八年级期末）如图，为的一个外角，点E为边上一点，延长到点F，连接，则下列结论错误的是（    ）

A． B． C． D．

11．（2020·重庆巴蜀中学初一期中）如图，、分别是的边、上的两点，，设的面积为，的面积为，若，则（    ）

A．1.5 B．2 C．3 D．0.5

12．（2020·四川雅安初一期末）如图，在中，，是高，是中线，是角平分线，交于，交于，下列说法正确的是（    ）

①②③④

A．①③ B．①②③ C．①③④ D．②③④

二、填空题（本大题共6小题，每小题3分，共18分．不需写出解答过程，请把答案直接填写在横线上）

13．（2021·苏州文昌实验中学校八年级期中）如图1，为响应国家新能源建设，某市公交站亭装上了太阳能电池板．当地某一季节的太阳光（平行光线）与水平线最大夹角为，如图2，电池板与最大夹角时刻的太阳光线相垂直，此时电池板与水平线夹角为，要使，而将电池板逆时针旋转度，则为_______．

14．（2020·江苏崇川初一期末）如图，AD是△ABC的角分平线，CE是△ABC的高，∠BAC=60°，∠BCE=50°，点F为边AB上一点，当△BDF为直角三角形时，则∠ADF的度数为____．

15．（2021·山东省青岛第二十六中学八年级期中）如图，△ABC的面积为1．第一次操作：分别延长AB，BC，CA至点A1，B1，C1，使A1B＝AB，B1C＝BC，C1A＝CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1＝A1B1，B2C1＝B1C1，C2A1＝C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过2021，最少经过多少次操作 ___________

16．（2020·福建初三零模）如图，在△ABC中，AD，CE分别为BC，AB边上的高，若BC＝6，AD＝5，CE＝4，则AB的长为____．

17．（2020·江西萍乡初二期末）如图，六边形ABCDEF的六个内角都相等．若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于_________．

18．（2020·云南师大附中初一期末）在四边形中，与的角平分线交于点，，过点作交于点，，，连接，，则___．

三、解答题（本大题共6小题，共46分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

19．（2020·山西孝义初一期末）阅读下列材料，并完成相应任务．

三角形的内角和

小学时候我们就知道三角形内角和是 180度，学习了平行线之后，可以证明三角形内角和是180度，证明方法如下：

如图1，已知：三角形．求证．

证法一：如图2，过点作直线

即三角形内角和是180°

证法二：如图3，延长至，过点作

···

任务：(1)证法一的思路是用平行线的性质得到将三角形内角和问题转化为一个平角，进而得到三角形内角和是180°，这种方法主要体现的数学思想是________(将正确选项代码填入空格处)

A．数形结合思想            B．分类思想            C．转化思想

(2)将证法二补充完整．

20．（2020·吉林宽城初一期末）将三角形纸片沿折叠，使点落在点处．

（感知）如图①，若点落在四边形的边上，则与之间的数量关系是          ．

（探究）如图②，若点落在四边形的内部，则与之间存在怎样的数量关系？请说明理由．

（拓展）如图③，若点落在四边形的外部，，，则的大小为         度．

21.（2020•雁塔区期中）观察并探求下列各问题，写出你所观察得到的结论．（1）如图①，在△ABC中，P为边BC上一点，则BP+PC　 　AB+AC（填“＞”、“＜”或“＝”）（2）将（1）中点P移到△ABC内，得图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由．（3）将（2）中点P变为两个点P1、P2得图③，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．

22．（2021·河南驻马店市·八年级期末）阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“梦想三角形”例如：一个三角形三个内角的度数分别是，，，这个三角形就是一个“梦想三角形”．反之，若一个三角形是“梦想三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍．

（1）如果一个“梦想三角形”有一个角为，那么这个“梦想三角形”的最小内角的度数为          ．

（2）如图，已知，在射线上取一点，过点作交于点，以为端点作射线，交线段于点（点不与、重合），若，判定、是否是“梦想三角形”，为什么？

23．（2021·镇江市外国语学校八年级月考）如图1，已知，A、B两点同时从点O出发，点A沿射线运动，点B沿射线运动．

（1）如图2，点C为三条内角平分线交点，连接、，在点A、B的运动过程中，的度数是否发生变化？若不发生变化，求其值；若发生变化，请说明理由：

（2）如图3，在（1）的条件下，连接并延长，与的角平分线交于点P，与交于点Q．

①与的数量关系为____．②在中，如果有一个角是另一个角的2倍，求的度数．

24.（2020•邕宁区期末）△ABC中，AD是∠BAC的角平分线，AE是△ABC的高．

（1）如图1，若∠B＝40°，∠C＝62°，请说明∠DAE的度数；

（2）如图2（∠B＜∠C），试说明∠DAE、∠B、∠C的数量关系；

（3）如图3，延长AC到点F，∠CAE和∠BCF的角平分线交于点G，求∠G的度数．

25．（2021·浙江杭州市·八年级期中）如图1，含角的直角三角板与含角的直角三角板的斜边在同一直线上，D为的中点，将直角三角板绕点D按逆时针方向旋转，在旋转过程中：

（1）如图2，当________时，；当______时，；

（2）如图③，当直角三角板的边、分别交、的延长线于点M、N时；

①与度数的和是否变化？若不变，求出与度数的和；若变化，请说明理由；

②若使得，求出、的度数，并直接写出此时的度数；

③若使得，求的度数范围．

26.（2020•丰泽区校级期中）如图①，在△ABC中，∠ABC与∠ACB的平分线相交于点P．

（1）如果∠A＝80°，求∠BPC的度数；（2）如图②，作△ABC外角∠MBC、∠NCB的平分线交于点Q，试探索∠Q、∠A之间的数量关系．（3）如图③，延长线段BP、QC交于点E，△BQE中，存在一个内角等于另一个内角的3倍，请直接写出∠A的度数．