河南省豫东名校2022-2023学年上学期理数新高三摸底联考试卷

这是一份河南省豫东名校2022-2023学年上学期理数新高三摸底联考试卷，共21页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题（共12小题，每小题5分，共60分）
1．设全集U=R，若集合A={−1，0，1，2，3，4，5}，B={x||x−2|>1}，则集合A∩(∁UB)=（ ）
A．{1}B．{−1，0，4，5}
C．{1，2，3}D．{0，1，2，3}
2．已知复数z=a+bi(a，b∈R)，若ai2022+2i=1+bi，则|z|=（ ）
A．2B．3C．2D．5
3．已知平面向量a，b满足a=(3，1)，|b|=2，|a+b|=2，则a与b的夹角为（ ）
A．2π3B．π4C．3π4D．5π6
4．“中国剩余定理”又称“孙子定理”，1852年英国来华传教士伟烈亚利将《孙子算法》中“物不知数”问题的解法传至欧洲.1874年，英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”，“中国剩余定理”讲的是一个关于整除的问题，现有这样一个整除问题：将1至2022这2022个数中，能被5除余1且被7除余1的数按由小到大的顺序排成一列，构成数列{an}，则此数列的项数为（ ）
A．58B．57C．56D．55
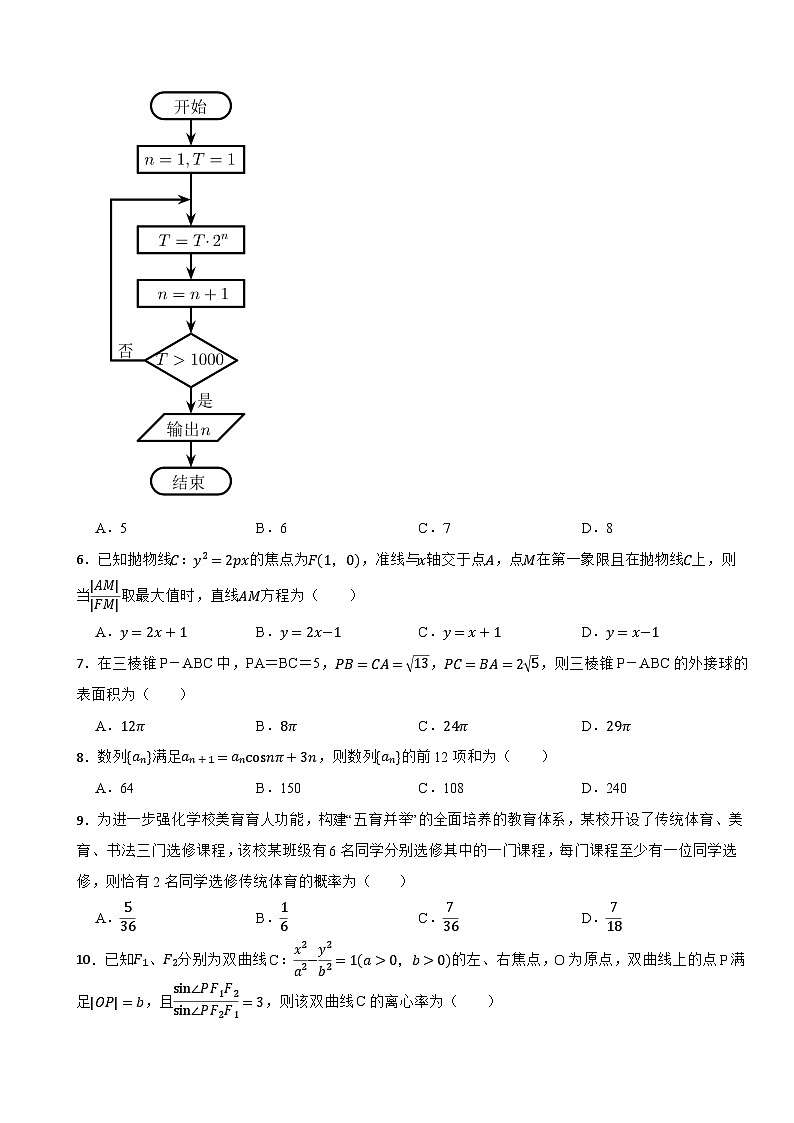
5．已知一个程序框图如图，则输出的n的值等于（ ）
A．5B．6C．7D．8
6．已知抛物线C：y2=2px的焦点为F(1，0)，准线与x轴交于点A，点M在第一象限且在抛物线C上，则当|AM||FM|取最大值时，直线AM方程为（ ）
A．y=2x+1B．y=2x−1C．y=x+1D．y=x−1
7．在三棱锥P－ABC中，PA＝BC＝5，PB=CA=13，PC=BA=25，则三棱锥P－ABC的外接球的表面积为（ ）
A．12πB．8πC．24πD．29π
8．数列{an}满足an+1=ancsnπ+3n，则数列{an}的前12项和为（ ）
A．64B．150C．108D．240
9．为进一步强化学校美育育人功能，构建“五育并举”的全面培养的教育体系，某校开设了传统体育、美育、书法三门选修课程，该校某班级有6名同学分别选修其中的一门课程，每门课程至少有一位同学选修，则恰有2名同学选修传统体育的概率为（ ）
A．536B．16C．736D．718
10．已知F1、F2分别为双曲线C：x2a2−y2b2=1(a>0，b>0)的左、右焦点，O为原点，双曲线上的点P满足|OP|=b，且sin∠PF1F2sin∠PF2F1=3，则该双曲线C的离心率为（ ）
A．2B．62C．2D．3
11．已知f(x)=2x2+3x+1，x≤0|lg2x|，x>0，函数g(x)=f(x)+b有四个不同的零点x1，x2，x3，x4，且满足：x1A．−112．已知正方体ABCD−A1B1C1D1的棱长为2，M，N分别是棱BB1，CD的中点.则下列结论错误的是（ ）
A．若F为棱AB中点，则三棱锥M－NFB的外接球的体积为6π
B．三棱锥A1−MND1在平面D1DCC1上投影为等腰三角形
C．MN//平面A1DC1
D．在棱BC上存在一点E，使得平面AEB1⊥平面MNB
二、填空题（共4小题，每小题5分，共20分）
13．对称美是数学美的重要特征，是数学家追求的目标，也是数学发现与创造中的重要美学因素.著名德国数学家魏尔说：“美和对称紧密相连.”现用随机模拟的方法估算对称蝴蝶（如图中阴影）的面积，将此蝴蝶放在一个宽为2cm，长为3cm的长方形内，并向该长方形内随机投掷1000个点，已知恰有360个点落在阴影区域内，据此可推断蝴蝶的面积是 cm2.
14．已知圆C：x2+y2−4x+3=0，点A，B在圆C上，且|AB|=1，O为原点，则|OA+OB|的最大值为 .
15．已知函数f(x)=sin(ωx−π3)(ω>0)，当|f(x1)−f(x2)|=2时，|x1−x2|的最小值是π3，则函数f(x)在[0，π2]上的单调递减区间为 .
16．设函数f(x)=12x2+2ax(a>0)的图象与g(x)=3a2lnx+b的图象有公共点，且在公共点处的切线重合，则实数b的最大值为 .
三、解答题（共7题，共70分）
17．△ABC中，内角A，B，C的对边分别为a，b，c，且△ABC的外接圆半径R满足RsinC=csC(acsB+bcsA).
（1）求角C；
（2）若c=3，求△ABC周长的取值范围.
18．随着人们生活水平的提高，国家倡导绿色安全消费，菜篮子工程从数量保障型转向质量效益型，为了测试A、B两种不同有机肥料的使用效果，某科研单位用黄瓜做对比实验，分别在两片实验区各摘取100个，对其质量的某项指标值进行检测，质量指数达到45及以上的为“质量优等”，由测量结果绘成频率分布直方图，其中质量指标值分组区间是[30，35)，[35，40)，[40，45)，[45，50)，[50，55].
（1）分别求A实验区黄瓜质量指数的平均数和中位数；（每组数据以区间的中点值为代表，结果保留小数点后一位有效数字）
（2）请根据题中信息完成下面的2×2列联表，并判断是否有99.9%的把握认为“质量优等”与使用肥料有关.
χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，其中n＝a＋b＋c＋d，
19．如图，三棱柱ABC−A1B1C1中，AA1=B1C1，B1C交BC1于点O，AO⊥平面BB1C1C.
（1）求证：AB⊥B1C；
（2）若∠BB1C=30°，且直线AB与平面BB1C1C所成角为60°，求二面角A1−B1C1−A的余弦值.
20．已知椭圆C：x2a2+y2b2=1(a>b>0)，长轴是短轴的3倍，点(1，223)在椭圆C上.
（1）求椭圆C的方程；
（2）若过点Q(1，0)且不与y轴垂直的直线l与椭圆C交于M，N两点，在x轴的正半轴上是否存在点T(t，0)，使得直线TM，TN斜率之积为定值？若存在，求出t的值；若不存在，请说明理由.
21．已知函数f(x)=lnx−kx(k∈R).
（1）若函数f(x)有一个零点，求k的取值范围；
（2）已知函数g(x)=ex，若g(x)−f(x)≥1恒成立，求k的取值范围.
22．在平面直角坐标系xOy中，直线l的参数方程为x=2−3ty=t（t为参数），以坐标原点O为极点，x轴非负半轴为极轴建立极坐标系，曲线C极坐标方程为：ρsin2θ=6csθ.
（1）求直线l普通方程与曲线C的直角坐标方程；
（2）过点M(2，0)的直线l与C相交于A，B两点，求|AM|⋅|BM|的值.
23．已知函数f(x)=|x−2|+|x+1|.
（1）求不等式f(x)≥4的解集；
（2）当x∈R时，若f(x)≥m2−m恒成立，求实数m的取值范围.
答案解析部分
1．【答案】C
【知识点】交、并、补集的混合运算
【解析】【解答】由|x−2|>1，得x−2<−1或x−2>1，
解得x<1或x>3，
所以B={x|x<1或x>3}，
所以∁UB={x|1≤x≤3}，
因为A={−1，0，1，2，3，4，5}，
所以A∩(∁UB)={1，2，3}。
故答案为：C.
【分析】利用已知条件结合绝对值不等式求解方法，进而得出集合B，再利用交集和补集的运算法则，进而得出集合A∩(∁UB)。
2．【答案】D
【知识点】复数相等的充要条件；复数代数形式的乘除运算；复数的模
【解析】【解答】2022=4×505+2，则i2022=i2=−1，ai2022+2i=1+bi，即−a+2i=1+bi，
根据复数相等a=−1b=2，
∴z=−1+2i，|z|=(−1)2+22=5。
故答案为：D.
【分析】利用已知条件结合复数的乘除法运算法则和虚数单位i的周期性，再结合复数相等的判断方法，从而得出a，b的值，进而得出复数z，再结合复数求模公式得出|z|的值。
3．【答案】C
【知识点】平面向量数量积的坐标表示、模、夹角
【解析】【解答】∵|a+b|=2，平方得a2+2a⋅b+b2=2，
∵a=(3，1)，|b|=2，∴a⋅b=−2，设a，b的夹角为θ，其中θ∈[0，π]，可得csθ=a⋅b|a||b|=−222=−22，所以θ=3π4。
故答案为：C.
【分析】利用已知条件结合数量积求向量的模公式，再利用数量积的运算法则得出a→⋅b→的值，设a，b的夹角为θ，其中θ∈[0，π]，再利用数量积求向量的夹角公式得出a，b的夹角θ的值。
4．【答案】A
【知识点】数列的概念及简单表示法；等差数列概念与表示；等差数列的通项公式
【解析】【解答】因为能被5除余1且被7除余1，即能被35除余1的数，
所以a1=1，a2=36，a3=71⋯，即{an}是以1为首项，35为公差的等差数列，
即an=35n−34，
由题意知an=35n−34∈[1，2022]且n∈N∗，得1≤35n−34≤2022，
解得1≤n≤58，n∈N∗，所以此数列的项数为58项。
故答案为：A.
【分析】利用能被5除余1且被7除余1，即能被35除余1的数，所以a1=1，a2=36，a3=71⋯，再利用等差数列的定义判断出数列{an}是以1为首项，35为公差的等差数列，再结合等差数列的通项公式得出an=35n−34，由题意知an=35n−34∈[1，2022]且n∈N∗，从而得出n的取值范围，再利用n∈N∗，从而求出此数列的项数。
5．【答案】A
【知识点】程序框图的三种基本逻辑结构的应用
【解析】【解答】第一次执行，T＝2，n＝2，T<1000，不满足T>1000；
第二次执行T=2×22=23，n＝3，T<1000，不满足T>1000；
第三次执行T=23×23=26，n＝4，T<1000，不满足T>1000；
第四次执行T=26×24=210>1000，n＝5，满足T>1000，跳出循环，n＝5。
故答案为：A.
【分析】利用已知条件结合程序框图的顺序结构、条件结构和循环结构，进而得出输出的n的值。
6．【答案】C
【知识点】直线与圆锥曲线的综合问题
【解析】【解答】过点M作MM1与准线垂直，垂足为M1，|AM||FM|=|AM||MM1|=1cs∠AMM1=1cs∠MAF，如图：
当|AM||FM|最大时，∠MAF取最大值，此时AM与抛物线相切，
∵抛物线的焦点F(1，0)，∴y2=4x，
设切线方程为y=k(x+1)，则y=k(x+1)y2=4x，∴k2x2+(2k2−4)x+k2=0，
由k2≠0Δ=(2k2−4)2−4k4=0解得k2=1，k=±1，
∵点M在第一象限内，∴k=1，直线方程为：y=x+1。
故答案为：C.
【分析】过点M作MM1与准线垂直，垂足为M1，再利用余弦函数的定义得出|AM||FM|=|AM||MM1|=1cs∠MAF，当|AM||FM|最大时，∠MAF取最大值，此时AM与抛物线相切，再利用抛物线的焦点F(1，0)，从而得出p的值，进而得出抛物线的标准方程，设切线方程的点斜式方程为y=k(x+1)，再利用直线与抛物线相交，联立二者方程结合判别式法得出k2≠0Δ=(2k2−4)2−4k4=0，进而得出k的值，再利用点M在第一象限内，从而求出满足要求的k的值，进而得出直线 AM的方程。
7．【答案】D
【知识点】球的体积和表面积
【解析】【解答】三棱锥P－ABC中，PA＝BC＝5，PB=CA=13，PC=AB=25，
构造长方体使得面对角线分别为5，25，13，则长方体体对角线长等于三棱锥外接球直径2R，如图所示，
设长方体棱长分别为a，b，c，则b2+c2=20，a2+b2=25，a2+c2=13，
则a2+b2+c2=29，即4R2=29，外接球表面积4πR2=29π。
故答案为：D
【分析】在三棱锥P－ABC中，PA＝BC＝5，PB=CA=13，PC=AB=25，构造长方体使得面对角线分别为5，25，13，再利用长方体体对角线长等于三棱锥外接球直径2R，设长方体棱长分别为a，b，c，再结合勾股定理得出球的半径长，再利用球的表面积公式得出三棱锥P－ABC的外接球的表面积。
8．【答案】C
【知识点】函数的周期性；数列的求和
【解析】【解答】利用a1=a1，再分别代入n=1，2，3可得a2=−a1+3，a3=a2+6=−a1+9，a4=−a3+9=a1，a1+a2+a3+a4=12.
由csnπ周期为2，同理可得a5+a6+a7+a8=36，a9+a10+a11+a12=60，
∴S12=12+36+60=108。
故答案为：C.
【分析】利用已知条件结合数列的递推公式和函数的周期性，进而结合求和法得出数列{an}的前12项和 。
9．【答案】D
【知识点】古典概型及其概率计算公式；简单计数与排列组合
【解析】【解答】6名同学分别选修一门课程，每门课程至少有一位同学选修，共有(C62C42C22A33+C64+C61C52C33).A33=540种，
恰有2名同学选修传统体育的情况：C62⋅(C41+C42C22A22)⋅A22=210种，
∴P=210540=718。
故答案为：D
【分析】利用已知条件结合组合数公式和排列数公式解决计数问题的方法，再结合古典概型求概率公式，进而得出恰有2名同学选修传统体育的概率。
10．【答案】D
【知识点】双曲线的简单性质；正弦定理；余弦定理
【解析】【解答】因为F1，F2分别为双曲线的左右焦点，
由正弦定理得到|PF2|sin∠PF1F2=|PF1|sin∠PF2F1，
又因为sin∠PF1F2sin∠PF2F1=3得|PF2||PF1|=3，
又∵||PF2|−|PF1||=2a，
∴|PF1|=a，|PF2|=3a，
在△OPF1中，|OF1|=c，|PF1|=a，|OP|=b，
∴∠OPF1=90°，cs∠PF1O=|PF1||OF1|=ac，
在△PF1F2中，cs∠PF1O=a2+4c2−9a22⋅a⋅2c=a2+4c2−9a24ac，
所以a2+4c2−9a24ac=ac，
化简得e=ca=3。
故答案为：D.
【分析】利用F1，F2分别为双曲线的左右焦点，由正弦定理结合sin∠PF1F2sin∠PF2F1=3得|PF2||PF1|的值，再利用双曲线的定义得出|PF1|=a，|PF2|=3a，在△OPF1中，|OF1|=c，|PF1|=a，|OP|=b，再结合双曲线中a，b，c三者的关系式得出∠OPF1=90°，再利用余弦函数的定义得出|PF1||OF1|=ac，在△PF1F2中结合余弦定理得出a，c的关系式，再结合双曲线的离心率公式变形得出双曲线的离心率。
11．【答案】A
【知识点】函数的零点与方程根的关系
【解析】【解答】如图，作出f(x)图象，若y＝－b与y=f(x)有四个交点，需0<−b≤1，则−1≤b<0，A错误，符合题意；
这四个交点的横坐标依次为x1，x2，x3，x4，因为抛物线y=2x2+3x+1的对称轴为x=−34，所以x1+x2=−32，D正确，不符合题意；
因为−lg2x3=lg2x4，即lg2x3+lg2x4=0，所以x3x4=1，B正确，不符合题意；
f(x3)=−lg2x3∈(0，1]，即−1≤lg2x3<0，所以12≤x3<1，C正确，不符合题意.
故答案为：A.
【分析】利用分段函数的解析式作出f(x)图象，若y＝－b与y=f(x)有四个交点，需0<−b≤1，进而得出实数b的取值范围；利用这四个交点的横坐标依次为x1，x2，x3，x4结合物线y=2x2+3x+1的对称轴公式得出其对称轴，再结合中点坐标公式得出x1+x2的值；利用
−lg2x3=lg2x4结合对数的运算法则，进而得出x3x4的值；利用分段函数的解析式和代入法和分段函数的图象以及对数函数的单调性，进而得出x3的取值范围，进而找出结论不正确的选项。
12．【答案】C
【知识点】平行投影及平行投影作图法；球的体积和表面积；直线与平面平行的判定；平面与平面垂直的判定；三角形的形状判断
【解析】【解答】A：在三棱锥M－NFB中，设底面△NBF外接圆的圆心为O1，则C点也在圆O1上，
故三棱锥M－NFB的外接球为三棱锥M－BCF的外接球.
因为BF，BC，BM两两垂直，所以外接球的直径长为CB2+BF2+BM2=22+12+12=6，
所以该球体积为：V=43πR3=6π，正确；
B：三棱锥A1−MND1中，A1与D1在面D1DCC1上的投影为D1，M在面D1DCC1上的投影为棱CC1的中点M1，N在面D1DCC1上的投影为N，
则三棱锥A1−MND1在面D1DCC1上的投影为△D1NM1，
由D1M1=D1N=5得：△D1NM1为等腰三角形，正确；
C：由正方体性质知BD1⊥平面A1DC1，只需判断BD1⋅MN是否为0即可，
建立空间直角坐标系，则B(2，2，0)，D1(0，0，2)，M(2，2，1)，N(0，1，0)，
则BD1=(−2，−2，2)，MN=(−2，−1，−1)，故BD1⋅MN=4≠0，错误；
D：因为BM⊥面ABCD，AE⊂面ABCD，所以BM⊥AE，
当E为棱BC的中点时，AE⊥BN，所以AE⊥平面BMN，
又AE⊂平面AEB1，所以平面AEB1⊥平面BMN，正确.
故答案为：C
【分析】在三棱锥M－NFB中，设底面△NBF外接圆的圆心为O1，则C点也在圆O1上，故三棱锥M－NFB的外接球为三棱锥M－BCF的外接球，利用BF，BC，BM两两垂直，所以用勾股定理得出外接球的直径长，进而得出外接球的半径长，再利用球的体积公式得出该外接球的体积；在三棱锥A1−MND1中，A1与D1在面D1DCC1上的投影为D1，M在面D1DCC1上的投影为棱CC1的中点M1，N在面D1DCC1上的投影为N，则三棱锥A1−MND1在面D1DCC1上的投影为△D1NM1，由D1M1=D1N=5结合等腰三角形的定义判断出三角形△D1NM1为等腰三角形；利用已知条件建立空间直角坐标系，进而得出点的坐标，再结合向量的坐标表示求出向量的坐标，再利用数量积的坐标表示得出BD1⋅MN=4≠0，所以BD1⊥平面A1DC1不成立，所以 MN//平面A1DC1 不成立；利用BM⊥面ABCD结合线面垂直的定义证出线线垂直，所以BM⊥AE，当E为棱BC的中点时，AE⊥BN，再利用线线垂直证出线面垂直，所以AE⊥平面BMN，再利用线面垂直证出面面垂直，所以平面AEB1⊥平面BMN，进而找出结论错误的选项。
13．【答案】2.16
【知识点】几何概型
【解析】【解答】由题意可知，长方形面积为2×3=6cm2，
设图中蝴蝶面积为S，则P=3601000=S6，即S=360×61000=2.16cm2。
故答案为：2.16。
【分析】利用已知条件结合长方形的面积公式和古典概型以及几何概型求概率公式，进而可推断出蝴蝶的面积。
14．【答案】4+3
【知识点】圆方程的综合应用
【解析】【解答】取AB中点D，则OA+OB=2OD，当|OA+OB|最大时，|OD|最大，
由于已知圆C可化为(x−2)2+y2=1，|AB|=1，∴|CD|=AC2−(AB2)2=1−(12)2=32.
所以D在以(2，0)为圆心，半径为32的圆上运动，|OD|max=|OC|+32=2+32，|OA+OB|最大值为4+3。
故答案为：4+3。
【分析】取AB中点D，再利用平行四边形法则，则OA+OB=2OD，当|OA+OB|最大时，|OD|最大，由于已知圆C可化为(x−2)2+y2=1，进而得出|AB|的值，再利用勾股定理得出|CD|的值，再结合圆的定义得出点D在以(2，0)为圆心，半径为32的圆上运动，再结合几何法得出|OD|max的值，进而得出|OA+OB|的最大值。
15．【答案】[5π18，π2]
【知识点】函数的单调性及单调区间
【解析】【解答】由于|f(x1)−f(x2)|=1−(−1)=2，
∴f(x1)，f(x2)中一个取最大值，一个取最小值，|x1−x2|最小值是π3，
可得最小正周期为2π3，而T=2πω=2π3，∴ω=3，则f(x)=sin(3x−π3)，
令2kπ+π2≤3x−π3≤2kπ+3π2(k∈Z)，x∈[2kπ3+5π18，2kπ3+11π18](k∈Z)，
∵x∈[0，π2]，∴x∈[5π18，π2]。
故答案为：[5π18，π2]。
【分析】由于|f(x1)−f(x2)|=1−(−1)=2，所以f(x1)，f(x2)中一个取最大值，一个取最小值，|x1−x2|最小值是π3，可得正弦型函数的最小正周期为2π3，再利用正弦型函数的最小正周期公式得出ω的值，从而得出正弦型函数f(x)的解析式，再利用正弦型函数的图象判断其单调性，进而得出函数f(x)的单调递减区间。
16．【答案】32e23
【知识点】导数的几何意义；利用导数研究函数的单调性；利用导数研究函数最大（小）值
【解析】【解答】设公共点坐标为(x0，y0)，f′(x0)=x0+2a，g′(x0)=3a2x0(x0>0)，
由在公共点处切线相同得x0+2a=3a2x0，即x02+2ax0−3a2=0，解得x0=−3a（舍去）或x0=a，
又y0=f(x0)=g(x0)，即12x02+2ax0=3a2lnx0+b，
所以b=12x02+2ax0−3a2lnx0=52a2−3a2lna(a>0)，
设函数b(a)=52a2−3a2lna(a>0)，
b′(a)=5a−(6alna+3a)=2a−6alna=2a(1−3lna)，
令b′(a)=0得a=e13.
当x∈(0，e13)时，b′(a)>0，当x∈(e13，+∞)时，b′(a)<0.
所以函数b(a)在(0，e13)上单调递增，在(e13，+∞)上单调递减，
所以当a=e13时，b取最大值，将a=e13代入b=52a2−3a2lna，
则得bmax=32e23。
故答案为：32e23。
【分析】设公共点坐标为(x0，y0)，再利用导数求函数在切点处的切线方程的方法结合在公共点处切线相同得出x0+2a=3a2x0，进而得出x0的值，再利用代入法得出y0=f(x0)=g(x0)，所以b=52a2−3a2lna(a>0)，设函数b(a)=52a2−3a2lna(a>0)，再利用求导的方法判断函数的单调性，进而得出函数的最大值，从而得出b的最大值。
17．【答案】（1）解：由正弦定理asinA=bsinB=csinC=2R，可得RsinC=12c，a=2RsinA，b=2RsinB，
∴csC(acsB+bcsA)=2RcsC(sinAcsB+sinBcsA)=2RcsCsin(A+B)=2RcsCsinC=ccsC，
所以ccsC=12c，则csC=12，
因为0（2）解：∵c=3，C=π3，由正弦定理得asinA=bsinB=csinC=332=2，
∴a=2sinA，b=2sinB，
∴△ABC的周长：a+b+c=2sinA+2sinB+3=2sinA+2sin(2π3−A)+3=3sinA+3csA+3=23sin(A+π6)+3，
由A∈(0，2π3)，得A+π6∈(π6，5π6)，∴sin(A+π6)∈(12，1]，
∴a＋b＋c的取值范围(23，33]，即△ABC周长的取值范围是(23，33].
【知识点】两角和与差的正弦公式；含三角函数的复合函数的值域与最值；正弦定理；三角形中的几何计算
【解析】【分析】（1）利用已知条件结合正弦定理和两角和的正弦公式，进而得出角C的余弦值，再利用三角形中角C的取值范围，进而得出角C的值。
（2）利用已知条件结合正弦定理和三角形的周长公式，从而利用辅助角公式化简三角形周长为正弦型函数，再利用 A∈(0，2π3)结合构造法和不等式的基本性质，再结合正弦型函数的图象求值域的方法得出三角形△ABC周长的取值范围。
18．【答案】（1）解：A片实验区黄瓜的质量指数平均数为：
32.5×0.05+37.5×0.15+42.5×0.2+47.5×0.55+52.5×0.05=44.5，
设A片实验区黄瓜质量指数中位数为x，则：0.05+0.15+0.2+(x−45)×0.11=0.5，
得x=451011≈45.9.
（2）解：由题意可得2×2列联表为：
χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=200×(60×70−30×40)2100×100×110×90=20011≈18.182.
∵18.182>10.828，所以有99.9%的把握认为“质量优等”与使用不同的肥料有关.
【知识点】频率分布直方图；众数、中位数、平均数；独立性检验的应用
【解析】【分析】（1）利用已知条件结合频率分布直方图求平均数和中位数的方法，进而分别求出A实验区黄瓜质量指数的平均数和中位数。
（2） 由题意可得2×2列联表，再利用2×2列联表中的数据结合独立性检验的方法判断出有99.9%的把握认为“质量优等”与使用不同的肥料有关。
19．【答案】（1）证明：∵AO⊥平面BB1C1C，B1C⊂平面BB1C1C，∴AO⊥B1C，
∵B1C1=AA1，AA1=BB1，∴B1C1=BB1，∴四边形BB1C1C为菱形，∴B1C⊥BC1，
又BC1∩AO=O，AO⊂平面ABC1，BC1⊂平面ABC1，∴B1C⊥平面ABC1，
∵AB⊂平面ABC1，∴B1C⊥AB.
（2）解：令BC=BB1=2，在等腰△BCB1中，∠BB1C=30°，∴OB＝1，B1C=23，CO=3.
∵AO⊥平面BB1C1C，∴∠ABO为直线AB与平面BB1C1C所成的角，
∴∠ABO＝60°，∴AO=3，
由（1）得OB，OB1，OA两两垂直，所以以O为坐标原点，分别以OB，OB1，OA所在直线分别为x轴，y轴，z轴建立空间直角坐标系，则O(0，0，0)，B(1，0，0)，B1(0，3，0)，A(0，0，3)，C1(−1，0，0)，
则AB1=(0，3，−3)，C1B1=(1，3，0)，A1B1=AB=(1，0，−3)，
设平面AB1C1的一个法向量为n1=(x，y，z)，n1⋅AB1=0n1⋅C1B1=0，∴3y−3z=0x+3y=0.
令y＝1，x=−3，z＝1得n1=(−3，1，1)，
设平面A1B1C1的一个法向量为n2=(x，y，z)，n2⋅A1B1=0n2⋅C1B1=0，∴x−3z=0x+3y=0，
令y＝1，x=−3，z＝－1，解得n2=(−3，1，−1)，
设二面角A1−B1C1−A大小为θ，∵θ为锐角，∴csθ=|cs⟨n1，n2⟩|=|n1⋅n2||n1||n2|=35×5=35.
∴二面角A1−B1C1−A的余弦值为35.
【知识点】空间中直线与直线之间的位置关系；用空间向量研究二面角
【解析】【分析】（1） 利用AO⊥平面BB1C1CB1C⊂结合线面垂直的定义证出线线垂直，所以AO⊥B1C，利用B1C1=AA1，AA1=BB1结合等式的传递性，所以B1C1=BB1，所以四边形BB1C1C为菱形，所以B1C⊥BC1，再利用线线垂直证出线面垂直，所以B1C⊥平面ABC1，再利用线面垂直的定义证出线线垂直，从而证出B1C⊥AB。
（2） 令BC=BB1=2，在等腰△BCB1中，∠BB1C=30°，得出OB＝1，B1C=23，CO=3，再利用AO⊥平面BB1C1C，所以∠ABO为直线AB与平面BB1C1C所成的角，再利用已知条件，进而得出∠ABO的值， 从而得出AO的长，由（1）得OB，OB1，OA两两垂直，所以以O为坐标原点，分别以OB，OB1，OA所在直线分别为x轴，y轴，z轴建立空间直角坐标系，从而得出点的坐标，再结合向量的坐标表示求出向量的坐标，再利用数量积求向量夹角公式得出二面角A1−B1C1−A的余弦值。
20．【答案】（1）解：由题意得a＝3b，故椭圆C为x29b2+y2b2=1，
又点(1，223)在C上，所以19b2+89b2=1，得b2=1，a2=9，
故椭圆C的方程即为x29+y2=1；
（2）解：由已知知直线l过Q(1，0)，设l的方程为x＝my＋1，
联立两个方程得x29+y2=1x=my+1，消去x得：(m2+9)y2+2my−8=0，
Δ=4m2+32(m2+9)>0得m∈R，
设M(x1，y1)，N(x2，y2)，则y1+y2=−2mm2+9，y1y2=−8m2+9（*），
kTM⋅kTN=y1x1−t⋅y2x2−t=y1my1+1−t⋅y2my2+1−t=y1y2m2y1y2+m(1−t)(y1+y2)+(1−t)2，
将（*）代入上式，可得：−8m2+9m2⋅−8m2+9+m(1−t)(−2mm2+9)+(1−t)2=8(9−t2)m2−9(1−t)2，
要使kTM⋅kTN为定值，则有9−t2=0，又∵t>0，∴t＝3，
此时kTM⋅kTN=8−9×4=−29，
∴存在点T(3，0)，使得直线TM与TN斜率之积为定值−29，此时t＝3.
【知识点】椭圆的标准方程；直线与圆锥曲线的综合问题
【解析】【分析】（1）利用已知条件结合长轴和短轴的定义，进而得出a，b的关系式，再利用代入法和椭圆中a，b，c三者的关系式，进而得出a，b，c的值，从而得出椭圆的标准方程。
（2）由已知知直线l过Q(1，0)，设l的方程为x＝my＋1，再利用直线与椭圆相交，联立二者方程结合判别式法得出m的取值范围，设M(x1，y1)，N(x2，y2)，再利用韦达定理得出y1+y2=−2mm2+9，y1y2=−8m2+9（*），再利用两点求斜率公式得出
kTM⋅kTN=y1y2m2y1y2+m(1−t)(y1+y2)+(1−t)2，将（*）代入上式，可得：−8m2+9m2⋅−8m2+9+m(1−t)(−2mm2+9)+(1−t)2=8(9−t2)m2−9(1−t)2，要使kTM⋅kTN为定值，则有9−t2=0，再利用t>0得出t的值，进而得出此时kTM⋅kTN的值，所以存在点T(3，0)，使得直线TM与TN斜率之积为定值−29，此时t＝3。
21．【答案】（1）解：f(x)定义域为(0，+∞)，由于f(x)=lnx−kx有一个零点，可得方程k=lnxx有且仅有一个实根，
令ℎ(x)=lnxx，ℎ′(x)=1−lnxx2，由ℎ′(x)>0得0e，
∴ℎ(x)在(0，e)上单调递增，在(e，+∞)上单调递减，
∴ℎ(x)最大值ℎ(e)=1e，又ℎ(1)=0，∴x∈(0，1)时，ℎ(x)<0；x∈(e，+∞)时，ℎ(x)>0.
画出ℎ(x)=lnxx大致图像如图所示，
若直线y＝k与y=ℎ(x)的图像有一个交点，则k≤0或k=1e.
∴k的取值范围是(−∞，0]∪{1e}.
（2）解：方法一：若g(x)−f(x)≥1恒成立，即ex−lnx+kx≥1恒成立.
∵x>0，∴k≥1+lnx−exx恒成立，只需k≥(1+lnx−exx)max，
令φ(x)=1+lnx−exx，φ′(x)=(1x−ex)x−(1+lnx−ex)x2=ex(1−x)−lnxx2，
令μ(x)=ex(1−x)−lnx(x>0)，μ′(x)=−exx−1x<0，所以μ(x)在(0，+∞)上单调递减，
而μ(1)=0，∴x∈(0，1)，μ(x)>0；x∈(1，+∞)，μ(x)<0，
即x∈(0，1)时，φ′(x)>0，x∈(1，+∞)，φ′(x)<0.
∴φ(x)在(0，1)上单调递增，在(1，+∞)上单调递减.
故φ(x)max=φ(1)=1−e.所以k的取值范围是[1−e，+∞).
方法二：由g(1)−f(1)≥1得k≥1−e，现证明在k≥1−e前提下，原式恒成立.
∵x>0，∴ex−lnx+kx≥ex−lnx+(1−e)x=ex−ex+(x−lnx)（*），
现证明，ex≥ex，x−lnx≥1，构造A(x)=ex−ex，A′(x)=ex−e，
令A′(x)<0解得00解得x>1，
即A(x)在(0，1)上单调递减，在(1，+∞)上单调递增，
∴A(x)≥A(1)=0成立；
构造B(x)=x−lnx，B′(x)=1−1x=x−1x，
令B′(x)<0解得00解得x>1，
即B(x)在(0，1)上单调递减，在(1，+∞)上单调递增，B(x)≥B(1)=1成立，
∴（*）式≥1成立，原式得证.
【知识点】函数恒成立问题；利用导数研究函数的单调性；利用导数研究函数最大（小）值；函数的零点与方程根的关系
【解析】【分析】（1） 利用f(x)定义域为(0，+∞)，由于f(x)=lnx−kx有一个零点，再结合函数的零点与方程的根的等价关系，可得方程k=lnxx有且仅有一个实根，令ℎ(x)=lnxx，再利用求导的方法判断函数的单调性，进而得出函数的最大值，再利用ℎ(1)=0，得出当x∈(0，1)时，ℎ(x)<0；x∈(e，+∞)时，ℎ(x)>0，从而画出ℎ(x)=lnxx大致图象，若直线y＝k与y=ℎ(x)的图像有一个交点，进而结合图象得出实数k的取值范围。
（2）方法一：若g(x)−f(x)≥1恒成立结合x>0，所以k≥1+lnx−exx恒成立，再利用不等式恒成立问题求解方法，只需k≥(1+lnx−exx)max，令φ(x)=1+lnx−exx，再利用求导的方法判断函数的单调性，进而得出函数的最大值，从而得出实数k的取值范围。
方法二：由g(1)−f(1)≥1得k≥1−e，现证明在k≥1−e前提下，原式恒成立，利用x>0得出ex−lnx+kx≥ex−ex+(x−lnx)（*），现证明，ex≥ex，x−lnx≥1，构造A(x)=ex−ex，再利用求导的方法判断函数的单调性，进而得出函数的最小值，所以A(x)≥A(1)=0成立；构造B(x)=x−lnx，再利用求导的方法判断函数的单调性，进而得出函数的最小值，所以B(x)≥B(1)=1成立，所以（*）式≥1成立，原式得证。
22．【答案】（1）解：由于x=2−3ty=t，消t得2−3y=x，即x+3y−2=0，
由ρ⋅sin2θ=6csθ得ρ2⋅sin2θ=6ρcsθ，∴曲线C的直角坐标方程是：y2=6x.
（2）解：将直线l：x=2−3ty=t化为标准形式x=2−32t′y=12t′，
代入y2=6x，(12t′)2=6(2−32t′)并化简得t′2+123t′−48=0.
Δ=624>0，设A，B对应参数为t1，t2，t1t2=−48，所以|AM|⋅|BM|=|t1t2|=48.
【知识点】平面内两点间的距离公式；点的极坐标和直角坐标的互化；参数方程化成普通方程
【解析】【分析】（1）利用已知条件结合参数方程与普通方程的转化方法，再结合极坐标和直角坐标的互化公式，进而得出直线l普通方程与曲线C的直角坐标方程。
（2）利用已知条件，由点斜式方程设出直线l方程，再结合直线l与曲线C相交，联立二者方程求出交点A，B的坐标，再结合已知条件 M(2，0)和两点距离公式得出 |AM|⋅|BM|的值。
23．【答案】（1）解：由于f(x)=|x−2|+|x+1|=−2x+1，x≤−13，−1当x<−1时，−2x+1≥4，解得x≤−32，此时x≤−32；
当−1≤x<2时，3≥4不成立，此时无解；
当x≥2时，2x−1≥4，解得x≥52，此时x≥52.
综上：f(x)≥4的解集为(−∞，−32]∪[52，+∞).
（2）解：∵f(x)=|x−2|+|x+1|≥|(x−2)−(x+1)|=3，当且仅当x∈[−1，2]时等号成立
∴m2−m≤3，即m2−m−3≤0，解得1−132≤m≤1+132.
∴m的取值范围是[1−132，1+132].
【知识点】函数恒成立问题；一元二次不等式及其解法；绝对值三角不等式；含绝对值不等式的解法
【解析】【分析】（1）利用已知条件结合零点分段法，进而求出绝对值不等式f(x)≥4的解集。
（2）利用已知条件结合绝对值三角不等式和不等式恒成立问题求解方法，进而得出 m2−m≤3， 再利用一元二次不等式求解方法，进而得出实数m的取值范围。
A有机肥料
B有机肥料
合计
质量优等



质量非优等



合计



P(x2≥x0)
0.100
0.050
0.010
0.005
0.001
x0
2.706
3.841
6.635
7.879
10.828
A有机肥料
B有机肥料
合计
质量优等
60
30
90
质量非优等
40
70
110
合计
100
100
200