






新高考数学二轮复习考点突破课件 第1部分 专题突破 专题4 第3讲 空间向量与空间角(含解析)
展开以空间几何体为载体考查空间角是高考命题的重点.空间向量是将空间几何问题坐标化的工具,利用空间向量求平面与平面的夹角或线面角是高考热点,通常以解答题的形式出现,难度中等.
(1)(2021·全国乙卷)在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为
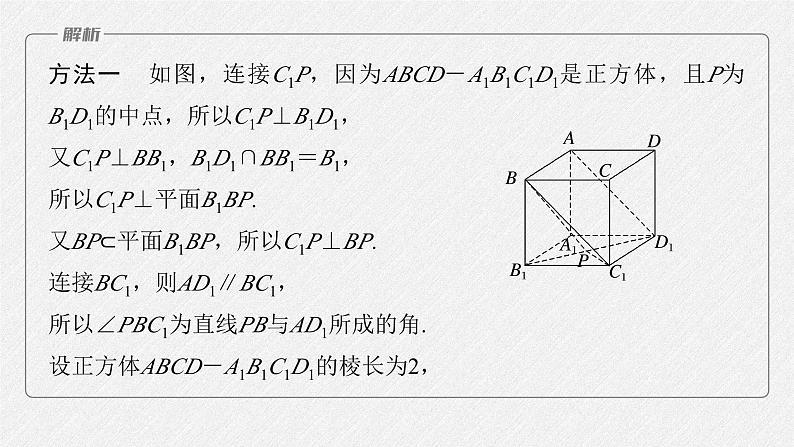
方法一 如图,连接C1P,因为ABCD-A1B1C1D1是正方体,且P为B1D1的中点,所以C1P⊥B1D1,又C1P⊥BB1,B1D1∩BB1=B1,所以C1P⊥平面B1BP.又BP⊂平面B1BP,所以C1P⊥BP.连接BC1,则AD1∥BC1,所以∠PBC1为直线PB与AD1所成的角.设正方体ABCD-A1B1C1D1的棱长为2,
方法二 以B1为坐标原点,B1C1,B1A1,B1B所在的直线分别为x轴、y轴、z轴建立空间直角坐标系(图略),设正方体ABCD-A1B1C1D1的棱长为2,
设直线PB与AD1所成的角为θ,
方法三 如图所示,连接BC1,A1B,A1P,PC1,则易知AD1∥BC1,所以直线PB与AD1所成的角等于直线PB与BC1所成的角.根据P为正方形A1B1C1D1的对角线B1D1的中点,
易知A1,P,C1三点共线,且P为A1C1的中点.易知A1B=BC1=A1C1,所以△A1BC1为等边三角形,
(2)(2022·河南名校联盟联考)在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,它的高为2,AA1,BB1,CC1,DD1均与曲池的底面垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则图中异面直线AB1与CD1所成角的余弦值为
设上底面圆心为O1,下底面圆心为O,连接OO1,OC,OB,O1C1,O1B1,以O为原点,分别以OC,OB,OO1所在直线为x轴、y轴、z轴建立空间直角坐标系,则C(1,0,0),A(0,2,0),B1(0,1,2),D1(2,0,2),
平移线段法求异面直线所成角的步骤(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角.(2)认定:证明作出的角就是所求异面直线所成的角或其补角.(3)计算:求该角的值(常利用解三角形).(4)取舍:由异面直线所成的角的范围确定两条异面直线所成的角.
(1)(2022·南宁模拟)在正方体ABCD-A1B1C1D1中,O为平面AA1B1B的中心,O1为平面A1B1C1D1的中心.若E为CD中点,则异面直线AE与OO1所成角的余弦值为
设正方体的棱长为2,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系,则A(2,0,0),E(0,1,0),O(2,1,1),O1(1,1,2),
设异面直线AE与OO1所成角为θ,
(2)(2022·广东联考)如图,在三棱锥P-ABC中,PA=PB=CA=CB=5,AB=PC=2,点D,E分别为AB,PC的中点,则异面直线PD,BE所成角的余弦值为
如图,连接CD,取CD的中点F,连接EF,BF,则EF∥PD,∠BEF为异面直线PD,BE所成的角.
设直线l的方向向量为a,平面α的法向量为n,直线l与平面α所成的角为θ,
(2022·全国甲卷)在四棱锥P-ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC=CB=1,AB=2,DP=(1)证明:BD⊥PA;
在四边形ABCD中,作DE⊥AB于点E,CF⊥AB于点F,如图.因为CD∥AB,AD=CD=CB=1,AB=2,所以四边形ABCD为等腰梯形,
所以AD2+BD2=AB2,所以AD⊥BD.因为PD⊥平面ABCD,BD⊂平面ABCD,所以PD⊥BD,又PD∩AD=D,PD,AD⊂平面PAD,所以BD⊥平面PAD.又因为PA⊂平面PAD,所以BD⊥PA.
(2)求PD与平面PAB所成角的正弦值.
由(1)知,DA,DB,DP两两垂直,如图,以D为原点建立空间直角坐标系,
设平面PAB的一个法向量为n=(x,y,z),
(1)线面角θ与直线的方向向量a和平面的法向量n所成的角〈a,n〉的关系是〈a,n〉+θ= 所以应用向量法求的是线面角的正弦值,而不是余弦值.(2)利用方程思想求法向量,计算易出错,要认真细心.
(2022·龙岩质检)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,AD⊥DC,PA=PD=PB,BC=DC= AD=2,E为AD的中点,且PE=4.(1)求证:PE⊥平面ABCD;
∴四边形BCDE为平行四边形,∴BE=CD=2,∵PA=PD且E为AD的中点,∴PE⊥AD,
∴PE2+BE2=PB2,即PE⊥BE,又∵AD∩BE=E,AD,BE⊂平面ABCD,∴PE⊥平面ABCD.
以E为原点,EA为x轴,EB为y轴,EP为z轴建立如图所示的空间直角坐标系,则A(2,0,0),B(0,2,0),C(-2,2,0),P(0,0,4),
故可取n=(2,2,1),
设BM=t(t∈[0,2]),则M(-t,2,0),而N(0,0,2),
设直线MN与平面PAB所成的角为θ,
化简得11t2-24t+4=0,
设平面α,β的法向量分别为u,v,平面α与平面β的夹角为θ,
(2022·新高考全国Ⅱ改编)如图,PO是三棱锥P-ABC的高,PA=PB,AB⊥AC,E为PB的中点.(1)证明:OE∥平面PAC;
如图,取AB的中点D,连接DP,DO,DE.因为AP=PB,所以PD⊥AB.因为PO为三棱锥P-ABC的高,所以PO⊥平面ABC.因为AB⊂平面ABC,所以PO⊥AB.又PO,PD⊂平面POD,且PO∩PD=P,所以AB⊥平面POD.因为OD⊂平面POD,所以AB⊥OD,又AB⊥AC,AB,OD,AC⊂平面ABC,所以OD∥AC.
因为OD⊄平面PAC,AC⊂平面PAC,所以OD∥平面PAC.因为D,E分别为BA,BP的中点,所以DE∥PA.因为DE⊄平面PAC,PA⊂平面PAC,所以DE∥平面PAC.又OD,DE⊂平面ODE,OD∩DE=D,所以平面ODE∥平面PAC.又OE⊂平面ODE,所以OE∥平面PAC.
(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求平面CAE与平面AEB夹角的正弦值.
连接OA,因为PO⊥平面ABC,OA,OB⊂平面ABC,所以PO⊥OA,PO⊥OB,
易得在△AOB中,∠OAB=∠ABO=30°,
又∠ABC=∠ABO+∠CBO=60°,
以A为坐标原点,AB,AC所在直线分别为x,y轴,以过A且垂直于平面ABC的直线为z轴建立空间直角坐标系,如图所示,
设平面CAE的法向量为n=(x,y,z),
设平面AEB的法向量为m=(x1,y1,z1),
令z1=2,则m=(0,-3,2),设平面CAE与平面AEB夹角为θ,
(2022·邯郸模拟)如图,在四棱锥P-ABCD中,PA=AB=AD=2,四边形ABCD为平行四边形,∠ABC= ,PA⊥平面ABCD,E,F分别是BC,PC的中点.(1)证明:平面AEF⊥平面PAD.
连接AC(图略).因为PA⊥平面ABCD,所以PA⊥AE,
所以△ABC为等边三角形.又因为E为BC的中点,所以AE⊥BC,又因为AD∥BC,所以AE⊥AD,因为PA∩AD=A,PA,AD⊂平面PAD,所以AE⊥平面PAD,又AE⊂平面AEF,所以平面AEF⊥平面PAD.
(2)求平面AEF与平面AED夹角的余弦值.
以A为原点,AE,AD,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示,
因为PA⊥平面AED,所以n=(0,0,1)是平面AED的一个法向量.设平面AEF的一个法向量为m=(x,y,z),
令z=1,得x=0,y=-2,即m=(0,-2,1).设平面AEF与平面AED夹角为θ,
A.一定不共面B.一定共面C.不一定共面D.无法判断是否共面
2.(2022·温州模拟)在四棱台ABCD-A1B1C1D1中,侧棱AA1与底面垂直,上、下底面均为矩形,AB=1,AD=AA1=A1B1=2,则下列各棱中最长的是A.BB1 B.B1C1C.CC1 D.DD1
由四棱台ABCD-A1B1C1D1可得
因为AA1⊥平面A1B1C1D1,而A1D1,A1B1⊂平面A1B1C1D1,故AA1⊥A1D1,AA1⊥A1B1,而A1D1⊥A1B1,故可建立如图所示的空间直角坐标系.故A1(0,0,0),B(0,1,2),B1(0,2,0),C1(-4,2,0),C(-2,1,2),D(-2,0,2),D1(-4,0,0),
3.如图,在正四棱柱ABCD-A1B1C1D1中,AA1=2AD,E为侧棱DD1上一点,若直线BD1∥平面AEC,则二面角E-AC-B的正切值为
如图,连接BD交AC于点F,连接EF,B1D1,由题意可知,BD1∥EF,因为F为BD的中点,所以E为DD1的中点,又AC⊥平面BDD1B1,BD,EF⊂平面BDD1B1,所以EF⊥AC,BD⊥AC,则∠EFD为二面角E-AC-D的平面角,
又二面角E-AC-B与二面角E-AC-D互补,
4.(2022·菏泽检测)已知三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,侧棱长为3,A1在底面ABC上的射影点D为BC的中点,则异面直线AB与CC1所成角的大小为
如图,连接A1D,AD,A1B,由CC1∥AA1,知∠A1AB为异面直线AB与CC1所成的角,因为三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,且侧棱长为3,A1在底面ABC上的射影点D为BC的中点,
5.(2022·全国甲卷)在长方体ABCD-A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B所成的角均为30°,则A.AB=2ADB.AB与平面AB1C1D所成的角为30°C.AC=CB1D.B1D与平面BB1C1C所成的角为45°
如图,连接BD,易知∠BDB1是直线B1D与平面ABCD所成的角,所以在Rt△BDB1中,∠BDB1=30°,设BB1=1,则B1D=2BB1=2,
易知∠AB1D是直线B1D与平面AA1B1B所成的角,所以在Rt△ADB1中,∠AB1D=30°.
易知∠BAB1是直线AB与平面AB1C1D所成的角,
所以∠BAB1≠30°,所以B项错误;
所以∠DB1C=45°,所以D项正确.
6.向量的运算包含点乘和叉乘,其中点乘就是大家熟悉的向量的数量积.现定义向量的叉乘:给定两个不共线的空间向量a与b,规定:①a×b为同时与a,b垂直的向量;②a,b,a×b三个向量构成右手直角坐标系(如图1);③|a×b|=|a||b|〈a,b〉;④若a=(x1,y1,z1),b=(x2,y2,z2),
如图,建立空间直角坐标系,则D(0,0,0),A(2,0,0),C(0,2,0),B(2,2,0),A1(2,0,3),C1(0,2,3),
二、多项选择题7.(2022·山东联考)若{a,b,c}构成空间的一个基底,则下列向量共面的是A.a+b+c,a-b,2b+cB.a-b,a-c,b-cC.a+2b,a-2b,a+cD.a-2b,6b-3a,-c
选项A,因为a+b+c=(a-b)+(2b+c),所以a+b+c,a-b,2b+c共面;选项B,因为a-b=(a-c)-(b-c),所以a-b,a-c,b-c共面;选项C,a+2b,a-2b在a,b构成的平面内且不共线,a+c不在这个平面内,不符合题意;选项D,因为a-2b,6b-3a共线,所以a-2b,6b-3a,-c共面.
8.(2022·广州模拟)在长方体ABCD-A1B1C1D1中,AB=2,AA1=3,AD=4,则下列命题为真命题的是
对于A,如图,直线AC1与直线CD所成的角,即为直线AC1与直线AB所成的角即∠BAC1,
对于B,构建如图所示的空间直角坐标系,过A的直线l与长方体所有棱所成的角相等,与平面BCC1B1交于M(x,2,z)且x,z>0,
对于D,如图,过A的平面β与长方体所有面所成的二面角都为μ,只需平面β与以4为棱长的正方体中相邻的三条棱顶点所在平面平行,如平面EDF,
三、填空题9.在空间直角坐标系中,设点M是点N(2,-3,5)关于坐标平面Oxy的对称点,点P(1,2,3)关于x轴的对称点为Q,则线段MQ的长度等于______.
因为点M是点N(2,-3,5)关于坐标平面Oxy的对称点,所以M(2,-3,-5),又因为点P(1,2,3)关于x轴的对称点为Q,所以Q(1,-2,-3).
10.如图,矩形ABCD是圆柱O1O2的轴截面,AB=2,AD=3,点E在上底面圆周上,且 ,则异面直线AE与O2C所成角的余弦值为_____.
以O2为坐标原点,O2B,O2O1所在直线分别为y轴、z轴建立如图所示的空间直角坐标系,
11.如图,在二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,若AB=1,AC=2,BD=3,CD= ,则这个二面角的大小为______.
设这个二面角的大小为α,
∴这个二面角的大小为60°.
建立如图所示的空间直角坐标系,且AB=BC=CD=DE=EF=AF=1,由正六边形的性质可得,A(0,0,0),B(1,0,0),
四、解答题13.(2022·莆田质检)如图,在四棱锥P-ABCD中,底面ABCD是菱形,F为PD的中点.(1)证明:PB∥平面AFC;
连接BD交AC于点O,因为ABCD是菱形,所以O为BD的中点.连接OF.因为F为PD的中点,所以OF为△PBD的中位线,所以OF∥PB.因为OF⊂平面AFC,PB⊄平面AFC,所以PB∥平面AFC.
(2)请从下面三个条件中任选一个,补充在横线上,并作答.
若PA⊥平面ABCD,AB=AP=2,且________,求平面ACF与平面ACD夹角的余弦值.注:如果选择多个条件分别解答,按第一个解答计分.
在菱形ABCD中, AC⊥BD.因为AB=AP=2,
设n=(x,y,z)为平面ACF的一个法向量,
显然m=(0,0,1)为平面ACD的一个法向量.设平面ACF与平面ACD的夹角为θ,
14.(2022·湖北联考)如图,已知在四棱锥P-ABCD中,PA⊥平面ABCD,在四边形ABCD中,∠ABC=90°,AB∥CD,AB=1,BC=1,CD=2,点A在平面PCD内的射影恰好是△PCD的重心G.(1)求证:平面PAB⊥平面PBC;
因为PA⊥平面ABCD,BC⊂平面ABCD,所以PA⊥BC,因为∠ABC=90°,所以BC⊥AB,又PA∩AB=A,PA⊂平面PAB,AB⊂平面PAB,所以BC⊥平面PAB,又因为BC⊂平面PBC,所以平面PAB⊥平面PBC.
(2)求直线DG与平面PBC所成角的正弦值.
取CD的中点E,连接AE,因为∠ABC=90°,AB∥CD,AB=BC=1,CD=2,所以四边形ABCE是矩形,所以AB⊥AE,因为PA⊥平面ABCD,AB,AE⊂平面ABCD,所以PA⊥AB,PA⊥AE,所以AB,AE,AP两两垂直,建立如图所示的空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,1,0),E(0,1,0),D(-1,1,0),设P(0,0,t)(t>0),
因为点A在平面PCD内的射影恰好是△PCD的重心G,所以AG⊥平面PCD,又DG⊂平面PCD,所以DG⊥AG,
设m=(x,y,z)是平面PBC的法向量,
设直线DG与平面PBC所成角为θ,
新高考数学二轮复习考点突破课件 第1部分 专题突破 专题5 第3讲 统计与成对数据的分析(含解析): 这是一份新高考数学二轮复习考点突破课件 第1部分 专题突破 专题5 第3讲 统计与成对数据的分析(含解析),共60页。PPT课件主要包含了考情分析,统计图表,考点一,核心提炼,易错提醒,回归分析,考点二,独立性检验,考点三,补充列联表如下等内容,欢迎下载使用。
新高考数学二轮复习考点突破课件 第1部分 专题突破 专题4 第2讲 空间点、直线、平面之间的位置关系(含解析): 这是一份新高考数学二轮复习考点突破课件 第1部分 专题突破 专题4 第2讲 空间点、直线、平面之间的位置关系(含解析),共60页。PPT课件主要包含了考情分析,考点一,核心提炼,规律方法,垂直关系,考点二,翻折问题,考点三,易错提醒,专题强化练等内容,欢迎下载使用。
新高考数学二轮复习考点突破课件 第1部分 专题突破 专题1 第5讲 母题突破3 零点问题(含解析): 这是一份新高考数学二轮复习考点突破课件 第1部分 专题突破 专题1 第5讲 母题突破3 零点问题(含解析),共41页。PPT课件主要包含了母题突破3零点问题,规律方法,专题强化练,由已知得等内容,欢迎下载使用。












