




2023学年二轮复习解答题专题二十八:抛物线上与角度有关问题的探究
展开2023学年二轮复习解答题专题二十八:
抛物线上与角度有关问题的探究
方法点睛
解决角度有关问题的一般步骤:
1、读题,画图,理解题意.
2、分析动点、定点,找不变特征,如角有两边,其中一边是确定的.
3、确定分类特征,进行分类讨论.
4、把角放在直角三角形中,构造相似三角形或全等三角形,根据三角函数、相似或全等的知识解决.
典例分析
例1、(2022达州中考)如图1,在平面直角坐标系中,已知二次函数的图象经过点,,与y轴交于点C.
(1)求该二次函数的表达式;
(2)连接,在该二次函数图象上是否存在点P,使?若存在,请求出点P的坐标:若不存在,请说明理由;
(3)如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线,分别交直线l于点M,N,在点Q的运动过程中,的值是否为定值?若是,请求出该定值;若不是,请说明理由.
【答案】(1)
(2)或
(3)
【解析】
【分析】(1)待定系数法求解析式即可求解;
(2)根据题意,分情况讨论,①过点作关于的对称点,即可求P的坐标,②轴上取一点,使得,则,设,根据勾股定理求得,建列方程,解方程求解即可;
(3)设,,过点作轴于点,则,证明,根据相似三角形的性质列出比例式求得,即可求解.
【小问1详解】
解:∵由二次函数,令,则,
,
过点,,
设二次函数的表达式为,
将点代入得,
,
解得,
,
【小问2详解】
二次函数的图象经过点,,
抛物线的对称轴为,
①如图,过点作关于的对称点,
,
,
,
,
②轴上取一点,使得,则,设,
则,
,
解得,
即,
设直线CD的解析式为,
,
解得,
直线CD的解析式为,
联立,
解得或,
,
综上所述,或,
【小问3详解】
的值是定值,
设,,
过点作轴于点,则,
,
,
,
,
,
即,
,,
,
,
.
即的值是定值
【点睛】本题考查了二次函数综合,待定系数法求解析式,角度问题,相似三角形的性质与判定,掌握二次函数的性质是解题的关键.
专题过关
1. (2022西宁中考)如图,抛物线与x轴交于点,与y轴交于点B,点C在直线AB上,过点C作轴于点,将沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.
(1)求抛物线解析式;
(2)连接BE,求的面积;
(3)拋物线上是否存在一点P,使?若存在,求出P点坐标;若不存在,请说明理由.
【答案】(1)
(2)2 (3)存在,或
【解析】
【分析】(1)先根据翻折得到E点坐标,然后结合运用待定系数法求解即可;
(2)先确定点B的坐标,然后确定直线AB的解析式,进而确定、、,最后根据结合三角形的面积公式即可解答;
(3)先说明是等腰直角三角形,设点P坐标为,然后分点P在x轴上方和下方两种情况分别解答即可.
【小问1详解】
解:∵沿CD所在直线翻折,点A落在点E处
∴
把A,E两点坐标代入得,解得
∴抛物线的解析式为.
【小问2详解】
解:∵抛物线与y轴交于点B
∴令时,
∴
设直线AB的解析式为
把A,B两点坐标代入得解得
∴直线AB的解析式为;
∴点C在直线AB上轴于点
当时
∴
∴
∴,,
∴
∴的面积是2.
【小问3详解】
解:存在,理由如下:
∵,
∴
在中
∴是等腰直角三角形
∵点P在抛物线上
∴设点P的坐标为
①当点P在x轴上方时记为,过作轴于点M
在中∵∴
即解得(舍去)
当时
∴
②当点P在x轴下方时记为,过作轴于点N
在中
∴
∴
∴解得(舍去)
当时
∴
综上,符合条件的P点坐标是或.
【点睛】本题属于二次函数综合题,涉及求二次函数的性质、二次函数解析式、二次函数与几何图形综合等知识点,灵活运用二次函数的性质以及其与几何知识的联系是解答本题的关键.
2.(2022鄂尔多斯中考)(11分)如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A(,0),B(3,)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;
(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【分析】(1)根据待定系数法,将点A,点B代入抛物线解析式,解关于b,c的二元一次方程组,即可求得抛物线的解析式;
(2)设出点P的坐标,确定出PD∥CO,由PD=CO,列出方程求解即可;
(3)过点D作DF⊥CP交CP的延长线于点F,过点F作y轴的平行线EF,过点D作DE⊥EF于点E,过点C作CG⊥EF于点G,证明△DEF≌△FGC(AAS),由全等三角形的性质得出DE=FG,EF=CG,求出F点的坐标,由待定系数法求出直线CF的解析式,联立直线CF和抛物线解析式即可得出点P的坐标.
【解答】解:(1)将点A(﹣,0),B(3,)代入到y=ax2+bx+2中得:
,解得:,
∴抛物线的解析式为y=﹣x2+x+2;
(2)设点P(m,﹣m2+m+2),
∵y=﹣x2+x+2,
∴C(0,2),
设直线BC的解析式为y=kx+c,
∴,解得,
∴直线BC的解析式为y=x+2,
∴D(m,m+2),
∴PD=|﹣m2+m+2﹣m﹣2|=|m2﹣3m|,
∵PD⊥x轴,OC⊥x轴,
∴PD∥CO,
∴当PD=CO时,以P、D、O、C为顶点的四边形是平行四边形,
∴|m2﹣3m|=2,解得m=1或2或或,
∴点P的横坐标为1或2或或;
(3)①当Q在BC下方时,如图,过B作BH⊥CQ于H,过H作MN⊥y轴,交y轴于M,过B作BN⊥MH于N,
∴∠BHC=∠CMH=∠HNB=90°,
∵∠QCB=45°,
∴△BHC是等腰直角三角形,
∴CH=HB,
∴∠CHM+∠BHN=∠HBN+∠BHN=90°,
∴∠CHM=∠HBN,
∴△CHM≌△HBN(AAS),
∴CM=HN,MH=BN,
∵H(m,n),
∵C(0,2),B(3,),
∴,解得,
∴H(,),
设直线CH的解析式为y=px+q,
∴,解得,
∴直线CH的解析式为y=﹣x+2,
联立直线CF与抛物线解析式得,
解得或,
∴Q(,);
②当Q在BC上方时,如图,过B作BH⊥CQ于H,过H作MN⊥y轴,交y轴于M,过B作BN⊥MH于N,
同理得Q(,).
综上,存在,点Q的坐标为(,)或(,).
【点评】此题是二次函数综合题,主要考查了待定系数法求函数解析式,平行四边形的性质,等腰直角三角形的性质和判定,全等三角形的性质和判定,二次函数图象上点的坐标特征,用待定系数法确定出解析式是解本题的关键.
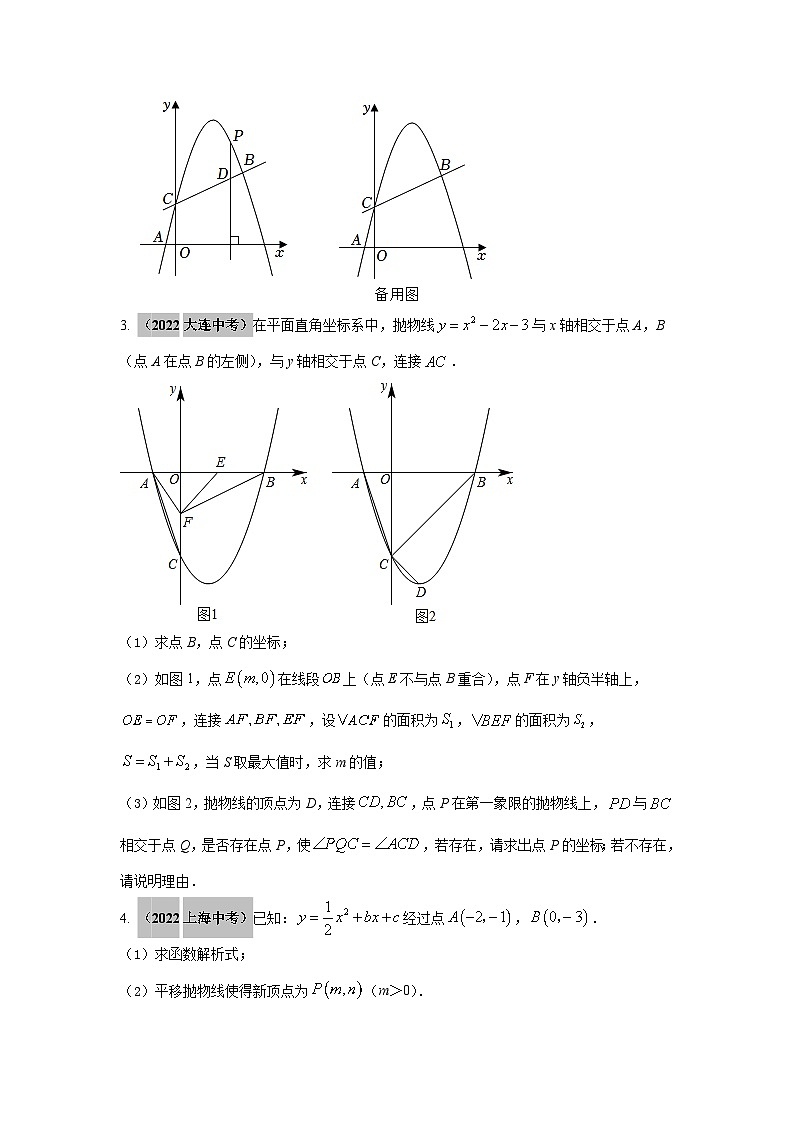
3. (2022大连中考)在平面直角坐标系中,抛物线与x轴相交于点A,B(点A在点B的左侧),与y轴相交于点C,连接.
(1)求点B,点C的坐标;
(2)如图1,点在线段上(点E不与点B重合),点F在y轴负半轴上,,连接,设的面积为,的面积为,,当S取最大值时,求m的值;
(3)如图2,抛物线的顶点为D,连接,点P在第一象限的抛物线上,与相交于点Q,是否存在点P,使,若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)
(2)当最大时,
(3)
【解析】
【分析】(1)利用抛物线的解析式,令x=0,可得C的坐标,令y=0,可得A,C的坐标;
(2)由 可得 再分别表示 再建立二次函数关系式,再利用二次函数的性质可得答案;
(3) 如图,延长DC与x轴交于点N,过A作于H,过作轴于K,连接BD,证明 证明 求解 可得 再求解 及为再联立: 从而可得答案.
【小问1详解】
解:∵,
令 则
令 则
解得:
∴
【小问2详解】
∵
∴
而
∴
∴当最大时,则
【小问3详解】
如图,延长DC与x轴交于点N,过A作于H,过作轴于K,连接BD,
,
∵抛物线
∴顶点
轴,
∴
设为
解得
∴为
联立:
解得:
所以
【点睛】本题考查的是二次函数与坐标轴的交点问题,二次函数的性质,等腰直角三角形的性质,锐角三角函数的应用,利用待定系数法求解一次函数的解析式,函数的交点坐标问题,求解Q的坐标是解本题的关键.
4. (2022上海中考)已知:经过点,.
(1)求函数解析式;
(2)平移抛物线使得新顶点为(m>0).
①倘若,且在的右侧,两抛物线都上升,求的取值范围;
②在原抛物线上,新抛物线与轴交于,时,求点坐标.
【答案】(1)
(2)①k≥2
②P的坐标为(2,3)或(-2,3)
【解析】
【分析】(1)把,代入,求解即可;
(2)①由,得顶点坐标为(0,-3),即点B是原抛物线的顶点,由平移得抛物线向右平移了m个单位,根据,求得m=2,在的右侧,两抛物线都上升,根据抛物线的性质即可求出k取值范围;
②把P(m,n)代入,得n=,则P(m, ),从而求得新抛物线解析式为:y=(x-m)2+n=x2-mx+m2-3,则Q(0,m2-3),从而可求得BQ=m2,BP2=,PQ2=,即可得出BP=PQ,过点P作PC⊥y轴于C,则PC=|m|,根据等腰三角形的性质可得BC=BQ=m2,∠BPC=∠BPQ=×120°=60°,再根据tan∠BPC= tan 60°=,即可求出m值,从而求出点P坐标.
【小问1详解】
解:把,代入,得
,解得:,
∴函数解析式为:;
【小问2详解】
解:①∵,
∴顶点坐标为(0,-3),即点B是原抛物线的顶点,
∵平移抛物线使得新顶点为(m>0).
∴抛物线向右平移了m个单位,
∴,
∴m=2,
∴平移抛物线对称轴为直线x=2,开口向上,
∵在的右侧,两抛物线都上升,
又∵原抛物线对称轴为y 轴,开口向上,
∴k≥2,
②把P(m,n)代入,得n=,
∴P(m, )
根据题意,得新抛物线解析式为:y=(x-m)2+n=x2-mx+m2-3,
∴Q(0,m2-3),
∵B(0,-3),
∴BQ=m2,BP2=,
PQ2=,
∴BP=PQ,
如图,过点P作PC⊥y轴于C,则PC=|m|,
∵BP=PQ,PC⊥BQ,
∴BC=BQ=m2,∠BPC=∠BPQ=×120°=60°,
∴tan∠BPC= tan 60°=,
解得:m=±2,
∴n==3,
故P的坐标为(2,3)或(-2,3)
【点睛】本题考查待定系数法求抛物线解析式,抛物线的平移,抛物线的性质,解直角三角形,等腰三角形的性质,本题属抛物线综合题目,属中考常考试题目,难度一般.
5.(2022南充中考)(12分)抛物线y=x2+bx+c与x轴分别交于点A,B(4,0),与y轴交于点C(0,﹣4).
(1)求抛物线的解析式.
(2)如图1,▱BCPQ顶点P在抛物线上,如果▱BCPQ面积为某值时,符合条件的点P有且只有三个,求点P的坐标.
(3)如图2,点M在第二象限的抛物线上,点N在MO延长线上,OM=2ON,连接BN并延长到点D,使ND=NB.MD交x轴于点E,∠DEB与∠DBE均为锐角,tan∠DEB=2tan∠DBE,求点M的坐标.
【分析】(1)将A、B两点坐标代入抛物线的解析式,从而求得b,c,进而得出抛物线的解析式;
(2)在BC的下方存在一个点P,在BC的上方时两个,其中过BC下方的点P的直线l与BC平行的直线与抛物线相切,根据直线l的解析式与抛物线解析式可以得出一个一元二次方程,该一元二次方程的根的判别式为0,从而求得b的值,进而得出在BC的上方的直线解析式,与抛物线联立成方程组,进一步求得结果;
(3)作MG⊥x轴于G,作NH⊥x轴于H,作MK⊥DF,交DF的延长线于K,设D点的横坐标为a,根据△BHN∽△BFD得出DF=2NH,根据△OMG∽△ONH得出MG=2NH,OG=2OH=a+4,从而KF=MG=DF,根据tan∠DEB=2tan∠DBE可表示出EF,根据△DEF∽△DMK可得出a的值,进一步求得结果.
【解答】解:(1)由题意得,
,
∴,
∴y=﹣;
(2)如图1,
作直线l∥BC且与抛物线相切于点P1,直线l交y轴于E,作直线m∥BC且直线m到BC的距离等于直线l到BC的距离,
∵BC的解析式为y=x﹣4,
∴设直线l的解析式为:y=x+b,
由=x+b得,
x2﹣4x﹣3(b+4)=0,
∵Δ=0,
∴﹣3(b+4)=4,
∴b=﹣,
∴x2﹣4x+4=0,y=x﹣,
∴x=2,y=﹣,
∴P1(2,﹣),
∵E(0,﹣),C(0,﹣4),
∴F(0,﹣4×2﹣(﹣)),
即(0,﹣),
∴直线m的解析式为:y=x﹣,
∴,
∴,,
∴P2(2﹣2,﹣2﹣),P3(2+2,2﹣),
综上所述:点P(2,﹣)或(2﹣2,﹣2﹣)或(2+2,2﹣);
(3)如图2,
作MG⊥x轴于G,作NH⊥x轴于H,作MK⊥DF,交DF的延长线于K,
设D点的横坐标为a,
∵BN=DN,
∴BD=2BN,N点的横坐标为:,
∴OH=,
∵MH∥DF,
∴△BHN∽△BFD,
∴,
∴DF=2NH,
同理可得:△OMG∽△ONH,
∴=,
∴MG=2NH,OG=2OH=a+4,
∴KF=MG=DF,
∵tan∠DEB=2tan∠DBE
∴=2•,
∴EF=,
∵BF=4﹣a,
∴EF=,
∵EF∥MK,
∴△DEF∽△DMK,
∴=,
∴,
∴a=0,
∴OG=a+4=4,
∴G(﹣4,0),
当x=﹣4时,y=﹣﹣4=,
∴M(﹣4,).
【点评】本题考查了求二次函数的解析式,求一次函数的解析式,一次函数和二次函数图象的交点与方程组之间的关系,相似三角形的判定和性质等知识,解决问题的关键是利用相似三角形寻找线段间的数量关系.
6.(2022聊城中考)(12分)如图,在直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C(0,3),对称轴为直线x=﹣1,顶点为点D.
(1)求二次函数的表达式;
(2)连接DA,DC,CB,CA,如图①所示,求证:∠DAC=∠BCO;
(3)如图②,延长DC交x轴于点M,平移二次函数y=﹣x2+bx+c的图象,使顶点D沿着射线DM方向平移到点D1且CD1=2CD,得到新抛物线y1,y1交y轴于点N.如果在y1的对称轴和y1上分别取点P,Q,使以MN为一边,点M,N,P,Q为顶点的四边形是平行四边形,求此时点Q的坐标.
【分析】(1)根据抛物线对称轴和点C坐标分别确定b和c的值,进而求得结果;
(2)根据点A,D,C坐标可得出AD,AC,CD的长,从而推出三角形ADC为直角三角形,进而得出∠DAC和∠BCO的正切值相等,从而得出结论;
(3)先得出y1的顶点,进而得出先抛物线的表达式,从而求得M和N的坐标,点M,N,P,Q为顶点的四边形是平行四边形分为▱MNQP和▱MNPQ,根据M,N和点P的横坐标可以得出Q点的横坐标,进而求得结果.
【解答】(1)解:由题意得,
,
∴,
∴二次函数的表达式为:y=﹣x2﹣2x+3;
(2)证明:∵当x=﹣1时,y=﹣1﹣2×(﹣1)+3=4,
∴D(﹣1,4),
由﹣x2﹣2x+3=0得,
x1=﹣3,x2=1,
∴A(﹣3,0),
∴AD2=25,
∵C(0,3),
∴CD2=2,AC2=18,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴tan∠DAC===,
∵∠BOC=90°,
∴tan∠BCO==,
∴∠DAC=∠BCO;
(3)解:如图,
作DE⊥y轴于E,作D1F⊥y轴于F,
∴DE∥FD1,
∴△DEC∽△D1EF,
∴=,
∴FD1=2DE=2,CF=CE=2,
∴D1(2,1),
∴y1的关系式为:y=﹣(x﹣2)2+1,
由﹣(x﹣2)2+1=0得,
x=3或x=1,
∴M(3,0),
当x=0时,y=﹣3,
∴N(0,﹣3),
设P(2,m),
当▱MNQP时,
∴MN∥PQ,PQ=MN,
∴Q点的横坐标为﹣1,
当x=﹣1时,y=﹣(﹣1﹣2)2+1=﹣8,
∴Q(﹣1,8),
当▱MNPQ时,
同理可得:点Q横坐标为:5,
当x=5时,y=﹣(5﹣2)2+1=﹣8,
∴Q′(5,﹣8),
综上所述:点Q(﹣1,﹣8)或(5,﹣8).
【点评】本题考查了求二次函数的表达式,勾股定理的逆定理,相似三角形的判定和性质,平行四边形的性质和分类等知识,解决问题的关键熟练掌握有关基础知识.
7. (2022泰安中考) 如图,抛物线的图象经过点C,交x轴于点(点A在点B左侧),且连接,D是上方的抛物线一点.
(1)求抛物线的解析式;
(2)连接,,是否存在最大值?若存在,请求出其最大值及此时点D的坐标;若不存在,请说明理由.
(3)第二象限内抛物线上是否存在一点D,垂直于点F,使得中有一个锐角等于与的两倍?若存在,求点D得横坐标,若不存在,请说明理由.
【答案】(1)
(2)存在,的最大值是,
(3)存在,点D的横坐标为或
【解析】
【分析】(1)根据一元二次方程根与系数的关系求得的值进而即可求解;
(2)令y=0,解方程得到x1=-4,x2=1,求得,,进而求得直线解析式,,过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,根据相似三角形的性质即可得到结论;
(3)根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点P,求得P(-,0),得到PA=PC=PB=,过D作x轴的平行线交y轴于R,交AC的延线于G,情况一:如图2,∠DCF=2∠BAC=∠DGC+∠CDG,情况二,∠FDC=2∠BAC,解直角三角形即可得到结论.
【小问1详解】
由,令,即
则
交x轴于点(点A在点B左侧),且
即
解得
抛物线的函数表达式为;
【小问2详解】
由,令,则
解得
则,
令,则
即
设直线的解析式为
则
解得
直线的解析式为
过D作DM⊥x轴交AC于M,过B作BN⊥x轴交AC于N,
∴DM∥BN,
∴△DME∽△BNE,
∴=DE:BE=DM:BN,
设D(a,),
∴M(a,a+2),
∵B(1.0),
∴N(1,),
∴=DM:BN=(-a2-2a):
=-(a+2)2+;
∴当a=-2时,S1:S2的最大值是;,
则;
【小问3详解】
∵A(-4,0),B(1,0),C(0,2),
∴AC=2,BC=,AB=5,
∴AC2+BC2=AB2,
∴△ABC是以∠ACB为直角的直角三角形,
取AB的中点P,
∴P(-,0),
∴PA=PC=PB=,
∴∠CPO=2∠BAC,
∴tan∠CPO=tan(2∠BAC)=,
过作x轴的平行线交y轴于R,交AC的延长线于G,
情况一:如图2,∴∠DCF=2∠BAC=∠DGC+∠CDG,
∴∠CDG=∠BAC,
∴tan∠CDG=tan∠BAC=,
即RC:DR=,
令D(a,-a2-a+2),
∴DR=-a,RC=-a2-a,
∴(-a2-a):(-a)=1:2,
∴a1=0(舍去),a2=-2,
∴xD=-2,
情况二:∴∠FDC=2∠BAC,
∴tan∠FDC=,
设FC=4k,
∴DF=3k,DC=5k,
∵tan∠DGC=3k:FG=1:2,
∴FG=6k,
∴CG=2k,DG=3k
∴,,
∴,
解得a1=0(舍去),a2=-,
综上所述:点D横坐标为-2或-.
【点睛】本题考查了二次函数综合题,一元二次方程根与系数的关系,待定系数法求函数的解析式,相似三角形的判定和性质,解直角三角形,直角三角形的性质等知识点,正确的作出辅助线是解题的关键.
8. (2022通辽中考) 如图,抛物线与轴交于,两点,与轴交于点,直线方程为.
(1)求抛物线的解析式;
(2)点为抛物线上一点,若,请直接写出点的坐标;
(3)点是抛物线上一点,若,求点的坐标.
【答案】(1)y=-x2+4x-3
(2)(,)或(,)或(,)或(,)
(3)(,)
【解析】
【分析】(1)先根据一次函数解析式求出点B、C坐标;再代入,求出b、c 即可求解;
(2)过点A作AN⊥BC于N,过点P作PM⊥BC于M,过点P作PEBC,交y轴于E,交抛物线于p1,p2,过点E作EF⊥BC于F,先求出AN=,再根据两三角形面积关系,求得PM=,从而求得CE=1,则点P是将直线BC向上或向下平移1个单位与抛物线的交点,联立解析式即可求出交点坐标;
(3)过点Q作AD⊥CQ于D,过点D作DF⊥x轴于F财富点C作CE⊥DF于E,证△CDE≌△DAD(AAS),得DE=AF,CE=DF,再证四边形OCEF是矩形,得OF=CE,EF=OC=3,然后设DE=AF=n,则CE=DF=OF=n+1, DF=3-n,则n+1=3-n,解得:n=1,即可求出D(2,-2),用待定系数法求直线CQ解析式为y=x-3,最后联立直线与抛物线解析式,求出交点坐标即可求解.
【小问1详解】
解:对于直线BC解析式y=x-3,
令x=0时,y=-3,
则C(0,-3),
令y=0时,x=3,
则B(3,0),
把B(3,0),C(0,-3),分别代入,得
,解得:,
∴求抛物线的解析式为:y=-x2+4x-3;
【小问2详解】
解:对于抛物线y=-x2+4x-3,
令y=0,则-x2+4x-3=0,解得:x1=1,x2=3,
∴A(1,0),B(3,0),
∴OA=1,OB=3,AB=2,
过点A作AN⊥BC于N,过点P作PM⊥BC于M,如图,
∵A(1,0),B(3,0),C(0,-3),
∴OB=OC=3,AB=2,
∴∠ABC=∠OCB=45°,
∴AN=,
∵,
∴PM=,
过点P作PEBC,交y轴于E,过点E作EF⊥BC于F,
则EF= PM=,
∴CE=1
∴点P是将直线BC向上或向下平移1个单位,与抛物线的交点,如图P1,P2,P3,P4,
∵B(3,0),C(0,-3),
∴直线BC解析式为:y=x-3,
∴平移后的解析式为y=x-2或y=x-4,
联立直线与抛物线解析式,得
或,
解得:,,,,
∴P点的坐标为(,)或(,)或(,)或(,).
【小问3详解】
解:如图,点Q在抛物线上,且∠ACQ=45°,过点Q作AD⊥CQ于D,过点D作DF⊥x轴于F,过点C作CE⊥DF于E,
∵∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴CD=AD,
∵∠E=∠AFD=90°,
∴∠ADF=90°-∠CDE=∠DCE,
∴△CDE≌△DAD(AAS),
∴DE=AF,CE=DF,
∵∠COF=∠E=∠AFD=90°,
∴四边形OCEF是矩形,
∴OF=CE,EF=OC=3,
设DE=AF=n,
∵OA=1,
∴CE=DF=OF=n+1
∴DF=3-n,
∴n+1=3-n
解得:n=1,
∴DE=AF=1,
∴CE=DF=OF=2,
∴D(2,-2),
设直线CQ解析式为y=px-3,
把D(2-2)代入,得p=,
∴直线CQ解析式为y=x-3,
联立直线与抛物线解析式,得
解得:,(不符合题意,舍去),
∴点Q坐标为(,).
【点睛】本题属二次函数与一次函数综合题目,考查了用待定系数法求函数解析式,一次函数图象平行,全等三角形的判定与性质,矩形的判定与性质,熟练掌握一次函数与二次函数的图象性质是解题的关键.
9. (2022呼和浩特中考)如图,抛物线经过点和点,与轴的另一个交点为,连接、.
(1)求抛物线的解析式及点的坐标;
(2)如图1,若点是线段的中点,连接,在轴上是否存在点,使得是以为斜边的直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;
(3)如图2,点是第一象限内抛物线上的动点,过点作轴,分别交、轴于点、,当中有某个角的度数等于度数的2倍时,请求出满足条件的点的横坐标.
【答案】(1);A(-1,0);
(2)存在E(0,3)或(0,-1),使得是以为斜边的直角三角形;
(3)2或
【解析】
【分析】(1)利用待定系数法解答,即可求解;
(2)先根据中点坐标公式可得点,设点E(0,m),再根据两点坐标公式可得,,,再由勾股定理,即可求解;
(3)先求出,再求出直线BC的解析式,然后设点,则,CF=a,可得,再分三种情况讨论:若∠PCM=2∠OBC,过点C作CF∥x轴交PM于点F;若∠PMC=2∠OBC;若∠CPM=2∠OBC,过点P作PG平分∠CPM,则∠MPG=∠OBC,即可求解.
【小问1详解】
解:把点和点代入,得:
,解得:,
∴抛物线的解析式为,
令y=0,则,
解得:,
∴点A(-1,0);
【小问2详解】
解:存在,理由如下:
∵点A(-1,0),点,点是线段的中点,
∴点,
设点E(0,m),
∴,
,
,
∵是以为斜边的直角三角形,
∴,
整理得:,
解得:或-1,
∴点E的坐标为(0,3)或(0,-1);
【小问3详解】
解:∵点B(4,0),C(0,2),
∴OB=4,OC=2,
∴,
设直线BC的解析式为,
把点B(4,0),C(0,2)代入得:
,解得:,
∴直线BC的解析式为,
设点,则,CF=a,
∴,
若∠PCM=2∠OBC,过点C作CF∥x轴交PM于点F,如图甲所示,
∴∠FCM=∠OBC,即,
∴∠PCF=∠FCM,
∵轴,
∴CF⊥PQ,
∴PM=2FM,
∴,
∴,解得:解得:a=2或0(舍去),
∴点P的横坐标为2;
若∠PMC=2∠OBC,
∵∠PMC=∠BMN,
∴∠BMN=2∠OBC,
∵∠OBC+∠BMN=90°,
∴∠OBC=30°,与相矛盾,不合题意,舍去;
若∠CPM=2∠OBC,如图乙所示,过点P作PG平分∠CPM,则∠MPG=∠OBC,
∵∠PMG=∠BMN,
∴△PMG∽△BMN,
∴∠PGM=∠BNM=90°,
∴∠PGC=90°,
∵PG平分∠CPM,即∠MPG=∠CPG,
∴∠PCM=∠PMC,
∴PC=PM,
∴,
解得:或0(舍去),
∴点P的横坐标为;
综上所述,点P的横坐标为2或.
图甲 图乙
【点睛】本题主要考查了二次函数的综合题,解直角三角形,相似三角形的判定和性质,熟练掌握二次函数的综合题,直角三角形的性质,相似三角形的判定和性质,利用数形结合思想和分类讨论思想解答是解题的关键.
10. (2022盘锦中考)如图,抛物线与x轴交于两点(A在B的左侧),与y轴交于点,点P在抛物线上,连接.
(1)求抛物线的解析式;
(2)如图1,若点P在第四象限,点D在线段上,连接并延长交x轴于点E,连接,记的面积为,的面积为,当时,求点P的坐标;
(3)如图2,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段交于点G,当时,求点P的横坐标.
【答案】(1)
(2)
(3)点P的横坐标为
【解析】
【分析】(1)将将、两点代入即可求解;
(2)设点,由,可得即可求解;
(3)作CE⊥l,PQ⊥BC,PN⊥x轴,连接PC交x轴于点H,设,PC的表达式为:,由P,C代入得,PC的表达式,由可表示PQ、PB,分别求EF、CF,由,PQ⊥BC,CE⊥l,证即可求解;
【小问1详解】
解:将、两点代入得,
,解得:
∴抛物线的解析式为:
【小问2详解】
由可得,
设点
则
∵,
∴
∴
解得:(舍去)
∴
【小问3详解】
如图,作CE⊥l,PQ⊥BC,PN⊥x轴,连接PC交x轴于点H,
设,PC的表达式为:,
将P,C代入得,
解得:
PC的表达式为:,
将y=0代入得,,即,
∴
∵
∴
∵
∴
∵
由题可知,
∴
将代入得,,
∴
∴
∵,PQ⊥BC,CE⊥l,
∴
∴
∴
解得:(舍去).
【点睛】本题主要考查二次函数的综合应用,一次函数的应用,三角形的相似,勾股定理,掌握相关知识正确构造辅助线是解题的关键.
11.(2022无锡中考) 已知二次函数图像的对称轴与x轴交于点A(1,0),图像与y轴交于点B(0,3),C、D为该二次函数图像上的两个动点(点C在点D的左侧),且.
(1)求该二次函数的表达式;
(2)若点C与点B重合,求tan∠CDA的值;
(3)点C是否存在其他的位置,使得tan∠CDA的值与(2)中所求的值相等?若存在,请求出点C的坐标;若不存在,请说明理由.
【答案】(1)
(2)1 (3),,
【解析】
【分析】(1)二次函数与y轴交于点,判断,根据,即二次函数对称轴为,求出b的值,即可得到二次函数的表达式;
(2)证明,得到,即,设,点D在第一象限,根据点的坐标写出长度,利用求出t的值,即可,的值,进一步得出tan∠CDA的值;
(3)根据题目要求,找出符合条件的点C的位置,在利用集合图形的性质,求出对应点C的坐标即可。
【小问1详解】
解:∵二次函数与y轴交于点,
∴,即,
∵,即二次函数对称轴为,
∴,
∴,
∴二次函数表达式为.
【小问2详解】
解:如图,过点D作x轴的垂线,垂足为E,连接BD,
∵,
∴,
∵,
∴,
∵,
∴,
∴,即,
∵,,
∴,,
设:,点D在第一象限,
∴,,,
∴,
解得:(舍),(舍),
当时,,
∴,,
∴,
∵在中,
∴
【小问3详解】
解:存在,
如图,(2)图中关于对称轴对称时,,
∵点D的坐标为,
∴此时,点C的坐标为,
如图,当点C、D关于对称轴对称时,此时AC与AD长度相等,即,
当点C在x轴上方时,
过点C作CE垂直于x轴,垂足为E,
∵,点C、D关于对称轴对称,
∴,
∴为等腰直角三角形,
∴,
设点C的坐标为,
∴,,
∴
解得:,(舍),
此时,点C的坐标为,
当点C在x轴下方时,
过点C作CF垂直于x轴,垂足为F,
∵,点C、D关于对称轴对称,
∴,
∴为等腰直角三角形,
∴,
设点C的坐标为,
∴,,
∴
解得:(舍),,
此时,点C的坐标为,
综上:点C的坐标为,,.
【点睛】本题考查二次函数的综合问题,运用数形结合、分类讨论及方程思想是解题的关键.
12. (2022苏州中考) 如图,在二次函数(m是常数,且)的图像与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC,BD.
(1)求A,B,C三点的坐标(用数字或含m的式子表示),并求的度数;
(2)若,求m的值;
(3)若在第四象限内二次函数(m是常数,且)的图像上,始终存在一点P,使得,请结合函数的图像,直接写出m的取值范围.
【答案】(1)A(-1,0);B(2m+1,0);C(0,2m+1);
(2)
(3)
【解析】
【分析】(1)分别令等于0,即可求得的坐标,根据,即可求得;
(2)方法一:如图1,连接AE.由解析式分别求得,,.根据轴对称的性质,可得,由,建立方程,解方程即可求解.方法二:如图2,过点D作交BC于点H.由方法一,得,.证明,根据相似三角形的性质建立方程,解方程即可求解;
(3)设PC与x轴交于点Q,当P在第四象限时,点Q总在点B的左侧,此时,即.
【小问1详解】
当时,.
解方程,得,.
∵点A在点B的左侧,且,
∴,.
当时,.
∴.
∴.
∵,
∴.
【小问2详解】
方法一:如图1,连接AE.
∵,
∴,.
∴,,.
∵点A,点B关于对称轴对称,
∴.
∴.
∴.
∵,,
∴,
即.
∵,
∴.
∴.
∵,
∴解方程,得.
方法二:如图2,过点D作交BC于点H.
由方法一,得,.
∴.
∵,
∴,
.
∴.
∵,,
∴.
∴.
∴,即.
∵,
∴解方程,得.
【小问3详解】
.
设PC与x轴交于点Q,当P在第四象限时,点Q总在点B的左侧,此时,即.
∵,
∴.
,
,
∴.
解得,
又,
∴.
【点睛】本题考查了二次函数综合,求二次函数与坐标轴的交点,角度问题,解直角三角形,相似三角形的性质,三角形内角和定理,综合运用以上知识是解题的关键.
13. (2022十堰中考) 已知抛物线与轴交于点和点两点,与轴交于点.
(1)求抛物线的解析式;
(2)点是抛物线上一动点(不与点,,重合),作轴,垂足为,连接.
①如图1,若点在第三象限,且,求点的坐标;
②直线交直线于点,当点关于直线的对称点落在轴上时,求四边形的周长.
【答案】(1)
(2)①;②或
【解析】
【分析】(1)把点,代入,即可求解;
(2)①过点C作CQ⊥DP于点Q,可得△CPQ为等腰直角三角形,从而得到PQ=CQ,设点,则OD=-m,,再由四边形OCQD为矩形,可得QC=OD=PQ=-m,DQ=OC=3,从而得到,即可求解;②过点E作EM∥x轴于点M,先求出直线BC的解析式为,证得四边形为菱形,可得,然后根据△CEM∽△CBO,设点,则点,然后分三种情况讨论,即可求解.
【小问1详解】
解:把点,代入得:
,解得:,
∴抛物线解析式为;
【小问2详解】
解:①如图,过点C作CQ⊥DP于点Q,
∵点C(0,-3),
∴OC=3,
∵,
∴△CPQ为等腰直角三角形,
∴CQ=PQ,
设点,则OD=-m,,
∵轴,
∴∠COD=∠ODQ=∠CQD=90°,
∴四边形OCQD为矩形,
∴QC=OD=PQ=-m,DQ=OC=3,
∴,
∴,
解得:或0(舍去),
∴点;
②如图,过点E作EM∥x轴于点M,
令y=0,,
解得:(舍去),
∴点B(-4,0),
∴OB=4,
∴,
设直线BC的解析式为,
把点B(-4,0),C(0,-3)代入得:
,解得:,
∴直线BC解析式为,
∵点关于直线的对称点落在轴上时,
∴,,,
∵DP⊥x轴,
∴PD∥CE′,
∴,
∴,
∴CE=PE,
∴,
∴四边形为菱形,
∵EM∥x轴,
∴△CEM∽△CBO,
∴,
设点, 则点,
当点P在y轴左侧时,EM=-t,
当-4<t<0时,,
∴,
∴,
解得:或0(舍去),
∴,
∴四边形的周长为;
当点P在y轴右侧时,EM=-t,
当t≤-4时,,
∴,解得:或0(舍去),
此时,
∴四边形的周长为;
当点P在y轴右侧,即t>0时,EM=t,,
∴,解得:或0,
不符合题意,舍去;
综上所述,四边形的周长为或.
【点睛】本题主要考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、对称的性质和菱形的判定方法;会利用待定系数法求函数解析式;理解坐标与图形性质;会利用相似比计算线段的长和解一元二次方程是解题的关键.
14. (2022黄冈中考) 抛物线y=x2-4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)直接写出点B和点D的坐标;
(2)如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;
(3)如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2,求的最大值.
【答案】(1)B(5,5),D(2,-4);
(2),;
(3);
【解析】
【分析】(1)将两函数解析式联立可求得B点坐标,将一般式转换为顶点式可求出D点坐标;
(2)如图所示,过D作DE⊥x轴与点E,则E(2,0),则tan∠EDO=,当P在E上时,则满足tan∠PDO=,则,如图所示,当时,过D作于点G,由,可得OG=OE=2,DG=DE=4,设,则, ,解出可得n的值进而可求出P的坐标;
(3)由题易得:M(-1,5),,直线MQ的解析式为:,令,解得,则,由BM=6,可知,,,则,求出此二次函数的最值即可.
【小问1详解】
解:将y=x2-4x与y=x联立得:x=x2-4x,
解得:x=5或x=0(舍去),
将x=5代入y=x得y=5,
故B点坐标为(5,5),
将函数y=x2-4x转换为顶点式得,故顶点D为(2,-4),
故B(5,5),D为(2,-4);
【小问2详解】
如图所示,过D作DE⊥x轴与点E,
则E(2,0),则tan∠EDO=,当P在E上时,则满足tan∠PDO=,
则,
如图所示,当时,过O作于点G,
∵,
∴OG=OE=2,DG=DE=4,
设,则,
则,
则或n=0(舍去),
则,则
综上所述,;
【小问3详解】
解:由题易得:M(-1,5),,
则直线MQ的解析式为:,
令,解得,
∴,
∵BM=6,
∴,
且,,
∴,
∵,函数开口向下,
当时,取最大值为.
【点睛】本题考查二次函数的综合,三角函数,数形结合思想,能够根据需要构造适合的辅助线是解决本题的关键.
15.(2022周口扶沟二模) 已知,在平面直角坐标系中,抛物线(m为常数)的顶点为D.
(1)求顶点D的坐标.(用含m的式子表示)
(2)连接OD,若OD与x轴所夹锐角为45°,求m的值.
(3)在(2)的条件下,若,点P在y轴上,将点P向右平移4个单位长度得到点Q,若线段PQ与此抛物线只有一个交点,请直接写出点Q的纵坐标的取值范围.
【答案】(1)(m,4m-3)
(2)m=1或
(3)或
【解析】
【分析】(1)将二次函数解析式化为顶点式即可求解;
(2)根据题意可得点在上,则,解绝对值方程即可求解;
(3)根据题意分经过顶点的情形和不经过顶点的情形分类讨论,即可求解.
【小问1详解】
解:∵,
∴顶点D的坐标为(m,4m-3).
【小问2详解】
∵OD与x轴所夹锐角为45°,且点D(m,4m-3)
∴
∴m=4m-3或m+4m-3=0,
解得m=1或.
【小问3详解】
m=1或,
,则抛物线的顶点D的坐标为
点P在y轴上,将点P向右平移4个单位长度得到点Q,若线段PQ与此抛物线只有一个交点,
当线段PQ经过顶点时,
当线段PQ与此抛物线只有一个交点,则时,与抛物线只有1个交点
令,则,则
综上所述或
【点睛】本题考查了二次函数的性质,化为顶点式,根据自变量的范围求函数值的范围,数形结合是解题的关键.
16. (2022信阳一模)如图,抛物线y=-x²+bx+c与x轴交于点A(-1,0)和B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)若P为抛物线的顶点,动点Q在y轴右侧的抛物线上,是否存在点Q使∠QCO=∠PBC?若存在,请求出点Q的坐标.若不存在,请说明理由.
【答案】(1)
(2)
【解析】
【分析】(1)把点A、B的坐标分别代入二次函数关系式得关于b、c的方程组,解方程组即可;
(2)设CQ与x轴交于点D,先求出、、得出△PBC为直角三角形,得出,根据相似三角形性质得出OD的长,即得出D点的坐标,求出CD的关系式,与二次函数关系式联立方程组,求出点Q的坐标即可.
【小问1详解】
把点A、B的坐标分别代入二次函数关系式得:
,
解得:,
∴抛物线的解析式为;
【小问2详解】
,
把代入得:,
∴顶点P的坐标为(1,4),
∵,
,
,
∴,
∴△PBC为直角三角形,
设CQ与x轴交于点D,如图所示:
∵∠QCO=∠PBC,∠COD=∠PCB,
∴,
∴,
即,
解得:,
∴点D的坐标为(1,0),
设CD关系式为:,把C(0,3),D(1,0),代入得:
,解得:,
∴CD关系式为:,
联立,解得:(舍去),,
把代入得:,
∴点Q的坐标为(5,-12).
【点睛】本题是二次函数的综合,主要考查求二次函数解析式,求一次函数解析式,相似三角形的判定与性质等知识,求出CQ与x轴的交点坐标是解题的关键.
17. (2022河南新野一模)如图,抛物线经过点,与x轴负半轴交于点B,与y轴负半轴交于点,直线经过A、B两点.
(1)求抛物线的解析式;
(2)观察图象,直接写出不等式的解集;
(3)在y轴上是否存在点D,使?如果存在,直接写出点D的坐标;如果不存在,请说明理由.
【答案】(1);
(2);
(3)存在点的坐标是或.
【解析】
【分析】(1)先求出点B、C的坐标,把、、三点代入抛物线,可得抛物线的解析式;
(2)观察函数图象,写出二次函数在一次函数图象下方所对应的自变量的取值范围即可;;
(3)分两种情况进行讨论:①点D在y轴的正半轴上,;②若点D在y轴的负半轴上.
【小问1详解】
直线经过.代入得.
故直线解析式为.
令时,,
∴,故.
∵抛物线经过、、三点,
∴,解得,
∴抛物线的解析式是.
【小问2详解】
由图象可得不等式的解集为.
【小问3详解】
在轴上存在点.使,点的坐标是或.
理由:如图.连接,过点作交的延长线于点.
∵点,,
∴轴,
∴,,
∵,
∴,
∴.
假设在y轴上存在点D,使,设点.
若点D在y轴的正半轴上,
∵,
∴,
∴.
∴点;
若点D在y轴的负半轴上,
∴,
∴点.
故在y轴上存在点D.使,点的坐标是或.
【点睛】此题是二次函数的综合题,主要考查了用待定系数法求二次函数的解析式以及二次函数 与一次函数的关系.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解,第三问要注意分类讨论,不要丢解.
18.(2022河南虞城二模) 如图,抛物线交x轴于两点,交y轴于点
(1)求抛物线解析式及A点坐标;
(2)将抛物线向上平移3个单位长度,再向左平移个单位长度,若新抛物线的顶点在内,求m的取值范围;
(3)点P为抛物线上一个动点,若,直接写出点P坐标.
【答案】(1)抛物线的解析式为,
(2)
(3)或
【解析】
【分析】(1)利用待定系数法,即可求解;
(2)根据平移的性质可得新抛物线的顶点坐标为,然后分别求出直线AC和BC的解析式,可得当点M在直线上时,,当点M在直线上时,,即可求解;
(3)过点A作,垂足为E,过点P作轴,垂足为F.先求出,再由,可得,从而得到,进而得到,再根据,可得PF=2AF,然后设,则AF=a-1,分两种情况讨论,即可求解.
【小问1详解】
解:将分别代人,
可得,解得,
∴抛物线的解析式为,
当时,,
∴,,
∴;
【小问2详解】
解∶由(1)知,
∴该抛物线的顶点为(2,-1),
∴将此抛物线向上平移3个单位长度,再向左平移)个单位长度,
∴新抛物线的顶点坐标为,
∵,
设直线的解析式为,
把点代入得:
,解得:
∴直线的解析式为,
同理直线的解析式为,
当点M在直线上时,,解得:,
当点M在直线上时,,解得:,
∴点M在内时, ;
【小问3详解】
解∶ 如图,过点A作,垂足为E,过点P作轴,垂足为F.
∵, ,A(1,0),
∴OB=OC=3,AB=2,
∴,
∵,
∴,解得:,
∵,
∴,
∴,
∵,,
∴∠AEC=∠AFP=90°,
∵,
∴,
∴,
∴,即PF=2AF,
设,则AF=a-1,
①当点P在x轴上方时,,
∴,解得或(舍去),
∴;
②当点P在x轴下方时,
,解得或(舍去),
∴;
综上所述:存在这样的点P有两个,坐标分别为或.
【点睛】本题考查二次函数的综合应用,熟练掌握二次函数的图象及性质,三角形相似的判定与性质,分类讨论解题是关键.
19. (2022河南汝州一模)如图,已知顶点为的抛物线与x轴交于A,B两点,直线过顶点C和点B.
(1)求直线和抛物线的解析式;
(2)抛物线上是否存在点M,使得,若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1);
(2)或;理由见解析
【解析】
【分析】1)把代入直线中解答即可求出直线的解析式;把代入直线解析式得出点的坐标,再利用待定系数法确定函数关系式即可;
(2)分在上方和下方两种情况进行解答即可.
【小问1详解】
解:将代入,
可得:,
直线的解析式为 ,
将代入得: ,
所以点的坐标为 ,
将,代入 中,
可得:,
解得:,
所以二次函数的解析式为:;
【小问2详解】
解:存在,分以下两种情况:
①若在上方,设交轴于点,则 ,
,
设为,代入,可得: ,
联立两个方程可得: ,
解得: ,,
所以;
②若在下方,设交轴于点,则,
,
设 为,代入可得: ,
联立两个方程可得:,
解得:,,
所以,
综上所述 的坐标为或.
【点睛】本题是二次函数的综合题,考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,直角三角形的性质等知识,熟练掌握待定系数法是解题的关键.
20. (2022山西三模)综合与探究
如图,直线与x轴交于点B,与y轴交于点C,抛物线过点B,C,且与x轴交于另一点A,点D为抛物线上一动点,其横坐标为m.
(1)求k,b的值和点A的坐标.
(2)若点D在第一象限,连接交于点E,连接,,当的面积是的面积的一半时,求m的值.
(3)连接,是否存在点D,使得,若存在,直接写出点D的坐标;若不存在,请说明理由.
【答案】(1),,
(2)或
(3)故存在点,使得
【解析】
【分析】(1)根据抛物线过点B,C,且与x轴交于另一点A,求出抛物线与坐标轴交点坐标,利用待定系数法求直线表达式即可;
(2)过点作于,根据,可得,过点作轴交于,根据“8”字形三角形的相似可得,代值求解即可;
(3)当时,过点作轴于,得到,利用相似比列式求解即可.
【小问1详解】
解:抛物线过点B,C,且与x轴交于另一点A,
当时,,即;当时,,解得或,即、,
直线与x轴交于点,与y轴交于点,
,解得,直线表达式为,
,,;
【小问2详解】
解:过点作于,过点作轴交于,即轴,如图所示:
当的面积是的面积的一半时,即,
,即,
轴,
,,
,
,
点D为抛物线上一动点,其横坐标为m,
,
轴,由(1)中直线表达式为,
,
、、、,
,即,解得或;
【小问3详解】
解:)当时,过点作轴于,如图所示:
,
,
,
、、、,
,即,“十字相乘”法得,解得或,
或(与点重合,舍弃),
故存在点,使得.
【点睛】本题考查二次函数综合,涉及到待定系数法求表达式、利用图形面积关系求坐标、相似三角形的判定与性质、解一元二次方程等知识点,熟练掌握二次函数图象与性质,根据题意所求准确作出辅助线是解决问题的关键.
21. (2022运城二模)如图,已知抛物线与x轴交于点,两点,与y轴交于点C,点P是直线BC下方抛物线上一动点,过点P作直线轴,交直线BC于点D,交x轴于点F,以PD为斜边,在PD的右侧作等腰直角.
(1)求抛物线的表达式,并直接写出直线BC的表达式;
(2)设点P的横坐标为m(),在点P运动的过程中,当等腰直角的面积为9时,请求出m的值;
(3)连接AC,该抛物线上是否存在一点M,使,若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.
【答案】(1),
(2)当或6时,的面积为9
(3)存在.点M的坐标为或
【解析】
【分析】(1)利用待定系数法求出抛物线的解析式,再求出点坐标,然后利用待定系数法求直线的表达式即可;
(2)设出、,然后根据两点间距离公式表示出 长,
解法一:再根据等腰三角形的性质列出的面积表达式,结合面积为建立方程求解,即可解决问题;
解法二:利用,根据相似三角形的性质列比例式建立方程求解,即可解决问题;
解法三:根据等腰直角三角形的性质推出,依此建立方程求解,即可解决问题;
(3)分点在的上方和点在的下方两种情况讨论,根据题意画出图形,构造三角形全等,求出直线上的一点坐标,则可利用待定系数法求出直线的解析式,最后和抛物线的解析式联立求解,即可求出点的坐标.
小问1详解】
解:将,分别代入中,
得 解得,
∴该抛物线的表达式为,
当,,
∴,
设直线的解析式为,
∴,
解得,
∴直线的表达式为:;
【小问2详解】
解法一:依题得,,
∴,
过点F作于N,
∵是等腰直角三角形,PD为斜边,
∴
∴,
∴,
∴ ,
∴
解得,,
又∵
∴当或6时,的面积为9;
解法二:依题得,,
∴,
在中,
当时,,
∴ .
∴,
又∵ .
∴ ,
∴为等腰直角三角形,
由勾股定理得,
∴,.
∴即 .
∴,
∴,
解得,,
又∵ ,
∴当或6时,的面积为9;
解法三:解:依题得,,
∴,
过点F作于N,
∵是等腰直角三角形,PD为斜边,
∴,
∴ ,
∴,
∴ ,
∴,
∴(取正),
∴,
解得,,
又∵,
∴当或6时,的面积为9;
【小问3详解】
解:存在,理由如下:
由(2)得为等腰直角三角形,
∴
①如图,当点在的上方时,设与与轴交于一点,
∵,
∴,
∵,
∵,
∴,
∴,
∴,
设直线的函数式为,
则,
解得,
∴,
则,
解得或(舍去),
∴此时点的坐标为;
②如图,当点在的下方时,
过作轴的垂线,过作轴的垂线,两条垂线交于一点,作,交抛物线与点,
由(2)得为等腰直角三角形,
∴,
∴,
即,
∵
∴,
又∵,
∵,
∴四边形正方形,
∵,
∴,
∴,
∴,
∴,
设直线函数式为,
∴,
解得,
∴,
则,
解得或(舍去);
综上所述,点M的坐标为或.
【点睛】本题是二次函数综合题,考查了二次函数与一次函数的交点问题,二次函数的动态几何问题,二次函数与面积的综合,全等三角形的判定和性质,相似三角形的判定和性质以及正方形的性质,解题的关键是能够综合运用所学的数学知识解决问题.
22. (2022山西侯马二模)如图,抛物线经过,两点,与y轴交于点C,P为第四象限内抛物线上一点,过点P作PM⊥x轴于点M,连接AC,AP,AP与y轴交于点D.
(1)求抛物线的函数表达式.
(2)当∠MPA=2∠PAC时,求直线AP的函数表达式.
(3)在(2)的条件下,在抛物线的对称轴上是否存在点E,使以E,M,C为顶点的三角形是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
【答案】(1);
(2);
(3)存在,点E坐标为或或或
【解析】
【分析】(1)把,分别代入,解方程组即可;
(2)先根据平行线的性质得到∠MPA=∠ODA,然后再由三角形外角的性质得到△ADC为等腰三角形,求出点D的坐标,由A、D两点的坐标即可求得直线AP的函数解析式;
(3)先求出M点坐标,设点E的坐标为,用含n的代数式分别表示出,,,然后进行分类谈论依次解出点E对应的坐标.
【小问1详解】
解:把,分别代入,得.
解得.
∴抛物线的函数表达式为;
【小问2详解】
解:根据题意,得.
∴∠MPA=∠ODA.
又∵∠MPA=2∠PAC,∴∠ODA=2∠PAC.
又∵∠ODA=∠DAC+∠ACD,
∴∠DAC=∠ACD.∴CD=AD.
在中,令,解得,∴.
设OD=m,则AD=CD=3-m.
∵,∴OA=1.
在Rt△AOD中,根据勾股定理,得.解得.
∴.
设直线AP的函数表达式为.
把,分别代入,得解得
∴直线AP的函数表达式为;
【小问3详解】
解:存在,点E的坐标为或或或.
令,解得,.
∴点P的横坐标为.
∵PM⊥x轴,∴.
由,得抛物线的对称轴为直线,
由(2)可得.
设点E的坐标为,则,,.
若∠MCE=90°,则,即,解得.
若∠CME=90°,则,即,解得.
若∠CEM=90°,则,即,解得,.
综上所述,点E的坐标为或或或.
【点睛】本题考查的是二次函数的综合题,熟练掌握二次函数的图像与性质,直角三角形的性质是解决问题的关键.
2023学年二轮复习解答题专题三十九:抛物线上最值问题的探究: 这是一份2023学年二轮复习解答题专题三十九:抛物线上最值问题的探究,文件包含2023学年二轮复习解答题专题三十九抛物线上最值问题的探究原卷版docx、2023学年二轮复习解答题专题三十九抛物线上最值问题的探究解析版docx等2份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。
2023学年二轮复习解答题专题三十八:抛物线上旋转问题的探究: 这是一份2023学年二轮复习解答题专题三十八:抛物线上旋转问题的探究,文件包含2023学年二轮复习解答题专题三十八抛物线上旋转问题的探究原卷版docx、2023学年二轮复习解答题专题三十八抛物线上旋转问题的探究解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
2023学年二轮复习解答题专题三十七:抛物线上翻折问题的探究: 这是一份2023学年二轮复习解答题专题三十七:抛物线上翻折问题的探究,文件包含2023学年二轮复习解答题专题三十七抛物线上翻折问题的探究原卷版docx、2023学年二轮复习解答题专题三十七抛物线上翻折问题的探究解析版docx等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。












