新高考数学一轮复习基础巩固8.4 单调性（精讲）（含解析）

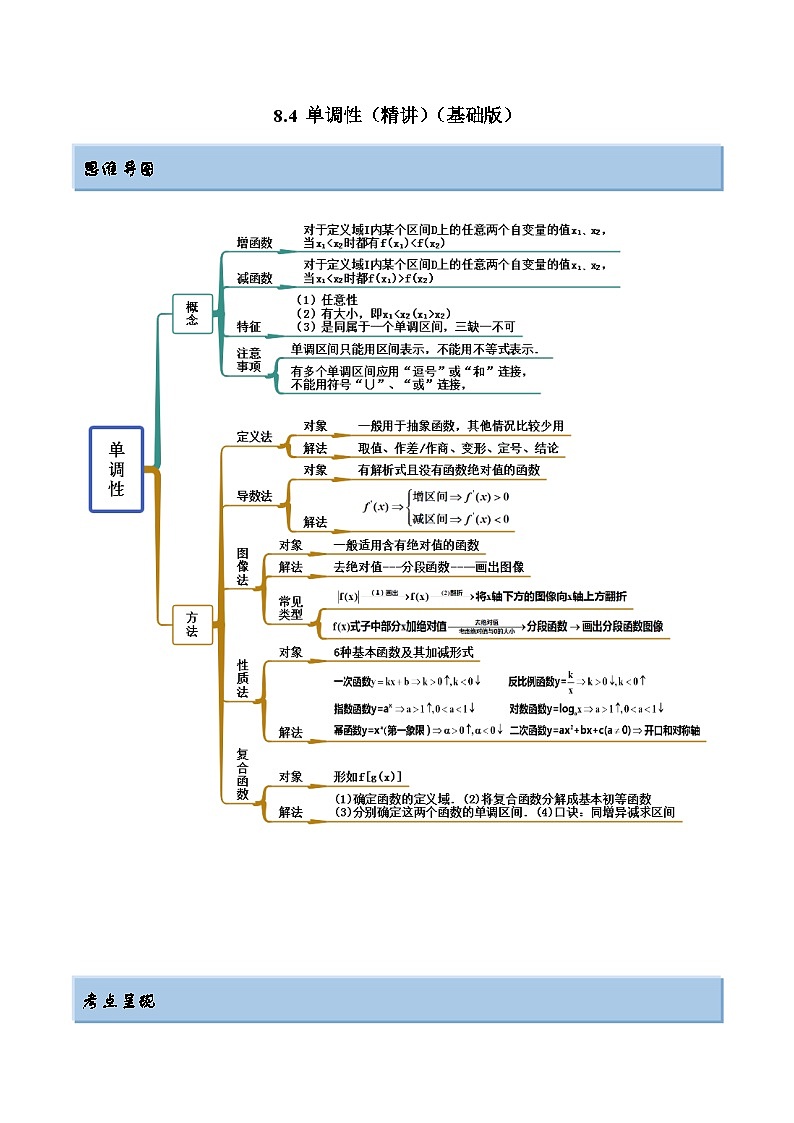
8.4 单调性（精讲）（基础版）

考点一 性质法

【例1-1】（2021·辽宁大连·高三学业考试）下列函数在R上为增函数的是（     ）

A． B．

C． D．

【答案】B

【解析】在上单调递减，在上单调递增，故选项A错误；

在R上为增函数，选项B正确；

在上单调递减，故选项C错误；

在单调递减，在单调递减，故选项D错误.故选：B.

【例1-2】（2021·贵州·贵阳一中高三阶段练习（理））函数的单调递减区间为（       ）

A． B． C． D．

【答案】B

【解析】在函数中，由得或，则的定义域为，

函数在上单调递减，在上单调递增，又在上单调递增，

于是得在上单调递减，在上单调递增，

所以函数的单调递减区间为.故选：B

【一隅三反】

1．（2022·全国·高三专题练习（文））函数的单调递增区间是（       ）

A． B．

C． D．

【答案】C

【解析】令，解得，

令，则，

∵函数在区间上单调递增，在区间上单调递减，在定义域内递增，

∴根据复合函数的单调性可知，函数的单调递增区间是故选：C

2（2022江西）.下列函数中，在其定义域上是减函数的是（    ）

A． B．

C． D．

【答案】D

【解析】A:因为为减函数，所以为增函数；

B: 对称轴为，图象开口向上，所以在上为增函数；

C:因为在定义域上为减函数，所以在定义域上为增函数；

D:当时，为减函数，当时，为减函数，且，

所以在定义域上为减函数.故选:D.

3（2022山东）函数的单调递增区间是________

【答案】

【解析】

当时，单调递减，而也单调递减，所以单调递增，故答案为：

考点二 图像法

【例2-1】（2021·全国·高三专题练习）函数的单调递增区间是（       ）

A．  B． 和

C．和 D． 和

【答案】B

【解析】

如图所示：

函数的单调递增区间是和．

故选：B.

【例2-2】（2020·全国·高三专题练习）函数的单调减区间是（       ）

A． B． C． D．

【答案】A

【解析】直接通过解析式，结合二次函数图象得：递增，在递减，故选：A.

【一隅三反】

1．（2022·全国·高三专题练习）下列关于函数的结论，正确的是（       ）

A．f(x)在(0，+∞)上单调递增            B．f(x)在(0，+∞)上单调递减

C．f(x)在(-∞，0]上单调递增             D．f(x)在(-∞，0]上单调递减

【答案】D

【解析】由题意可得，

作出函数f(x)的图像如图所示，

由图可知，函数f(x)在(-∞，1)上单调递减，在(1，+∞)上单调递增故选：D.

2．（2021·安徽·六安市裕安区新安中学高三阶段练习（理））函数的单调递增区间是（       ）

A． B． C． D．

【答案】B

【解析】，的单调递增区间是.故选：B.

3．（2022·全国·高三专题练习）已知函数，则下列结论正确的是（       ）

A．递增区间是 B．递减区间是

C．递增区间是 D．递增区间是

【答案】D

【解析】因为函数，作出函数的图象，

如图所示：

由图可知，递增区间是，递减区间是和．故选：D．

考点三 导数法

【例3】（2022·全国课时练习）求下列函数的单调区间.

（1）f(x)＝x3－3x＋1；（2）y＝x＋.（3）3；（4）y＝ln(2x＋3)＋x2.

【答案】（1）增区间为(－∞，－1)，(1，＋∞)，减区间是(－1，1)；

（2）增区间为(－∞，-)和(，＋∞)，减区间为(－，0)和(0，).

（3）单调递增区间为(－ ∞，0)，(2，＋∞)，单调递减区间为(0，2)；

（4）单调递增区间为，，单调递减区间为.

【解析】（1）＝3x2－3＝3(x＋1)(x－1)，

令>0，得x>1，或x<－1.令<0，得－1<x<1.

∴f(x)的增区间为(－∞，－1)，(1，＋∞)，减区间是(－1，1).

（2）＝1－＝，

由>0，解得x<－，或x>.由<0，解得－<x<，(x≠0).

∴函数的增区间为(－∞，－)和(，＋∞)，减区间为(－，0)和(0，).

（3）函数的定义域为R.

y′＝2x2－4x＝2x(x－2)．令y′＞0，则2x(x－2)＞0，解得x＜0或x＞2.

所以函数的单调递增区间为(－ ∞，0)，(2，＋∞)．

令y′＜0，则2x(x－2)＜0，解得0＜x＜2.所以函数的单调递减区间为(0，2)．

(4)    函数y＝ln(2x＋3)＋x2的定义域为.y′＝＋2x＝＝.

令y′＞0，解得－＜x＜－1或x＞－.所以函数的单调递增区间为，.

令y′＜0，解得－1＜x＜－，所以函数的单调递减区间为.

【一隅三反】

（2021·全国）求下列函数的单调区间

（1）f(x)＝；（2）y＝x2－ln x．（3）f(x)＝2x3＋3x2－36x＋1；（4）f(x)＝sin x－x(0<x<π)．

（5）；（6）．

【答案】（1）单调递增区间是(－∞，1－)和(1＋，＋∞)；单调递减区间是(1－，1)和(1，1＋) ；（2）单调递增区间为(1，＋∞)；单调递减区间为(0，1) ．

（3）增区间是(－∞，－3)，(2，＋∞)；减区间是(－3，2) ；

（4）单调递减区间为(0，π) ．

（5）函数的单调递减区间为，，单调递增区间为；

（6）单调递增区间为（），单调递减区间（）.

【解析】（1）f(x)的定义域为{x|x∈R且x≠1}，

f′(x)＝＝＝．

令f′(x)>0，解得x>1＋或x<1－；令f′(x)<0，解得1－<x<1或1<x<1＋．

所以f(x)的单调递增区间是(－∞，1－)和(1＋，＋∞)；单调递减区间是(1－，1)和(1，1＋)．

（2）函数y＝x2－ln x的定义域为(0，＋∞)，又y′＝．

若y′>0，即解得x>1；若y′<0，即解得0<x<1．

故函数y＝x2－ln x的单调递增区间为(1，＋∞)；单调递减区间为(0，1)．

（3）＝6x2＋6x－36．由>0得6x2＋6x－36>0，解得x<－3或x>2；

由<0解得 －3<x<2．故f(x)的增区间是(－∞，－3)，(2，＋∞)；减区间是(－3，2)．

（4）＝cos x－1．因为0<x<π，所以cos x－1<0恒成立，故函数f(x)的单调递减区间为(0，π)，无增区间．

（5）由题得函数的定义域为.，

令，即，解得；

令，即，解得或，

故所求函数的单调递减区间为，，单调递增区间为．

（6）由题得函数的定义域为.

令，得，即（），

令，得，即（），

故的单调递增区间为（），单调递减区间（）．

考点四 已知单调性求参数

【例4-1】（2022·河南濮阳·一模（理））“”是“函数是在上的单调函数”的（       ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】B

【解析】依题意，函数是在上的单调函数，

由于在上递增，所以在上递增，

所以且，即.

所以“”是“函数是在上的单调函数”的必要不充分条件.故选:B

【一隅三反】

1．（2022·江西）已知函数，是R上的增函数，则实数a的取值范围是（       ）

A． B．

C． D．

【答案】C

【解析】若是上的增函数，则应满足，解得，即.故选：C

2．（2022·河北·高三阶段练习）函数的最大值为2，且在上单调递增，则a的范围是______，的最小值为______.

【答案】          2

【解析】注意到是减函数，

∴在上单调递减，

而的递减区间是，

∴，.

∵的最大值为2，

∴的最小值为，

即，，

令，，，

∴在处取得最小值2.

故答案为：，2

3．（2021·上海市进才中学高三阶段练习）已知函数在区间上为增函数，则实数a的取值范围是________．

【答案】

【解析】，因为函数在区间上为增函数，所以，

解得：.故答案为：

4．（2022·全国·高三专题练习（文））若函数y＝|4x－1|在(－∞，k]上单调递减，则k的取值范围为____________．

【答案】(－∞，0]

【解析】函数y＝|4x－1|的图象是由函数y＝4x的图象向下平移一个单位后，再把位于x轴下方的图象沿x轴翻折到x轴上方得到的，函数图象如图所示．

由图象知，其在(－∞，0]上单调递减，所以k的取值范围是(－∞，0]．

故答案为：(－∞，0].

5．（2020·全国·高三专题练习（理））函数在上单调递减，则实数的取值范围是________.

【答案】

【解析】①时，在R上单调递减

∴满足条件；

②时，

对称轴为，解得.

由①②得，故的取值范围是.

故答案为：.