新高考数学一轮复习课时过关练习第03章 一元函数的导数及其应用第3节 导数与函数的极值、最值 (含解析)

这是一份新高考数学一轮复习课时过关练习第03章 一元函数的导数及其应用第3节 导数与函数的极值、最值 (含解析)，共17页。试卷主要包含了函数的最大值，已知f＝eq \f，则f等内容，欢迎下载使用。

第3节　导数与函数的极值、最值
考试要求　1.借助函数图象，了解函数在某点取得极值的必要和充分条件.2.会用导数求函数的极大值、极小值.3.会求闭区间上函数的最大值、最小值.


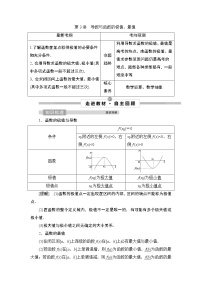
1.函数的极值
(1)函数的极小值：
函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0.则a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值.
(2)函数的极大值：
函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0.则b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值.
(3)极小值点、极大值点统称为极值点，极小值和极大值统称为极值.
2.函数的最大(小)值
(1)函数f(x)在区间[a，b]上有最值的条件：
如果在区间[a，b]上函数y＝f(x)的图象是一条连续不断的曲线，那么它必有最大值和最小值.
(2)求y＝f(x)在区间[a，b]上的最大(小)值的步骤：
①求函数y＝f(x)在区间(a，b)上的极值；
②将函数y＝f(x)的各极值与端点处的函数值f(a)，f(b)比较，其中最大的一个是最大值，最小的一个是最小值.

1.求最值时，应注意极值点和所给区间的关系，关系不确定时，需要分类讨论，不可想当然认为极值就是最值.
2.函数最值是“整体”概念，而函数极值是“局部”概念，极大值与极小值之间没有必然的大小关系.

1.思考辨析(在括号内打“√”或“×”)
(1)对于可导函数f(x)，若f′(x0)＝0，则x0为极值点.(　　)
(2)函数的极大值不一定是最大值，最小值也不一定是极小值.(　　)
(3)函数f(x)在区间(a，b)上不存在最值.(　　)
(4)函数f(x)在区间[a，b]上一定存在最值.(　　)
答案　(1)×　(2)√　(3)×　(4)√
解析　(1)反例：f(x)＝x3，f′(x)＝3x2，f′(0)＝0，但x＝0不是f(x)＝x3的极值点.(3)反例：f(x)＝x2在区间(－1，2)上的最小值为0.
2.如图是f(x)的导函数f′(x)的图象，则f(x)的极小值点的个数为(　　)

A.1 B.2 C.3 D.4
答案　A
解析　由题意知在x＝－1处f′(－1)＝0，且其两侧导数值符号为左负右正.
3.(多选)(2022·青岛月考)已知f(x)＝，则f(x)(　　)
A.在(－∞，＋∞)上单调递减
B.在(－∞，1)上单调递增
C.有极大值，无极小值
D.有极小值，无极大值
答案　BC
解析　由题意知f′(x)＝，当x＜1时，f′(x)＞0，f(x)递增，x＞1时，f′(x)＜0，f(x)递减，f(1)是函数的极大值，也是最大值f(1)＝，函数无极小值.
4.(2021·新乡三模)某冷饮店的日销售额y(单位：元)与当天的最高气温x(单位：℃，20≤x≤40)的关系式为y＝x2－x3，则该冷饮店的日销售额的最大值约为(　　)
A.907元 B.910元 C.915元 D.920元
答案　C
解析　∵y＝x2－x3，20≤x≤40，
∴y′＝x－x2＝－x(x－38).
∴当20≤x≤38时，y′≥0，即函数在[20，38]上单调递增，当38≤x≤40时，y′≤0，即函数在[38，40]上单调递减，∴当x＝38时，函数取值最大值，∴ymax＝×382－×383≈915.
5.(易错题)函数f(x)＝x3－ax2＋2x－1有极值，则实数a的取值范围是________.
答案　(－∞，－)∪(，＋∞)
解析　f′(x)＝3x2－2ax＋2，由题意知f′(x)有变号零点，∴Δ＝(2a)2－4×3×2＞0，解得a＞或a＜－.
6.若函数f(x)＝x3－4x＋m在[0，3]上的最大值为4，则m＝________.
答案　4
解析　f′(x)＝x2－4，x∈[0，3]，当x∈[0，2)时，f′(x)＜0，当x∈(2，3]时，f′(x)＞0，所以f(x)在[0，2)上单调递减，在(2，3]上单调递增.又f(0)＝m，f(3)＝－3＋m.在[0，3]上，f(x)max＝f(0)＝4，所以m＝4.

　考点一　利用导数求函数的极值
角度1　根据函数图象判断极值
例1 (多选)(2022·重庆检测)函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则(　　)

A.－3是函数y＝f(x)的极值点
B.－1是函数y＝f(x)的极小值点
C.y＝f(x)在区间(－3，1)上单调递增
D.－2是函数y＝f(x)的极大值点
答案　AC
解析　根据导函数的图象可知，当x∈(－∞，－3)时，f′(x)<0，当x∈(－3，－1)时，f′(x)>0，所以函数y＝f(x)在(－∞，－3)上单调递减，在(－3，－1)上单调递增，可知－3是函数y＝f(x)的极值点，所以A正确.
因为函数y＝f(x)在(－3，1)上单调递增，可知－1不是函数y＝f(x)的极小值点，－2也不是函数y＝f(x)的极大值点，所以B错误，C正确，D错误.
感悟提升　由图象判断函数y＝f(x)的极值，要抓住两点：(1)由y＝f′(x)的图象与x轴的交点，可得函数y＝f(x)的可能极值点；(2)由导函数y＝f′(x)的图象可以看出y＝f′(x)的值的正负，从而可得函数y＝f(x)的单调性.两者结合可得极值点.
角度2　求已知函数的极值
例2 已知函数f(x)＝ln x－ax(a∈R).
(1)当a＝时，求f(x)的极值；
(2)讨论函数f(x)在定义域内极值点的个数.
解　(1)当a＝时，f(x)＝ln x－x，函数的定义域为(0，＋∞)且f′(x)＝－＝，
令f′(x)＝0，得x＝2，
于是当x变化时，f′(x)，f(x)的变化情况如下表.
x
(0，2)
2
(2，＋∞)
f′(x)
＋
0
－
f(x)

ln 2－1

故f(x)在定义域上的极大值为f(x)极大值＝f(2)＝ln 2－1，无极小值.
(2)由(1)知，函数f(x)的定义域为(0，＋∞)，
f′(x)＝－a＝.
当a≤0时，f′(x)>0在(0，＋∞)上恒成立，
则函数在(0，＋∞)上单调递增，此时函数在定义域上无极值点；
当a>0时，若x∈，则f′(x)>0，
若x∈，则f′(x)<0，
故函数在x＝处有极大值.
综上可知，当a≤0时，函数f(x)无极值点，
当a>0时，函数y＝f(x)有一个极大值点，且为x＝.
感悟提升　运用导数求函数f(x)极值的一般步骤：(1)确定函数f(x)的定义域；(2)求导数f′(x)；(3)解方程f′(x)＝0，求出函数定义域内的所有根；(4)列表检验f′(x)在f′(x)＝0的根x0左右两侧值的符号；(5)求出极值.
角度3　由函数的极值求参数
例3 设函数g(x)＝ln x－mx＋，若g(x)存在两个极值点x1，x2，求实数m的取值范围.
解　∵g(x)＝ln x－mx＋，
∴g′(x)＝－m－＝
＝－，
令h(x)＝mx2－x＋m，要使g(x)存在两个极值点x1，x2，
则方程mx2－x＋m＝0有两个不相等的正数根x1，x2.
∵＞0，∴h(0)＝m＞0，
故只需满足即可，解得0＜m＜.
故m的取值范围为.
感悟提升　1.已知函数极值，确定函数解析式中的参数时，要注意：根据极值点的导数为0和极值这两个条件列方程组，利用待定系数法求解.
2.导数值为0不是此点为极值点的充要条件，所以用待定系数法求解后必须检验.
训练1 (1)设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是(　　)
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(－2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(－2)
D.函数f(x)有极大值f(－2)和极小值f(2)
答案　D
解析　由题图可知，当x<－2时，f′(x)>0；
当－2 当x>2时，f′(x)>0.
由此可以得到函数f(x)在x＝－2处取得极大值，
在x＝2处取得极小值.
(2)设函数f(x)＝，若f(x)在x＝－2处取得极大值，求a的取值范围.
解　因为f(x)＝，
所以f′(x)＝

＝－.
若a≠0，
令f′(x)＝0，则x＝或x＝－2，当＞－2时，即＞0，∴a＞0或a＜－1.
①若a＜－1时，
x
(－∞，－2)
－2



f′(x)
＋
0
－
0
＋
f(x)

极大值

极小值

此时，f(x)在x＝－2处取得极大值，符合题意.
②若a＞0时，当x＜－2或x＞时，f′(x)＜0，
当－2＜x＜时，f′(x)＞0，
∴f(x)在x＝2处取得极小值，不符合题意；
③若＜－2，即－1＜a＜0时，
当x＜或x＞－2时，f′(x)＞0，
当＜x＜－2时，f′(x)＜0，
∴f(x)在x＝－2处取得极小值，不符合题意；
④若＝－2，即a＝－1时，f′(x)≥0，f(x)无极值，不符合题意；
⑤若a＝0时，f′(x)＝，当x＜－2时，f′(x)＜0，
当x＞－2时，f′(x)＞0，∴f(x)在x＝－2处取得极小值，不符合题意.
综上，a的取值范围为(－∞，－1).
　考点二　利用导数求函数的最值
例4 (2021·北京卷)已知函数f(x)＝.
(1)若a＝0，求y＝f(x)在(1，f(1))处的切线方程；
(2)若函数f(x)在x＝－1处取得极值，求f(x)的单调区间，以及最大值和最小值.
解　(1)当a＝0时，f(x)＝，
则f′(x)＝
＝.
当x＝1时，f(1)＝1，f′(1)＝－4，
故y＝f(x)在(1，f(1))处的切线方程为
y－1＝－4(x－1)，
整理得4x＋y－5＝0.
(2)已知函数f(x)＝，
则f′(x)＝
＝.
若函数f(x)在x＝－1处取得极值，
则f′(－1)＝0，即＝0，解得a＝4.
经检验，当a＝4时，x＝－1为函数f(x)的极大值，符合题意.
此时f(x)＝，其定义域为R，f′(x)＝，
令f′(x)＝0，解得x1＝－1，x2＝4.
f(x)，f′(x)随x的变化趋势如下表：
x
(－∞，－1)
－1
(－1，4)
4
(4，＋∞)
f′(x)
＋
0
－
0
＋
f(x)
↗
极大值
↘
极小值
↗
故函数f(x)的单调递增区间为(－∞，－1)，(4，＋∞)，单调递减区间为(－1，4).
极大值为f(－1)＝1，极小值为f(4)＝－.
又因为x<时，f(x)>0；x>时，f(x)<0，
所以函数f(x)的最大值为f(－1)＝1，
最小值为f(4)＝－.
感悟提升　1.利用导数求函数f(x)在[a，b]上的最值的一般步骤：
(1)求函数在(a，b)内的极值.
(2)求函数在区间端点处的函数值f(a)，f(b).
(3)将函数f(x)的各极值与f(a)，f(b)比较，其中最大的一个为最大值，最小的一个为最小值.
2.求函数在无穷区间(或开区间)上的最值，不仅要研究其极值情况，还要研究其单调性，并通过单调性和极值情况，画出函数的大致图象，然后借助图象观察得到函数的最值.
训练2 已知函数f(x)＝ax＋ln x，其中a为常数.
(1)当a＝－1时，求f(x)的最大值；
(2)若f(x)在区间(0，e]上的最大值为－3，求a的值.
解　(1)易知f(x)的定义域为(0，＋∞)，
当a＝－1时，f(x)＝－x＋ln x，
f′(x)＝－1＋＝，
令f′(x)＝0，得x＝1.
当0＜x＜1时，f′(x)＞0；
当x＞1时，f′(x)＜0.
∴f(x)在(0，1)上单调递增，在(1，＋∞)上单调递减.
∴f(x)max＝f(1)＝－1.
∴当a＝－1时，函数f(x)在(0，＋∞)上的最大值为－1.
(2)f′(x)＝a＋，x∈(0，e]，
∈.
①若a≥－，则f′(x)≥0，从而f(x)在(0，e]上单调递增，
∴f(x)max＝f(e)＝ae＋1≥0，不符合题意.
②若a＜－，令f′(x)＞0得a＋＞0，结合x∈(0，e]，解得0＜x＜－；
令f′(x)＜0得a＋＜0，结合x∈(0，e]，解得－＜x≤e.
从而f(x)在上单调递增，
在上单调递减，
∴f(x)max＝f＝－1＋ln.
令－1＋ln＝－3，得ln＝－2，
即a＝－e2.
∵－e2＜－，∴a＝－e2为所求.
故实数a的值为－e2.


1.已知函数f(x)的定义域为(a，b)，导函数f′(x)在(a，b)上的图象如图所示，则函数f(x)在(a，b)上的极大值点的个数为(　　)
A.1 B.2 C.3 D.4
答案　B
解析　由函数极值的定义和导函数的图象可知，f′(x)在(a，b)上与x轴的交点个数为4，但是在原点附近的导数值恒大于零，故x＝0不是函数f(x)的极值点.其余的3个交点都是极值点，其中有2个点满足其附近的导数值左正右负，故极大值点有2个.
2.已知a为函数f(x)＝x3－12x的极小值点，则a等于(　　)
A.－4 B.－2 C.4 D.2
答案　D
解析　由题意得f′(x)＝3x2－12，由f′(x)＝0得x＝±2，当x∈(－∞，－2)时，f′(x)>0，函数f(x)单调递增，当x∈(－2，2)时，f′(x)<0，函数f(x)单调递减，当x∈(2，＋∞)时，f′(x)>0，函数f(x)单调递增，所以a＝2.
3.函数f(x)＝在[2，＋∞)上的最小值为(　　)
A. B.e2 C. D.2e
答案　A
解析　依题意f′(x)＝(x2－2x－3)
＝(x－3)(x＋1)，故函数在区间(2，3)上单调递减，在区间(3，＋∞)上单调递增，故函数在x＝3处取得极小值也即是最小值，且最小值为f(3)＝＝.

4.已知函数f(x)＝x3＋bx2＋cx的图象如图所示，则x＋x等于(　　)
A. B. C. D.
答案　C
解析　由题中图象可知f(x)的图象经过点(1，0)与(2，0)，x1，x2是函数f(x)的极值点，所以1＋b＋c＝0，8＋4b＋2c＝0，解得b＝－3，c＝2，所以f(x)＝x3－3x2＋2x，所以f′(x)＝3x2－6x＋2，x1，x2是方程3x2－6x＋2＝0的两根，所以x1＋x2＝2，x1·x2＝，∴x＋x＝(x1＋x2)2－2x1x2＝4－2×＝.
5.已知定义在R上的函数f(x)满足f(x＋4)＝－f(x)，函数f(x＋2)为偶函数，当x∈(0，2)时，f(x)＝－x3＋x2－6x＋a.若x∈(－2，0)时，f(x)的最大值为－，则a＝(　　)
A.3 B.2 C. D.－
答案　A
解析　由函数f(x＋2)是偶函数，得f(x)关于直线x＝2对称，即f(x＋4)＝f(－x)，因为f(x＋4)＝－f(x)，所以f(－x)＝－f(x)，故f(x)为奇函数，因为f(x)在(－2，0)上的最大值为－，所以f(x)在(0，2)上的最小值是，当x∈(0，2)时，f′(x)＝－3x2＋9x－6，令f′(x)＝0，得x＝1，故f(x)在(0，1)上单调递减，在(1，2)上单调递增，故x＝1时，f(x)取极小值，即最小值，故f(x)min＝f(1)＝a－＝，故a＝3.
6.(多选)(2022·烟台模拟)已知函数f(x)＝，则下列结论正确的是(　　)
A.函数f(x)存在两个不同的零点
B.函数f(x)既存在极大值又存在极小值
C.当－e＜k≤0时，方程f(x)＝k有且只有两个实根
D.若x∈[t，＋∞)时，f(x)max＝，则t的最小值为2
答案　ABC
解析　由f(x)＝0，得x2＋x－1＝0，
∴x＝，故A正确；
f′(x)＝－＝－，
当x∈(－∞，－1)∪(2，＋∞)时，f′(x)＜0，
当x∈(－1，2)时，f′(x)＞0，
∴f(x)在(－∞，－1)，(2，＋∞)上单调递减，在(－1，2)上单调递增，
∴f(－1)是函数的极小值，f(2)是函数的极大值，故B正确；
又f(－1)＝－e，f(2)＝，
且当x→－∞时，f(x)→＋∞，x→＋∞时，f(x)→0，
∴f(x)的图象如图所示，

由图知C正确，D不正确.
7.若商品的年利润y(万元)与年产量x(百万件)的函数关系式为y＝－x3＋27x＋123(x>0)，则获得最大利润时的年产量为________百万件.
答案　3
解析　y′＝－3x2＋27＝－3(x＋3)(x－3)，当00；当x>3时，y′<0.
故当x＝3时，该商品的年利润最大.
8.(2022·安徽江南十校联考)已知x＝1是函数f(x)＝(x2＋ax)ex的一个极值点，则曲线y＝f(x)在点(0，f(0))处的切线斜率为________.
答案　－
解析　由f(x)＝(x2＋ax)ex，
得f′(x)＝(x2＋ax＋2x＋a)ex，
因为x＝1是函数f(x)＝(x2＋ax)ex的一个极值点，
所以f′(1)＝(3＋2a)e＝0，解得a＝－.
∴f′(x)＝ex，
所以f′(0)＝－.
所以曲线f(x)在点(0，f(0))处的切线斜率为－.
9.(2021·新高考Ⅰ卷)函数f(x)＝|2x－1|－2ln x的最小值为________.
答案　1
解析　函数f(x)＝|2x－1|－2ln x的定义域为(0，＋∞).
①当x>时，f(x)＝2x－1－2ln x，
所以f′(x)＝2－＝.
当1时，f′(x)>0，所以f(x)在上单调递减，在(1，＋∞)上单调递增，所以f(x)min＝f(1)＝2－1－2ln 1＝1；
②当0ln e＝1.
综上，f(x)min＝1.
10.已知函数f(x)＝excos x－x.
(1)求曲线y＝f(x)在点(0，f(0))处的切线方程；
(2)求函数f(x)在区间上的最大值和最小值.
解　(1)因为f(x)＝excos x－x，
所以f′(x)＝ex(cos x－sin x)－1，f′(0)＝0.
又因为f(0)＝1，
所以曲线y＝f(x)在点(0，f(0))处的切线方程为y＝1.
(2)设h(x)＝ex(cos x－sin x)－1，
则h′(x)＝ex(cos x－sin x－sin x－cos x)＝－2exsin x.
当x∈时，h′(x)<0，
所以h(x)在区间上单调递减，
所以对任意x∈有h(x) 所以函数f(x)在区间上单调递减.
因此f(x)在区间上的最大值为f(0)＝1，最小值为f＝－.
11.设函数f(x)＝(x－a)(x－b)(x－c)，a，b，c∈R，f′(x)为f(x)的导函数.
(1)若a＝b＝c，f(4)＝8，求a的值；
(2)若a≠b，b＝c，且f(x)和f′(x)的零点均在集合{－3，1，3}中，求f(x)的极小值.
解　(1)因为a＝b＝c，
所以f(x)＝(x－a)(x－b)(x－c)＝(x－a)3.
因为f(4)＝8，所以(4－a)3＝8，解得a＝2.
(2)因为b＝c，所以f(x)＝(x－a)(x－b)2＝x3－(a＋2b)x2＋b(2a＋b)x－ab2，从而f′(x)＝3(x－b)·.
令f′(x)＝0，得x＝b或x＝.
令f(x)＝0，得x＝a或x＝b.
因为a，b，都在集合{－3，1，3}中，
且a≠b，
所以＝1，a＝3，b＝－3.
此时，f(x)＝(x－3)(x＋3)2，f′(x)＝3(x＋3)(x－1).
令f′(x)＝0，得x＝－3或x＝1.
当x变化时，f′(x)变化如下表：
x
(－∞，－3)
－3
(－3，1)
1
(1，＋∞)
f′(x)
＋
0
－
0
＋
f(x)

极大值

极小值

所以f(x)的极小值为f(1)＝(1－3)(1＋3)2＝－32.

12.(多选)(2022·青岛模拟)对于函数f(x)＝16ln(1＋x)＋x2－10x，下列说法正确的是(　　)
A.x＝3是函数f(x)的一个极值点
B.f(x)的单调递增区间是(－1，1)，(2，＋∞)
C.f(x)在区间(1，2)上单调递减
D.直线y＝16ln 3－16与函数f(x)的图象有3个交点
答案　ACD
解析　由题意得f′(x)＝＋2x－10＝，x＞－1，令2x2－8x＋6＝0，得x＝1或x＝3，则f(x)在(－1，1)，(3，＋∞)上单调递增，在(1，3)上单调递减，所以x＝3是函数f(x)的一个极值点，故A、C正确，B错误.f(1)＝16ln(1＋1)＋12－10＝16ln 2－9，f(3)＝16ln(1＋3)＋32－10×3＝16ln 4－21，且y＝16ln 3－16＝f(2)，根据f(x)在(1，3)上单调递减得f(1)＞f(2)＞f(3)，又x→－1时，f(x)→－∞，x→＋∞时，f(x)→＋∞，所以直线y＝16ln 3－16与函数f(x)的图象有3个交点，故D正确.
13.已知函数f(x)＝xln x＋mex(e为自然对数的底数)有两个极值点，则实数m的取值范围是________.
答案　
解析　f(x)＝xln x＋mex(x＞0)，
∴f′(x)＝ln x＋1＋mex(x＞0)，
令f′(x)＝0，得－m＝，
设g(x)＝，
则g′(x)＝(x＞0)，
令h(x)＝－ln x－1，
则h′(x)＝－－＜0(x＞0)，
∴h(x)在(0，＋∞)上单调递减且h(1)＝0，
∴当x∈(0，1]时，h(x)≥0，即g′(x)≥0，g(x)在(0，1]上单调递增；
当x∈(1，＋∞)时，h(x)＜0，即g′(x)＜0，g(x)在(1，＋∞)上单调递减，
故g(x)max＝g(1)＝，
而当x→0时，g(x)→－∞，当x→＋∞时，g(x)→0，
若f(x)有两极值点，只要y＝－m和g(x)的图象在(0，＋∞)上有两个交点，
只需0＜－m＜，故－＜m＜0.
14.已知函数f(x)＝x3－ax2，a∈R.
(1)当a＝2时，求曲线y＝f(x)在点(3，f(3))处的切线方程；
(2)设函数g(x)＝f(x)＋(x－a)cos x－sin x，讨论g(x)的单调性并判断有无极值，有极值时求出极值.
解　(1)由题意f′(x)＝x2－ax，
所以当a＝2时，f(3)＝0，f′(x)＝x2－2x，
所以f′(3)＝3，
因此曲线y＝f(x)在点(3，f(3))处的切线方程是y＝3(x－3)，即3x－y－9＝0.
(2)因为g(x)＝f(x)＋(x－a)cos x－sin x，
所以g′(x)＝f′(x)＋cos x－(x－a)sin x－cos x＝x(x－a)－(x－a)sin x
＝(x－a)(x－sin x)，
令h(x)＝x－sin x，
则h′(x)＝1－cos x≥0，
所以h(x)在R上单调递增.
因为h(0)＝0，所以，当x>0时，h(x)>0；
当x<0时，h(x)<0.
①当a<0时，g′(x)＝(x－a)(x－sin x)，
当x∈(－∞，a)时，x－a<0，g′(x)>0，g(x)单调递增；
当x∈(a，0)时，x－a>0，g′(x)<0，g(x)单调递减；
当x∈(0，＋∞)时，x－a>0，g′(x)>0，g(x)单调递增.
所以，当x＝a时，g(x)取到极大值，
极大值是g(a)＝－a3－sin a，
当x＝0时，g(x)取到极小值，极小值是g(0)＝－a.
②当a＝0时，g′(x)＝x(x－sin x)，
当x∈(－∞，＋∞)时，g′(x)≥0，g(x)单调递增；
所以g(x)在(－∞，＋∞)上单调递增，g(x)无极大值也无极小值.
③当a>0时，g′(x)＝(x－a)(x－sin x)，
当x∈(－∞，0)时，x－a<0，g′(x)>0，g(x)单调递增；
当x∈(0，a)时，x－a<0，g′(x)<0，g(x)单调递减；
当x∈(a，＋∞)时，x－a>0，g′(x)>0，g(x)单调递增.
所以，当x＝0时，g(x)取到极大值，
极大值是g(0)＝－a；
当x＝a时g(x)取到极小值，
极小值是g(a)＝－a3－sin a.
综上所述：
当a<0时，函数g(x)在(－∞，a)和(0，＋∞)上单调递增，在(a，0)上单调递减，函数既有极大值，又有极小值，极大值是g(a)＝－a3－sin a，极小值是g(0)＝－a；
当a＝0时，函数g(x)在(－∞，＋∞)上单调递增，无极值；
当a>0时，函数g(x)在(－∞，0)和(a，＋∞)上单调递增，在(0，a)上单调递减，函数既有极大值，又有极小值，极大值是g(0)＝－a，极小值是g(a)＝－a3－sin a.