

广东省广州市黄埔区会元学校2021-2022学年八年级上学期期中数学【试卷+答案】
展开2021-2022学年广东省广州市黄埔区会元学校八年级第一学期期中数学试卷
一、单选题(本题有10个小题,每小题3分,满分30分,每小题给出的四个选项中,只有一个是正确的。)
1.下列四个图标中,是轴对称图形的是( )
A. B. C. D.
2.下列各组线段中,能构成三角形的是( )
A.1,1,3 B.2,3,5 C.3,4,9 D.5,6,10
3.下列运算正确的是( )
A.a3+a3=a6 B.(a3)2=a6
C.(ab)2=ab2 D.2a5•3a5=5a5
4.如图所示,∠1=∠2=145°,则∠3=( )
A.80° B.70° C.60° D.50°
5.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△MOC≌△NOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
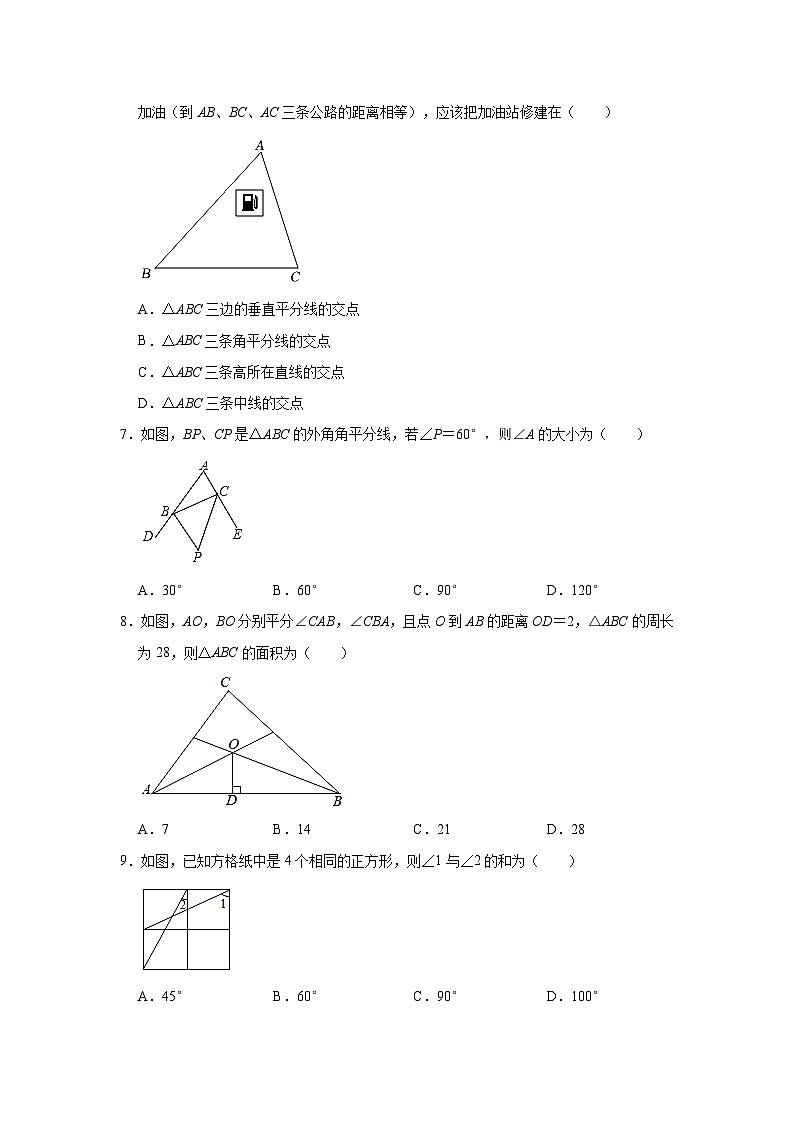
6.如图,地面上有三条公路AB,BC,AC,要想在修建一个加油站方便三条公路上的车辆加油(到AB、BC、AC三条公路的距离相等),应该把加油站修建在( )
A.△ABC三边的垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
7.如图,BP、CP是△ABC的外角角平分线,若∠P=60°,则∠A的大小为( )
A.30° B.60° C.90° D.120°
8.如图,AO,BO分别平分∠CAB,∠CBA,且点O到AB的距离OD=2,△ABC的周长为28,则△ABC的面积为( )
A.7 B.14 C.21 D.28
9.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )
A.45° B.60° C.90° D.100°
10.如图,已知△ABC中,AB=AC=24cm,∠B=∠C,BC=16cm,点D为AB的中点,如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为( )cm/s时,能够在某一时刻使△BPD与△CQP全等.
A.4 B.3 C.4或3 D.4或6
二、填空题(本题有6个小题,每小题3分,共18分)
11.点P(﹣1,2)关于x轴对称点P1的坐标为 .
12.如图,点A、E、B、F在同一条直线上,AC∥DF,AC=DF,要使△ABC≌△FED,则可以补充一个条件: .
14.已知等腰三角形的一个外角是70°,则它顶角的度数为 .
15.如图,在Rt△ABC中,∠C=90°,∠B=60°,点D在边AC上,DE⊥AB,垂足为点E,且BE=BC.若AD=6cm,则CD的长为 cm.
16.如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为 .(填写序号)
三、解答题(本题有9个小题,共72分,解答要求写出文字说明,证明过程或计算步骤)
17.计算:
(1)(﹣3x3)2﹣x2•x4﹣(x2)3.
(2)已知ax=﹣2,ay=3.求a2x+y的值.
18.如图,已知OA=OC,OB=OD,∠1=∠2,求证:AB=CD.
19.如图,AB=AC,AB的垂直平分线交AB于E,交AC于D.
(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长17,求△ABC的周长.
20.如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△A1B1C1,使它与△ABC关于直线l对称;
(2)在直线l上找一点P,使得PA+PC最小;
(3)△ABC的面积为 .
21.如图,在△ABC中,∠C=90°.
(1)作△ABC的角平分线AD.(要求:尺规作图,保留作图痕迹,不写作法);
(2)若AB=10,CD=3,则△ABD的面积等于 .
22.如图,在△ABC中,AE是BC边上的高.
(1)若AD是边BC上的中线,AE=3cm,S△ABC=6cm²,求DC的长;
(2)若AD是∠BAC的平分线,∠C﹣∠B=30°,求∠DAE的度数.
23.如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D
(1)求证:AC=CB;
(2)若AC=12cm,求BD的长.
24.如图1,D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)求证:△ADE是等边三角形;
(2)如图2,DE交CB于点P,若DE⊥AC,PC=4,求BP的长.
25.在平面直角坐标系中,点A的坐标为(8,0),点B为y轴正半轴上的一个动点,以B为直角顶点,AB为直角边在第一象限作等腰Rt△ABC.
(1)如图1,若OB=6,则点C的坐标为 ;
(2)如图2,若OB=8,点D为OA延长线上一点,以D为直角顶点,BD为直角边在第一象限作等腰Rt△BDE,连接AE,求证:AE⊥AB;
(3)如图3,以B为直角顶点,OB为直角边在第三象限作等腰Rt△OBF,连接CF,交y轴于点P,求线段BP的长.
参考答案
一、单选题(本题有10个小题,每小题3分,满分30分,每小题给出的四个选项中,只有一个是正确的。)
1.下列四个图标中,是轴对称图形的是( )
A. B. C. D.
【分析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,直接根据轴对称图形的概念即可得出答案.
解:A、不是轴对称图形,不合题意;
B、不是轴对称图形,不合题意;
C、是轴对称图形,符合题意;
D、不是轴对称图形,不合题意.
故选:C.
2.下列各组线段中,能构成三角形的是( )
A.1,1,3 B.2,3,5 C.3,4,9 D.5,6,10
【分析】由于三角形三边满足两短边的和大于最长的边,只要不满足这个关系就不能构成三角形.根据这个关系即可确定选择项.
解:A、∵1+1=2<3,
∴无法构成三角形,不合题意;
B、∵2+3=5,
∴无法构成三角形,不合题意;
C、∵3+4=7<9,
∴无法构成三角形,不合题意;
D、∵5+6=11>10,
∴可以构成三角形,符合题意;
故选:D.
3.下列运算正确的是( )
A.a3+a3=a6 B.(a3)2=a6
C.(ab)2=ab2 D.2a5•3a5=5a5
【分析】利用合并同类项的法则,幂的乘方与积的乘方的法则,单项式乘单项式的法则对各项进行运算即可.
解:A、a3+a3=2a3,故A不符合题意;
B、(a3)2=a6,故B符合题意;
C、(ab)2=a2b2,故C不符合题意;
D、2a5•3a5=6a10,故D不符合题意;
故选:B.
4.如图所示,∠1=∠2=145°,则∠3=( )
A.80° B.70° C.60° D.50°
【分析】根据三角形的外角和等于360°计算即可.
解:∵∠1、∠2、∠3是△ABC的三个外角,
∴∠1+∠2+∠3=360°,
∵∠1=∠2=145°,
∴∠3=360°﹣145°×2=70°,
故选:B.
5.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△MOC≌△NOC,其依据是( )
A.SSS B.SAS C.ASA D.AAS
【分析】由作图过程可得MO=NO,NC=MC,再加上公共边CO=CO可利用SSS定理判定△MOC≌△NOC.
解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
6.如图,地面上有三条公路AB,BC,AC,要想在修建一个加油站方便三条公路上的车辆加油(到AB、BC、AC三条公路的距离相等),应该把加油站修建在( )
A.△ABC三边的垂直平分线的交点
B.△ABC三条角平分线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条中线的交点
【分析】根据角平分线性质,同时加油站的位置到三条路距离相等,从而得到加油站修建在△ABC三条角平分线的交点处.
解:三角形中到三边的距离相等的是三角形的内心,即为三条内角平分线的交点.
故选:B.
7.如图,BP、CP是△ABC的外角角平分线,若∠P=60°,则∠A的大小为( )
A.30° B.60° C.90° D.120°
【分析】利用三角形的外角的性质以及三角形的内角和定理解决问题即可.
【解答】证明:∵BP、CP是△ABC的外角的平分线,
∴∠PCB=∠ECB,∠PBC=∠DBC,
∵∠ECB=∠A+∠ABC,∠DBC=∠A+∠ACB,
∴∠PCB+∠PBC=(∠A+∠ABC+∠A+∠ACB)=(180°+∠A)=90°+∠A,
∴∠P=180°﹣(∠PCB+∠PBC)=180°﹣(90°+∠A)=90°﹣∠A=60°,
∴∠A=60°,
故选:B.
8.如图,AO,BO分别平分∠CAB,∠CBA,且点O到AB的距离OD=2,△ABC的周长为28,则△ABC的面积为( )
A.7 B.14 C.21 D.28
【分析】连接OC,过点O作OE⊥AC于E,OF⊥BC于F,根据角平分线的性质得到OE=OF=OD=2,根据三角形的面积公式计算,得到答案.
解:连接OC,过点O作OE⊥AC于E,OF⊥BC于F,
∵AO,BO分别平分∠CAB,∠CBA,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OF=OD=2,
∴△ABC的面积=△AOC的面积+△AOB的面积+△BOC的面积
=×AC×OE+×AB×OD+×BC×OF
=×(AB+AC+BC)×2
=28.
故选:D.
9.如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为( )
A.45° B.60° C.90° D.100°
【分析】首先证明△ABC≌△DFE,根据全等三角形的性质可得∠1=∠BAC,再根据余角的定义可得∠BAC+∠2=90°,再根据等量代换可得∠1与∠2的和为90°.
解:在△ABC和△DFE中,
,
∴△ABC≌△DFE(SAS),
∴∠1=∠BAC,
∵∠BAC+∠2=90°,
∴∠1+∠2=90°,
故选:C.
10.如图,已知△ABC中,AB=AC=24cm,∠B=∠C,BC=16cm,点D为AB的中点,如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动,当点Q的运动速度为( )cm/s时,能够在某一时刻使△BPD与△CQP全等.
A.4 B.3 C.4或3 D.4或6
【分析】根据等边对等角可得∠B=∠C,然后表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD与CQ是对应边两种情况讨论求解即可.
解:∵AB=24cm,BC=16cm,点D为AB的中点,
∴BD=×24=12cm,
设点P、Q的运动时间为ts,
∴BP=4t,
∴PC=(16﹣4t)cm
①当BD=PC时,16﹣4t=12,
解得:t=1,
则BP=CQ=4,
故点Q的运动速度为:4÷1=4(cm/s);
②当BP=PC时,
∵BC=16cm,
∴BP=PC=8cm,
∴t=8÷4=2.
故点Q的运动速度为12÷2=6(cm/s).
故选:D.
二、填空题(本题有6个小题,每小题3分,共18分)
11.点P(﹣1,2)关于x轴对称点P1的坐标为 (﹣1,﹣2) .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
解:点P(﹣1,2)关于x轴对称点P1的坐标为(﹣1,﹣2),
故答案为:(﹣1,﹣2).
12.如图,点A、E、B、F在同一条直线上,AC∥DF,AC=DF,要使△ABC≌△FED,则可以补充一个条件: AB=EF .
【分析】根据平行线的性质,由AC∥DF,得∠A=∠F,从而解决此题.
解:补充条件:AB=EF.
∵AC∥DF,
∴∠A=∠F.
在△ABC和△FED中,
,
∴△ABC≌△FED(SAS).
故答案为:AB=EF.
14.已知等腰三角形的一个外角是70°,则它顶角的度数为 110° .
【分析】三角形内角与相邻的外角和为180°,三角形内角和为180°,等腰三角形两底角相等,110°只可能是顶角.
解:等腰三角形一个外角为70°,那相邻的内角为110°,
三角形内角和为180°,如果这个内角为底角,内角和将超过180°,
所以110°只可能是顶角.
故答案为:110°.
15.如图,在Rt△ABC中,∠C=90°,∠B=60°,点D在边AC上,DE⊥AB,垂足为点E,且BE=BC.若AD=6cm,则CD的长为 3 cm.
【分析】连接BD,根据HL证明Rt△BCD与Rt△BED全等,进而利用全等三角形的性质和含30°角的直角三角形的性质解答即可.
解:连接BD,
在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴CD=DE,
在Rt△ADE中,∠A=90°﹣60°=30°,AD=6cm,
∴DE=3cm,
∴CD=3cm,
故答案为:3.
16.如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为 ①②④⑤ .(填写序号)
【分析】由三角形内角和定理和角平分线得出∠PBC+∠PCB的度数,再由三角形内角和定理可求出∠BPC的度数,①正确;由∠BPC=120°可知∠DPE=120°,过点P作PF⊥AB,PG⊥AC,PH⊥BC,由角平分线的性质可知AP是∠BAC的平分线,②正确;PF=PG=PH,故∠AFP=∠AGP=90°,由四边形内角和定理可得出∠FPG=120°,故∠DPF=∠EPG,由全等三角形的判定定理可得出△PFD≌△PGE,故可得出PD=PE,④正确;由三角形全等的判定定理可得出△BHP≌△BFP,△CHP≌△CGP,故可得出BH=BD+DF,CH=CE﹣GE,再由DF=EG可得出BC=BD+CE,⑤正确;即可得出结论.
解:∵BE、CD分别是∠ABC与∠ACB的角平分线,∠BAC=60°,
∴∠PBC+∠PCB=(180°﹣∠BAC)=(180°﹣60°)=60°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣60°=120°,①正确;
∵∠BPC=120°,
∴∠DPE=120°,
过点P作PF⊥AB,PG⊥AC,PH⊥BC,
∵BE、CD分别是∠ABC与∠ACB的角平分线,
∴AP是∠BAC的平分线,②正确;
∴PF=PG=PH,
∵∠BAC=60°∠AFP=∠AGP=90°,
∴∠FPG=120°,
∴∠DPF=∠EPG,
在△PFD与△PGE中,,
∴△PFD≌△PGE(ASA),
∴PD=PE,④正确;
在Rt△BHP与Rt△BFP中,,
∴Rt△BHP≌Rt△BFP(HL),
同理,Rt△CHP≌Rt△CGP,
∴BH=BD+DF,CH=CE﹣GE,
两式相加得,BH+CH=BD+DF+CE﹣GE,
∵DF=EG,
∴BC=BD+CE,⑤正确;
没有条件得出AD=AE,③不正确;
故答案为:①②④⑤.
三、解答题(本题有9个小题,共72分,解答要求写出文字说明,证明过程或计算步骤)
17.计算:
(1)(﹣3x3)2﹣x2•x4﹣(x2)3.
(2)已知ax=﹣2,ay=3.求a2x+y的值.
【分析】(1)先进行积的乘方与幂的乘方的运算,同底数幂的乘法运算,再合并同类项即可;
(2)利用同底数幂的乘法与幂的乘方对所求的式子进行整理,再代入相应的值运算即可.
解:(1)(﹣3x3)2﹣x2•x4﹣(x2)3
=9x6﹣x6﹣x6
=7x6.
(2)∵ax=﹣2,ay=3,
∴a2x+y
=a2x×ay
=(ax)2×ay
=(﹣2)2×3
=4×3
=12.
18.如图,已知OA=OC,OB=OD,∠1=∠2,求证:AB=CD.
【分析】由∠1=∠2知∠AOB=∠COD,再结合OA=OC、OB=OD,利用“SAS”判定△AOB≌△COD,根据全等三角形的性质即可得证.
【解答】证明:∵∠1=∠2,
∴∠1+∠AOD=∠2+∠AOD,即∠AOB=∠COD,
在△AOB和△COD中,
∵,
∴△AOB≌△COD(SAS),
∴AB=CD.
19.如图,AB=AC,AB的垂直平分线交AB于E,交AC于D.
(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长17,求△ABC的周长.
【分析】(1)根据等腰三角形的性质和三角形内角和等于180°列式求出∠BCD的度数;
(2)根据线段垂直平分线的性质可得AD=BD,AB=2AE,把△BCD的周长转化为AC、BC的和,然后代入数据进行计算即可得解.
解:(1)∵AB=AC,∠A=40°,
∴∠BCD=(180°﹣∠A)=(180°﹣40°)=70°;
(2)∵DE是AB的垂直平分线,
∴AD=BD,AB=2AE=10,
∵△BCD的周长=BD+CD+BC=AD+CD+BC=AC+BC=17,
∴△ABC的周长=10+17=27.
20.如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中画出△A1B1C1,使它与△ABC关于直线l对称;
(2)在直线l上找一点P,使得PA+PC最小;
(3)△ABC的面积为 5 .
【分析】(1)分别作出点A,B,C关于y轴的对称点,再顺次连接即可得;
(2)连接AC1,与直线l的交点即为所求;
(3)利用割补法求解可得.
解:(1)如图所示,△A1B1C1即为所求.
(2)连接AC1,则AC1与l的交点P即为所求的点.
(3)△ABC的面积为3×4﹣×1×4﹣×2×2﹣×2×3=5,
故答案为:5.
21.如图,在△ABC中,∠C=90°.
(1)作△ABC的角平分线AD.(要求:尺规作图,保留作图痕迹,不写作法);
(2)若AB=10,CD=3,则△ABD的面积等于 15 .
【分析】(1)利用基本作图,作∠BAC的平分线即可;
(2)过D点作DE⊥AB于E,如图,根据角平分线的性质得到DE=DC=3,然后根据三角形面积公式计算.
解:(1)如图,线段AD为所求;
(2)过D点作DE⊥AB于E,如图,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC=3,
∴S△ABD=×3×10=15.
故答案为15.
22.如图,在△ABC中,AE是BC边上的高.
(1)若AD是边BC上的中线,AE=3cm,S△ABC=6cm²,求DC的长;
(2)若AD是∠BAC的平分线,∠C﹣∠B=30°,求∠DAE的度数.
【分析】(1)根据三角形的面积公式,得=6,得BC=4.由AD是边BC上的中线,得CD==2(cm).
(2)设∠B=x,则∠C=x+30°.根据三角形内角和定理,得∠BAC=180°﹣∠B﹣∠C=150°﹣2x.由AD是∠BAC的平分线,得∠BAD==75°﹣x,那么∠ADE=∠B+∠BAD=x+75°﹣x=75°.由AE是BC边上的高,得∠AED=90°,那么∠DAE=180°﹣(∠ADE+∠DEA)=15°.
解:(1)∵=6,
∴×3=6.
∴BC=4.
∵AD是边BC上的中线,
∴CD==2(cm).
(2)设∠B=x,则∠C=x+30°.
∴∠BAC=180°﹣∠B﹣∠C=180°﹣x﹣(x+30°)=150°﹣2x.
∵AD是∠BAC的平分线,
∴∠BAD==75°﹣x.
∴∠ADE=∠B+∠BAD=x+75°﹣x=75°.
∵AE是BC边上的高,
∴∠AED=90°.
∴∠DAE=180°﹣(∠ADE+∠DEA)=180°﹣(75°+90°)=15°.
23.如图,△ABC中,∠ACB=90°,DC=AE,AE是BC边上的中线,过点C作CF⊥AE,垂足为点F,过点B作BD⊥BC交CF的延长线于点D
(1)求证:AC=CB;
(2)若AC=12cm,求BD的长.
【分析】(1)由“AAS”可证△DBC≌△ECA,可得AC=BC;
(2)由全等三角形的性质和中线的性质可求解.
【解答】证明:(1)∵DB⊥BC,AE⊥CD,
∴∠DBC=∠ACE=∠AFC=90°,
∵∠DCB+∠ACF=90°,∠ACF+∠EAC=90°,
∴∠DCB=∠EAC,且DC=AE,∠DBC=∠ACE=90°
∴△DBC≌△ECA(AAS)
∴AC=BC
(2)∵AE是BC边上的中线,
∴CE=BE=BC=AC=6cm,
∵△DBC≌△ECA
∴DB=CE=6cm
24.如图1,D为等边△ABC的边AC上一点,E为直线AB上一点,CD=BE.
(1)求证:△ADE是等边三角形;
(2)如图2,DE交CB于点P,若DE⊥AC,PC=4,求BP的长.
【分析】(1)只要证明△ADE是等边三角形即可;
(2)过点D作DQ∥AB,交BC于点Q,证△DQP≌△EBP(AAS),得QP=BP,再利用含30°角的直角三角形的性质即可解决问题.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵CD=BE,
∴AB﹣BE=AC﹣CD,
即AD=AE,
∵∠A=60°,
∴△ADE是等边三角形
(2)解:过点D作DQ∥AB,交BC于点Q,如图2所示:
则∠CDQ=∠A=60°,∠CQD=∠ABC=60°,∠DQP=∠EBP,
∴△DCQ是等边三角形,
∴DQ=CQ=CD=BE.
∵∠DPQ=∠EPB,∠DQP=∠EBP,
∴△DQP≌△EBP(AAS),
∴QP=BP,
∵DE⊥AC,
∴∠CDP=90°,
∵△ABC是等边三角形,
∴∠C=60°,
∴∠CPD=30°,
∴CQ=CD=PC=2,
∴QP=PC﹣CQ=2,
∴BP=QP=2.
25.在平面直角坐标系中,点A的坐标为(8,0),点B为y轴正半轴上的一个动点,以B为直角顶点,AB为直角边在第一象限作等腰Rt△ABC.
(1)如图1,若OB=6,则点C的坐标为 (6,14) ;
(2)如图2,若OB=8,点D为OA延长线上一点,以D为直角顶点,BD为直角边在第一象限作等腰Rt△BDE,连接AE,求证:AE⊥AB;
(3)如图3,以B为直角顶点,OB为直角边在第三象限作等腰Rt△OBF,连接CF,交y轴于点P,求线段BP的长.
【分析】(1)如图1,过点C作CH⊥y轴,由“AAS”可证△ABO≌△BCH,可得CH=OB=6,BH=AO=8,可求解;
(2)过点E作EF⊥x轴于F,由“AAS”可证△ABO≌△BCH,可得BO=DF=8,OD=EF,由等腰直角三角形的性质可得∠BAO=45°,∠EAF=∠AEF=45°,可得结论;
(3)由(1)可知△ABO≌△BCG,可得BO=GC,AO=BG=4,再由“AAS”可证△CPG≌△FPB,可得PB=PG=4.
解:(1)如图1,过点C作CH⊥y轴于H,
∴∠CHB=∠ABC=∠AOB=90°,
∴∠BCH+∠HBC=90°=∠HBC+∠ABO,
∴∠ABO=∠BCH,
在△ABO和△BCH中,
,
∴△ABO≌△BCH(AAS),
∴CH=OB=6,BH=AO=8,
∴OH=14,
∴点C(6,14),
故答案为:(6,14);
(2)过点E作EF⊥x轴于F,
∴∠EFD=∠BDE=∠BOD=90°,
∴∠BDO+∠EDF=90°=∠BDO+∠DBO,
∴∠DBO=∠EDF,
在△BOD和△DFE中,
,
∴△BOD≌△DFE(AAS),
∴BO=DF=8,OD=EF,
∵点A的坐标为(8,0),
∴OA=OB=8,
∴∠BAO=45°,
∵OA=DF=8,
∴OD=AF=EF,
∴∠EAF=∠AEF=45°,
∴∠BAE=90°,
∴BA⊥AE;
(3)过点C作CG⊥y轴G,
由(1)可知:△ABO≌△BCG,
∴BO=GC,AO=BG=8,
∵BF=BO,∠OBF=90°,
∴BF=GC,∠CGP=∠FBP=90°,
又∵∠CPG=∠FPB,
∴△CPG≌△FPB(AAS),
∴BP=GP,
∴BP=BG=4.
2023-2024学年广东省广州市黄埔区天键学校九年级(上)期中数学试卷(含解析): 这是一份2023-2024学年广东省广州市黄埔区天键学校九年级(上)期中数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
广东省广州市黄埔区天健学校2023-2024学年九年级上学期数学期中试卷: 这是一份广东省广州市黄埔区天健学校2023-2024学年九年级上学期数学期中试卷,共5页。试卷主要包含了之间,对称轴是直线x=1等内容,欢迎下载使用。
广东省广州市黄埔区天键学校2023—2024学年九年级上学期数学期中试卷: 这是一份广东省广州市黄埔区天键学校2023—2024学年九年级上学期数学期中试卷,共6页。












