


西藏拉萨市名校2022-2023学年数学七下期末达标检测试题含答案
展开西藏拉萨市名校2022-2023学年数学七下期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.点![]() 在第
在第![]()
![]() 象限.
象限.
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.如图,△ABC中,D,E分别是AB,AC的中点,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为( )
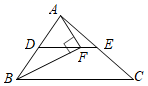
A.2.5 B.2 C.1.5 D.1
3.若x2+mxy+y2是一个完全平方式,则m=( )
A.2 B.1 C.±1 D.±2
4.已知x,y满足![]() ,则以x,y的值为两边长的等腰三角形的周长是( )
,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16 B.20 C.16 D.以上答案都不对
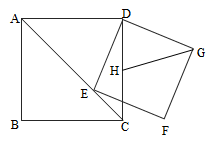
5.如图,在正方形![]() 中,
中,![]() ,
,![]() 是对角线
是对角线![]() 上的动点,以
上的动点,以![]() 为边作正方形
为边作正方形![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
6.若![]() ,则代数式
,则代数式![]() 的值是( )
的值是( )
A.9 B.7 C.![]() D.1
D.1
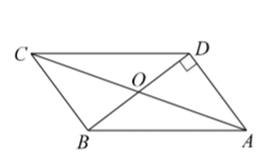
7.如图:点E、F为线段BD的两个三等分点,四边形AECF是菱形,且菱形AECF的周长为20,BD为24,则四边形ABCD的面积为( )
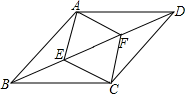
A.24 B.36 C.72 D.144
8.20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x人,女生有y人,根据题意,列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.在如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
![]()
A.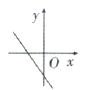 B.
B.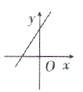 C.
C.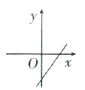 D.
D.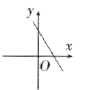
10.某次知识竞赛共有![]() 道题,每一题答对得
道题,每一题答对得![]() 分,答错或不答扣
分,答错或不答扣![]() 分,小亮得分要超过
分,小亮得分要超过![]() 分,他至少要答对多少道题?如果设小亮答对了
分,他至少要答对多少道题?如果设小亮答对了![]() 道题,根据题意列式得( )
道题,根据题意列式得( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.已知点![]() 在反比例函数
在反比例函数![]() 的图象上,则下列点也在该函数图象上的是( )
的图象上,则下列点也在该函数图象上的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知甲,乙两组数据的折线图如图所示,设甲,乙两组数据的方差分别为![]() ,
,![]() ,则
,则![]() 与
与![]() 大小关系为( )
大小关系为( )
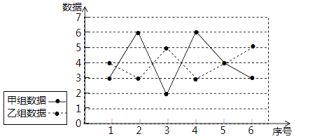
A.![]() B.
B.![]()
C.![]() D.不能确定
D.不能确定
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.如图,在平行四边形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,且
,且![]() .已知
.已知![]() ,则
,则![]() ____.
____.
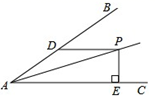
14.若∠BAC=30°,AP平分∠BAC,PD∥AC,且PD=6,PE⊥AC,则PE=________.
15.若分式![]() 的值为0,则
的值为0,则![]() __.
__.
16.据说,我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口而出:1.你知道他是怎么快速准确地计算出来的吗?请研究解决下列问题:
已知x3=10648,且x为整数
∵1000=103<10648<1003=1000000,
∴x一定是______位数
∵10648的个位数字是8,
∴x的个位数字一定是______;
划去10648后面的三位648得10,
∵8=23<10<33=27,
∴x的十位数字一定是_____;
∴x=______.
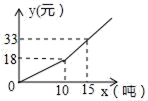
17.我国很多城市水资源短缺,为了加强居民的节水意识,某自来水公司采取分段收费标准.某市居民月交水费y(单位:元)与用水量x(单位:吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费_____元.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)某社区计划对面积为1200m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)甲、乙两施工队每天分别能完成绿化的面积是多少?
(2)设先由甲队施工x天,再由乙队施工y天,刚好完成绿化任务,求y与x的函数解析式;
(3)在(2)的情况下,若甲队绿化费用为1600元/天,乙队绿化费用为700元/天,在施工过程中每天需要支付高温补贴a元(100≤a≤300),且工期不得超过14天,则如何安排甲,乙两队施工的天数,使施工费用最少?
19.(5分)某校七、八年级各有学生400人,为了解这两个年级普及安全教育的情况,进行了抽样调查,过程如下
选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下:
七年级 85 79 89 83 89 98 68 89 79 59
99 87 85 89 97 86 89 90 89 77
八年级 71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
分组整理,描述数据
(1)按如下频数分布直方图整理、描述这两组样本数据,请补全八年级20名学生安全教育频数分布直方图;
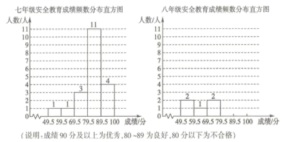
(2)两组样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
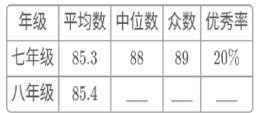
得出结论,说明理由.
(3)整体成绩较好的年级为___,理由为___(至少从两个不同的角度说明合理性).
20.(8分)如图,![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,
,![]() .
.
求证:![]() ≌
≌![]()
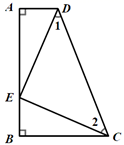
21.(10分)如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
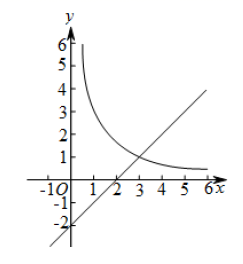
22.(10分)为了解某中学学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:
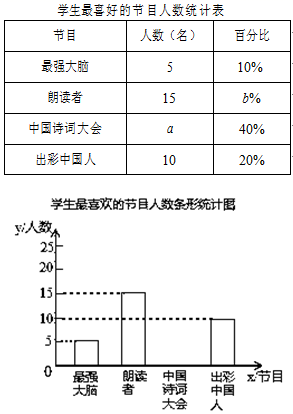
根据以上提供的信息,解答下列问题:
(1)x ,a ,b ;
(2)补全上面的条形统计图;
(3)若该校共有学生5000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
23.(12分)某校计划购进A,B两种树木共100棵进行校园绿化,已知A种树木每棵100元,B种树木每棵80元,因布局需要,购买A种树木的数量不少于B种树木数量的3倍,实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、C
3、D
4、B
5、A
6、D
7、C
8、D
9、D
10、D
11、D
12、A
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、![]()
14、1
15、2
16、两;2;2;22
17、38.8
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)甲、乙两施工队每天分别能完成绿化的面积是100 m2、50 m2;
(2)y=24-2x;
(3)当100≤a≤200时,甲队施工10天,乙队施工4天费用最小,为18800+14a,
当200≤a≤300时,甲队施工11天,乙队施工2天费用最小,为19000+12a
19、(1)见解析;(2)91.5,94,55%;(3)八年级,八年级的中位数和优秀率都高于七年级.
20、证明见解析.
21、 (1) k的值为3,m的值为1;(2)0<n≤1或n≥3.
22、(1)50;20;30;(2)图见解析;(3)2000人。
23、购买A种树木75棵,购买B种树木25棵,实际所花费用最省,最省的费用为8550元.
西藏西藏达孜县2022-2023学年数学七下期末教学质量检测试题含答案: 这是一份西藏西藏达孜县2022-2023学年数学七下期末教学质量检测试题含答案,共6页。试卷主要包含了下列等式正确的是等内容,欢迎下载使用。
西藏拉萨市北京实验中学2022-2023学年七下数学期末监测模拟试题含答案: 这是一份西藏拉萨市北京实验中学2022-2023学年七下数学期末监测模拟试题含答案,共6页。试卷主要包含了计算的值为,方程的解为,下列计算正确的是等内容,欢迎下载使用。
西藏自治区拉萨市达孜区孜县2022-2023学年数学七下期末经典试题含答案: 这是一份西藏自治区拉萨市达孜区孜县2022-2023学年数学七下期末经典试题含答案,共7页。












