


贵州省毕节市七星关区第三实验学校2022-2023学年数学七下期末教学质量检测试题含答案
展开贵州省毕节市七星关区第三实验学校2022-2023学年数学七下期末教学质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题3分,共30分)
1.对于一次函数y=-3x+2,①图象必经过点(-1,-1);②图象经过第一、二、四象限;③当x>1时,y<0;④y的值随着x值的增大而增大,以上结论正确的个数是( )
A.0个 B.1个 C.2个 D.3个
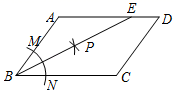
2.已知四边形ABCD的对角线AC、BD相交于点O,给出下列5个条件:①AB∥CD;②OA=OC;③AB=CD;④∠BAD=∠DCB;⑤AD∥BC,从以上5个条件中任选2个条件为一组,能判定四边形ABCD是平行四边形的有( )组.
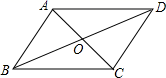
A.4 B.5 C.6 D.7
3.已知多边形的内角和等于外角和,这个多边形的边数为( )
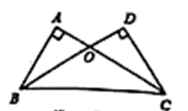
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列命题是真命题的是( )
A.对角线相等的四边形是平行四边形 B.对角线互相平分且相等的四边形是平行四边形
C.对角线互相平分的四边形是平行四边形 D.对角线互相垂直的四边形是平行四边形
5.点A、B、C、D在同一平面内,从AB∥CD,AB=CD,AD∥BC这三条件中任选两个能使四边形ABCD是平行四边形的选法有( )
A.1种 B.2种 C.3种 D.以上都不对
6.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x千米/小时,根据题意,得
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.四边形的内角和为( )
A.180° B.360° C.540° D.720°
8.下列式子中,y不是x的函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.![]() 的取值范围如数轴所示,化简
的取值范围如数轴所示,化简![]() 的结果是( )
的结果是( )
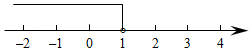
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.如图,添加下列条件仍然不能使▱ABCD成为菱形的是( )
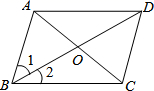
A.AB=BC B.AC⊥BD C.∠ABC=90° D.∠1=∠2
二、填空题(本大题共有6小题,每小题3分,共18分)
11.已知点P(1,2)关于x轴的对称点为P′,且P′在直线y=kx+3上,则k=_______.
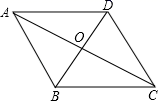
12.如图,在菱形ABCD中,对角线AC,BD交于点O,AB=5,BD=6,则菱形ABCD的面积是_____.
13.如图,在▱ABCD中(AD>AB),用尺规作图作射线BP交AD于点E,若∠D=50°,则∠AEB=___度.
14.如果a2-ka+81是完全平方式,则k=________.
15.已知一组数据为1,10,6,4,7,4,则这组数据的中位数为________________.
16.阅读后填空:
已知:如图,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() .
.
求证:![]() .
.
分析:要证![]() ,可先证
,可先证![]() ;
;
要证![]() ,可先证
,可先证![]() ;
;
而用______可证![]() (填
(填![]() 或
或![]() 或
或![]() ).
).
三、解下列各题(本大题共8小题,共72分)
17.(8分)平行四边形ABCD中,对角线AC上两点E,F,若AE=CF,四边形DEBF是平行四边形吗?说明你的理由.

18.(8分)如图,已知反比例函数 y=![]() 的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为
的图像经过点A(-1,a),过点A作AB⊥x轴,垂足为点B,△AOB的面积为![]() .
.
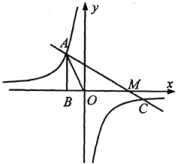
(1)求a、k的值;
(2)若一次函数y=mx+n图像经过点A和反比例函数图像上另一点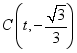 ,且与x轴交于M点,求AM的值:
,且与x轴交于M点,求AM的值:
(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在一次数函数y=bx上,则b= ______.
19.(8分)某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?
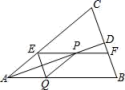
20.(8分)如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任到一点P(点A除外),过点P作EF∥AB,分别交AC、BC于点E、F,作PQ∥AC,交AB于点Q,连接QE与AD相交于点G.
(1)求证:四边形AQPE是菱形.
(2)四边形EQBF是平行四边形吗?若是,请证明;若不是,请说明理由.
(3)直接写出P点在EF的何处位置时,菱形AQPE的面积为四边形EQBF面积的一半.
21.(8分)如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
x+2与x轴、y轴分别交于A、B两点,以A B为边在第二象限内作正方形ABCD.
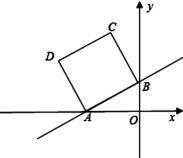
(1)求点A、B的坐标,并求边AB的长;
(2)求点D的坐标;
(3)在x轴上找一点M,使△MDB的周长最小,请求出M点的坐标.
22.(10分)小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
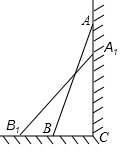
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程______,解方程,得x1=______,x2=______,∴点B将向外移动______米.
(2)解完“思考题”后,小聪提出了如下两个问题:
①(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
②(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?请你解答小聪提出的这两个问题.
23.(10分)如图,矩形纸片![]() 中,已知
中,已知![]() ,折叠纸片使
,折叠纸片使![]() 边落在对角线
边落在对角线![]() 上,点
上,点![]() 落在点
落在点![]() 处,折痕为
处,折痕为![]() ,且
,且![]() ,求线段
,求线段![]() 的长.
的长.
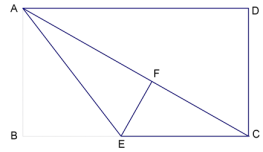
24.(12分)如图,在正方ABCD中,E是AB边上任一点,BG⊥CE,垂足为O,交AC于点F,交AD于点G.
(1)证明:BE=AG;
(2)E位于什么位置时,∠AEF=∠CEB?说明理由.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、B
4、C
5、B
6、A
7、B
8、B
9、D
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、-5
12、24
13、1.
14、±18.
15、5.
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、是,理由见解析.
18、(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
19、(1)每件甲种商品价格为70元,每件乙种商品价格为60元;(2)该商店最多可以购进20件甲种商品
20、(1)见解析;(2)结论:四边形EQBF是平行四边形.见解析;(3)当P为EF中点时,S菱形AEPQ=![]() S四边形EFBQ.
S四边形EFBQ.
21、(1)![]() ;(2)D(-6,4);(3)M(-2,0)
;(2)D(-6,4);(3)M(-2,0)
22、
23、4
24、 (1)见解析;(2)当点E位于线段AB中点时,∠AEF=∠CEB ,理由见解析
2023-2024学年贵州省毕节市七星关区第三实验学校九上数学期末质量检测试题含答案: 这是一份2023-2024学年贵州省毕节市七星关区第三实验学校九上数学期末质量检测试题含答案,共8页。试卷主要包含了下列各式计算正确的是等内容,欢迎下载使用。
2023-2024学年贵州省毕节市七星关区第三实验学校九上数学期末检测试题含答案: 这是一份2023-2024学年贵州省毕节市七星关区第三实验学校九上数学期末检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,在平面直角坐标系中,点E等内容,欢迎下载使用。
贵州省毕节市七星关区第三实验学校2023-2024学年数学八上期末质量跟踪监视模拟试题含答案: 这是一份贵州省毕节市七星关区第三实验学校2023-2024学年数学八上期末质量跟踪监视模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,下列二次根式是最简二次根式的是等内容,欢迎下载使用。












