


福建省厦门第一中学2022-2023学年七年级数学第二学期期末考试模拟试题含答案
展开福建省厦门第一中学2022-2023学年七年级数学第二学期期末考试模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
请考生注意:
1.请用2B铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题(每小题3分,共30分)
1.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF
2.如图,以原点O为圆心,OB长为半径画弧与数轴交于点A,若点A表示的数为x,则x的值为( )
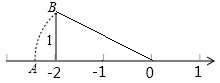
A.![]() B.-
B.-![]() C.
C.![]() -2 D.2-
-2 D.2-![]()
3.如图,将点P(-2,3)向右平移n个单位后落在直线y=2x-1上的点P'处,则n等于( )
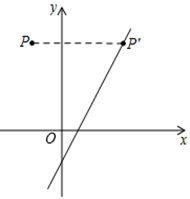
A.4 B.5 C.6 D.7
4.二次根式![]() 在实数范围内有意义,那么
在实数范围内有意义,那么![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
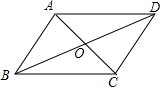
C.![]() D.
D.![]()
5.如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,若添加下列一个条件后,仍然不能证明△ABC≌△DEF,则这个条件是( )
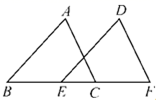
A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF
6.13名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前6名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )
A.方差 B.众数 C.平均数 D.中位数
7.如图,在平行四边形ABCD中,对角线AC、BD交于点O,E是CD的中点,若OE=2,则AD的长为( )
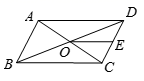
A.2 B.3
C.4 D.5
8.下列各多项式中,不能用平方差公式分解的是( ).
A.a2b2-1 B.4-1.25a2 C.-a2-b2 D.-x2+1
9.用配方法解方程x2+3x+1=0,经过配方,得到( )
A.(x+![]() )2=
)2=![]() B.(x+
B.(x+![]() )2=
)2=![]()
C.(x+3)2=10 D.(x+3)2=8
10.某![]() 边形的每个外角都等于与它相邻内角的
边形的每个外角都等于与它相邻内角的![]() ,则
,则![]() 的值为( )
的值为( )
A.7 B.8 C.10 D.9
二、填空题(本大题共有6小题,每小题3分,共18分)
11.因式分解:x2﹣9y2= .
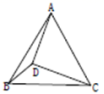
12.如图,点D是等边![]() 内部一点,
内部一点,![]() ,
,![]() ,
,![]() .则
.则![]() 的度数为=________°.
的度数为=________°.
13.在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长备几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为![]() 丈(
丈(![]() 丈
丈![]() 尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面
尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面![]() 尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是
尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是![]() 尺,根据题意,可列方程为__________.
尺,根据题意,可列方程为__________.
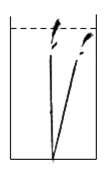
14.如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .
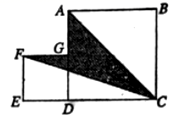
15.如图,正方形ABCD的面积等于25cm2,正方形DEFG的面积等于9cm2,则阴影部分的面积S=______cm2.
16.如果关于![]() 的一次函数
的一次函数![]() 的图像不经过第三象限,那么
的图像不经过第三象限,那么![]() 的取值范围________.
的取值范围________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)已知![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
18.(8分)如图,已知平行四边形ABCD的对角线AC和BD交于点O,且AC+BD=28,BC=12,求△AOD的周长.
19.(8分)某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
20.(8分)现有两家可以选择的快递公司的收费方式如下.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.设物品的重量为x千克,甲、乙公司快递该物品的费用分别为![]() ,
,![]() .
.
(1)分别写出 ![]() 和
和![]() 与x的函数表达式(并写出x的取值范围);
与x的函数表达式(并写出x的取值范围);
(2)图中给出了![]() 与x的函数图象,请在图中画出(1)中
与x的函数图象,请在图中画出(1)中![]() 与x的函数图象(要求列表,描点).
与x的函数图象(要求列表,描点).
x | … | _____ | _____ | … |
y | … | _____ | _____ | … |
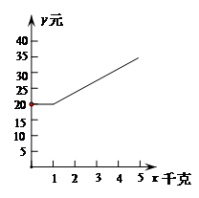
21.(8分)如图,在四边形ABCD中,∠ABC=90°,E、F分别是AC、CD的中点,AC=8,AD=6,∠BEF=90°,求BF的长.

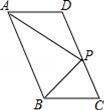
22.(10分)如图,![]() 、
、![]() 相交于点
相交于点![]() ,且
,且![]() 是
是![]() 、
、![]() 的中点,点
的中点,点![]() 在四边形
在四边形![]() 外,且
外,且![]() ,
,
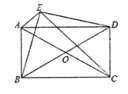
求证:边形![]() 是矩形.
是矩形.
23.(10分)武汉某中学为了了解全校学生的课外阅读的情况,随机抽取了部分学生进行阅读时间调查,现将学生每学期的阅读时间![]() 分成
分成![]() 、
、![]() 、
、![]() 、
、![]() 四个等级(
四个等级(![]() 等:
等:![]() ,
,![]() 等:
等:![]() ,
,![]() 等:
等:![]() ,
,![]() 等:
等:![]() ;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
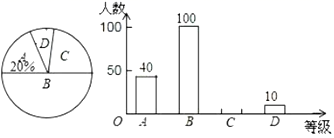
(1)![]() 组的人数是____人,并补全条形统计图.
组的人数是____人,并补全条形统计图.
(2)本次调查的众数是_____等,中位数落在_____等.
(3)国家规定:“中小学每学期的课外阅读时间不低于60小时”,如果该校今年有3500名学生,达到国家规定的阅读时间的人数约有_____人.
24.(12分)为积极响应新旧功能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为35万元时,年销售量为550台;每台售价为40万元时,年销售量为500台.假定该设备的年销售量![]() (单位:台)和销售单价
(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于60万元,如果该公司想获得8000万元的年利润,则该设备的销售单价应是多少万元?
参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、A
4、A
5、D
6、D
7、C
8、C
9、B
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() .
.
12、1
13、![]()
14、24.
15、![]()
16、![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)![]() ;(2)13
;(2)13
18、1
19、(I)200,100+5x,180,9x;(II)选择方式一付费方式,他游泳的次数比较多(III)当20<x<25时,小明选择方式二的付费方式,当x=25时,小明选择两种付费方式一样,当x>25时,小明选择方式一的付费方式
20、(1)![]() ,
,![]() ;
;
(2)
x | … | __1___ | __2___ | _3___ | … |
y | … | ___17__ | __24___ | _31___ | … |
图象见解析
21、2
22、见解析.
23、(1)50;(2)众数是B等,中位数落在C等;(3)3325人.
24、(1)年销售量![]() 与销售单价
与销售单价![]() 的函数关系式为
的函数关系式为![]() ;(2)该设备的销售单价应是50万元/台.
;(2)该设备的销售单价应是50万元/台.
福建省厦门五中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案: 这是一份福建省厦门五中学2022-2023学年七年级数学第二学期期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
福建省厦门市五中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案: 这是一份福建省厦门市五中学2022-2023学年七年级数学第二学期期末达标检测模拟试题含答案,共7页。试卷主要包含了点P到x轴的距离是,若式子有意义,则的取值范围为等内容,欢迎下载使用。
2022-2023学年福建省厦门市逸夫中学七年级数学第二学期期末学业水平测试模拟试题含答案: 这是一份2022-2023学年福建省厦门市逸夫中学七年级数学第二学期期末学业水平测试模拟试题含答案,共8页。试卷主要包含了已知点A, 下列命题等内容,欢迎下载使用。












