


浙江省金华兰溪市实验中学2022-2023学年数学七下期末达标检测试题含答案
展开浙江省金华兰溪市实验中学2022-2023学年数学七下期末达标检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题(每小题3分,共30分)
1.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是( )
A. B.
B.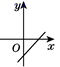 C.
C.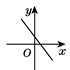 D.
D.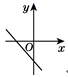
2.下列说法正确的是( )
A.为了解昆明市中学生的睡眠情况,应该采用普查的方式
B.数据2,1,0,3,4的平均数是3
C.一组数据1,5,3,2,3,4,8的众数是3
D.在连续5次数学周考测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定
3.如图,矩形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() ,
,![]() ,则
,则![]() 的长度为( )
的长度为( )

A.1 B.2 C.![]() D.
D.![]()
4.如图,四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是( )
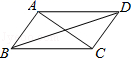
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
5.若关于x的不等式组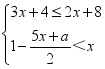 有且仅有5个整数解,且关于y的分式方程
有且仅有5个整数解,且关于y的分式方程![]() 有非负整数解,则满足条件的所有整数a的和为( )
有非负整数解,则满足条件的所有整数a的和为( )
A.12 B.14 C.21 D.33
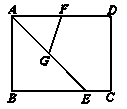
6.已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
7.正比例函数y=mx的图象经过点A(m,4),且y的值随x值的增大而减小,则m=( )
A.2 B.-2 C.4 D.-4
8.下列计算:![]() ,其中结果正确的个数为( )
,其中结果正确的个数为( )
A.1 B.2 C.3 D.4
9.下列命题中,是真命题的是( )
A.平行四边形的对角线一定相等
B.等腰三角形任意一条边上的高线、中线和角平分线都三线合一
C.三角形的中位线平行于第三边并且等于它的一半
D.三角形的两边之和小于第三边
10.对于反比例函数![]() ,当
,当![]() 时,y的取值范围是( )
时,y的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本大题共有6小题,每小题3分,共18分)
11.计算![]() -
-![]() =_______.
=_______.
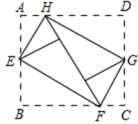
12.如图,将矩形ABCD的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=8cm,EF=15cm,则边AD的长是______cm.
13.已知:线段![]()
求作:菱形![]() ,使得
,使得![]() 且
且![]() .
.
以下是小丁同学的作法:
①作线段![]() ;
;
②分别以点![]() ,
,![]() 为圆心,线段
为圆心,线段![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ;
;
③再分别以点![]() ,
,![]() 为圆心,线段
为圆心,线段![]() 的长为半径作弧,两弧交于点
的长为半径作弧,两弧交于点![]() ;
;
④连接![]() ,
,![]() ,
,![]() .
.
则四边形![]() 即为所求作的菱形.(如图)
即为所求作的菱形.(如图)
老师说小丁同学的作图正确.则小丁同学的作图依据是:_______.
14.如图,点![]() 在双曲线
在双曲线![]() 上,
上,![]() 为
为![]() 轴上的一点,过点
轴上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() 的面积是3,则
的面积是3,则![]() __.
__.

15.一根木杆在离地![]() 米处折断,木杆的顶端在离木杆底端
米处折断,木杆的顶端在离木杆底端![]() 米处,则木杆折断之前的高度为__________米.
米处,则木杆折断之前的高度为__________米.
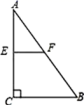
16.如图,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E、F分别为AC和AB的中点,则EF=____________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)按要求解不等式(组)
(1)求不等式![]() 的非负整数解.
的非负整数解.
(2)解不等式组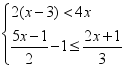 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
18.(8分)已知,如图,O为正方形对角线的交点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
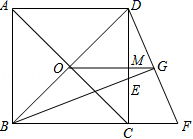
(1)求证:△BCE≌△DCF.
(2)判断OG与BF有什么关系,证明你的结论.
(3)若DF2=8-4![]() ,求正方形ABCD的面积?
,求正方形ABCD的面积?
19.(8分)在昆明市“创文”工作的带动下,某班学生开展了“文明在行动”的志愿者活动,准备购买一些书包送到希望学校,已知A品牌的书包每个40元,B品牌的书包每个42元,经协商:购买A品牌书包按原价的九折销售;购买B品牌的书包10个以内(包括10个)按原价销售,10个以上超出的部分按原价的八折销售.
(1)设购买x个A品牌书包需要y1元,求出y1关于x的函数关系式;
(2)购买x个B品牌书包需要y2元,求出y2关于x的函数关系式;
(3)若购买书包的数量超过10个,问购买哪种品牌的书包更合算?说明理由.
20.(8分)解不等式组,并将解集在数轴上表示出来.
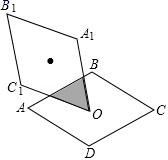
21.(8分)如图,在平面内,菱形 ABCD 的对角线相交于点 O,点 O 又是菱形B1A1OC1的一个顶点,菱形 ABCD≌菱形 B1A1OC1,AB=BD=1.菱形B1A1OC1 绕点 O 转动,求两个菱形重叠部分面积的取值范围,请说明理由.
22.(10分)如图,反比例函数y1=![]() 与一次函数y2=mx+n相交于A(﹣1,2),B(4,a)两点,AE⊥y轴于点E,则:
与一次函数y2=mx+n相交于A(﹣1,2),B(4,a)两点,AE⊥y轴于点E,则:
(1)求反比例函数与一次函数的解析式;
(2)若y1≤y2则直接写出x的取值范围;
(3)若M为反比例函数上第四象限内的一个动点,若满足S△ABM=S△AOB,则求点M的坐标.

23.(10分)先化简,再求值:![]() ÷(x﹣
÷(x﹣![]() ),其中x=
),其中x=![]() +1.
+1.
24.(12分)我市飞龙商贸城有甲、乙两家商店均出售白板和白板笔,并且标价相同,每块白板50元,每支白板笔4元.某校计划购买白板30块,白板笔若干支(白板笔数不少于90支),恰好甲、乙两商店开展优惠活动,甲商店的优惠方式是白板打9折,白板笔打7折;乙商店的优惠方式是白板及白板笔都不打折,但每买2块白板送白板笔5支.
(1)以x(单位:支)表示该班购买的白板笔数量,y(单位:元)表示该班购买白板及白板笔所需金额.分别就这两家商店优惠方式写出y关于x的函数解析式;
(2)请根据白板笔数量变化为该校设计一种比较省钱的购买方案.
参考答案
一、选择题(每小题3分,共30分)
1、B
2、C
3、B
4、C
5、B
6、D
7、B
8、D
9、C
10、A
二、填空题(本大题共有6小题,每小题3分,共18分)
11、2![]()
12、![]()
13、三边都相等的三角形是等边三角形;等边三角形的每个内角都是60°;四边都相等的四边形是菱形
14、-6
15、![]()
16、3;
三、解下列各题(本大题共8小题,共72分)
17、(1)非负整数解为1、2、3、4;(2)-3<x≤1,数轴上表示见解析
18、(2)证明见解析.(2)OG∥BF且OG=![]() BF;证明见解析.(3)2.
BF;证明见解析.(3)2.
19、(1)y1=36x;(2)当0≤x≤10时,y2=42x,当x>10时,y2=33.6x+84;(3)若购买35个书包,选A,B品牌都一样,若购买35个以上书包,选B品牌划算,若购买书包个数超过10个但小于35个,选A品牌划算
20、不等式组的解集是﹣1<x≤3.
21、![]() ≤s
≤s ![]() .
.
22、(1)![]() ,
,![]() ;(2)x≤﹣1或0<x≤1;(3)点M的坐标(2,﹣1)或(3+
;(2)x≤﹣1或0<x≤1;(3)点M的坐标(2,﹣1)或(3+![]() ,
,![]() ).
).
23、![]() .
.
24、(1)到甲商店购买所需金额为: y=2.8x+1350;到乙商店购买所需金额为:y=4x+1200;(2)购买白板笔在多于1支时到甲商店,少于1支时到乙商店,恰好购买1支时到甲商店和到乙商店一样
2023-2024学年浙江省金华兰溪市实验中学数学九上期末监测模拟试题含答案: 这是一份2023-2024学年浙江省金华兰溪市实验中学数学九上期末监测模拟试题含答案,共7页。试卷主要包含了边长为2的正六边形的面积为等内容,欢迎下载使用。
2023-2024学年浙江省金华兰溪市实验中学八年级数学第一学期期末达标测试试题含答案: 这是一份2023-2024学年浙江省金华兰溪市实验中学八年级数学第一学期期末达标测试试题含答案,共7页。试卷主要包含了用科学记数法表示,已知等内容,欢迎下载使用。
2023-2024学年浙江省金华市兰溪市实验中学八年级数学第一学期期末达标检测试题含答案: 这是一份2023-2024学年浙江省金华市兰溪市实验中学八年级数学第一学期期末达标检测试题含答案,共6页。试卷主要包含了考生要认真填写考场号和座位序号,①实数和数轴上的点一一对应,下列代数式中,是分式的为,下列计算正确的是,下列因式分解结果正确的有,计算等内容,欢迎下载使用。












