


江西省吉安市永新县2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案
展开江西省吉安市永新县2022-2023学年七年级数学第二学期期末教学质量检测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.解分式方程![]() 时,在方程的两边同时乘以(x﹣1)(x+1),把原方程化为x+1+2x(x﹣1)=2(x﹣1)(x+1),这一变形过程体现的数学思想主要是( )
时,在方程的两边同时乘以(x﹣1)(x+1),把原方程化为x+1+2x(x﹣1)=2(x﹣1)(x+1),这一变形过程体现的数学思想主要是( )
A.类比思想 B.转化思想 C.方程思想 D.函数思想
2.将一次函数![]() 图像向下平移
图像向下平移![]() 个单位,与双曲线
个单位,与双曲线![]() 交于点A,与
交于点A,与![]() 轴交于点B,则
轴交于点B,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
4.若分式![]() 有意义,则实数x的取值范围是( )
有意义,则实数x的取值范围是( )
A.x>5 B.x<5 C.x=5 D.x≠5
5.不等式组![]() 的解集在数轴上表示正确的是
的解集在数轴上表示正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图所示,将一张正方形纸片对折两次,然后在上面打3个洞,则纸片展开后是
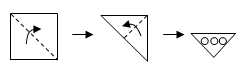
A.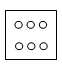 B.
B.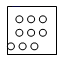 C.
C.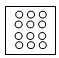 D.
D.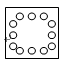
7.分式方程![]() 的解为( )
的解为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.点A,B,C,D都在如图所示的由正方形组成的网格图中,且线段CD与线段AB成位似图形,则位似中心为( )
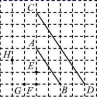
A.点E B.点F
C.点H D.点G
9.如图,P是矩形ABCD的AD边上一个动点,矩形的两条边AB、BC长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )
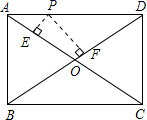
A.4.8 B.5 C.6 D.7.2
10.某中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小明的三项成绩(百分制)依次是90,80,94,小明这学期的体育成绩是( )
A.88 B.89 C.90 D.91
二、填空题(本大题共有6小题,每小题3分,共18分)
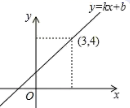
11.一次函数![]() (k,b为常数,
(k,b为常数,![]() )的图象如图所示,根据图象信息可得到关于x的方程
)的图象如图所示,根据图象信息可得到关于x的方程![]() 的解为__________.
的解为__________.
12.菱形的两条对角线长分别为![]() cm和
cm和![]() cm,则该菱形的面积__________
cm,则该菱形的面积__________![]() .
.
13.当m_____时,函数y=(m﹣3)x﹣2中y随x的增大而减小.
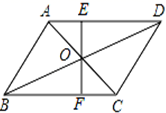
14.已知:在▱ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则▱ABCD的面积是_____.
15.古语说:“春眠不觉晓”,每到初春时分,想必有不少人变得嗜睡,而且睡醒后精神不佳.我们可以在饮食方面进行防治,比如以下食物可防治春困:香椿、大蒜、韭菜、山药、麦片.春天即将来临时,某商人抓住商机,购进甲、乙、丙三种麦片,已知销售每袋甲种麦片的利润率为10%,每袋乙种麦片的利润率为20%,每袋丙种麦片的利润率为30%,当售出的甲、乙、丙三种麦片的袋数之比为1:3:1时,商人得到的总利润率为22%;当售出的甲、乙、丙三种变片的袋数之比为3:2:1时,商人得到的总利润率为20%:那么当售出的甲、乙、丙三种麦片的袋数之比为2:3;4时,这个商人得到的总利润率为_____(用百分号表最终结果).
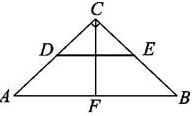
16.如图,在Rt△ABC中,∠ACB=90°,点D、E、F分别是三边的中点,CF=8cm,则线段DE=________cm.
三、解下列各题(本大题共8小题,共72分)
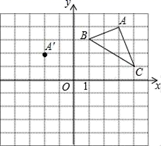
17.(8分)在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点A′的坐标是(﹣2,2),现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′(不写画法);
(2)并直接写出点B′、C′的坐标:B′( )、C′( );
(3)若△ABC内部一点P的坐标为(a,b),则点P的对应点P′的坐标是( ).
18.(8分)孝感市委市政府为了贯彻落实国家的“精准扶贫”战略部署,组织相关企业开展扶贫工作,博大公司为此制定了关于帮扶A、B两贫困村的计划.今年3月份决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗.已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
目的地 费用 车型 | A村(元/辆) | B村(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总运费为y元;
①试求出y与x的函数解析式;
②若运往A村的鱼苗不少于108箱,请你写出使总运费最少的货车调配方案,并求出最少运费.
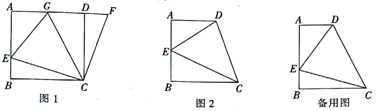
19.(8分)如图1,在正方形ABCD中,点E是AB上一点,点F是AD延长线上一点,且DF=BE,连接CE、CF.
(1)求证:CE=CF.
(2)在图1中,若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗;为什么;
(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题,如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,且∠DCE=45°.
①若AE=6,DE=10,求AB的长;
②若AB=BC=9,BE=3,求DE的长.
20.(8分)如图,在平面直角坐标系![]() 中,位于第二象限的点
中,位于第二象限的点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,直线
对称,直线![]() 经过点
经过点![]() ,且与反比例函数
,且与反比例函数![]() 的图像交于点
的图像交于点![]() .
.
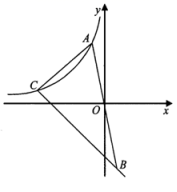
(1)当点![]() 的横坐标是-2,点
的横坐标是-2,点![]() 坐标是
坐标是![]() 时,分别求出
时,分别求出![]() 的函数表达式;
的函数表达式;
(2)若点![]() 的横坐标是点
的横坐标是点![]() 的横坐标的4倍,且
的横坐标的4倍,且![]() 的面积是16,求
的面积是16,求![]() 的值.
的值.
21.(8分)在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
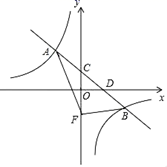
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式![]() 的解集.
的解集.
22.(10分)如图,已知四边形![]() 为正方形,
为正方形,![]() ,点
,点![]() 为对角线
为对角线![]() 上一动点,连接
上一动点,连接![]() ,过点
,过点![]() 作
作![]() .交
.交![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
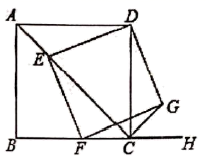
(1)求证:矩形![]() 是正方形;
是正方形;
(2)探究:![]() 的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
23.(10分)如图,四边形ABCD是菱形,AC=24, BD=10,DH⊥AB 于点H,求菱形的面积及线段DH的长.

24.(12分)如图,已知直线y1经过点A(-1,0)与点B(2.3),另一条直线y2经过点B,且与x轴交于点P(m.0).
(1)求直线y1的解析式;
(2)若三角形ABP的面积为![]() ,求m的值.
,求m的值.

参考答案
一、选择题(每小题3分,共30分)
1、B
2、B
3、B
4、D
5、C
6、D
7、C
8、B
9、A
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、x=1
12、![]()
13、m<3
14、1
15、25%.
16、8
三、解下列各题(本大题共8小题,共72分)
17、(1)答案见解析;(2)B′(﹣4,1)、C′(﹣1,﹣1);(3)(a﹣5,b﹣2).
18、(1)这15辆车中大货车用8辆,小货车用7辆;(2)①y=100x+9400(3≤x≤8,且x为整数);②使总运费最少的调配方案是:7辆大货车、3辆小货车前往A村;1辆大货车、4辆小货车前往B村.最少运费为10100元.
19、(1)证明见解析;(2)成立;(3)①12;②7.1
20、(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
21、(1)y=﹣![]() x+
x+![]() ,y=
,y=![]() ;(2)12;(3) x<﹣2或0<x<4.
;(2)12;(3) x<﹣2或0<x<4.
22、(1)见解析 (2)是定值,8
23、![]()
24、 (1) y1=x+1;(2)m=1或m=-2.
江西省永新县2023-2024学年数学九上期末达标检测模拟试题含答案: 这是一份江西省永新县2023-2024学年数学九上期末达标检测模拟试题含答案,共8页。试卷主要包含了在做针尖落地的实验中,正确的是,如图,太阳在A时测得某树,抛物线的顶点坐标是,若α为锐角,且,则α等于等内容,欢迎下载使用。
2023-2024学年江西省吉安永新县联考九年级数学第一学期期末教学质量检测试题含答案: 这是一份2023-2024学年江西省吉安永新县联考九年级数学第一学期期末教学质量检测试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,反比例函数,下列说法不正确的是等内容,欢迎下载使用。
2023-2024学年江西省吉安市永新县八上数学期末联考试题含答案: 这是一份2023-2024学年江西省吉安市永新县八上数学期末联考试题含答案,共7页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。












