3升4奥数拓展：复杂搭配问题-数学四年级上册人教版

这是一份3升4奥数拓展：复杂搭配问题-数学四年级上册人教版，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
3升4奥数拓展：复杂搭配问题-数学四年级上册人教版 一、选择题1．A、B、C、D、E五名同学进行象棋比赛，每两个都要比赛1场，到现在为止，A已赛了2场，B已赛了4场，C已赛了3场，D已赛1场，那么E赛了（    ）场。A．2 B．3 C．4 D．52．用1元2元5元的人民币各一张，选其中一张或几张，不能得到的面值是（    ）。A．4元 B．5元 C．6元 D．7元3．学校组织春游活动因故提前了，张老师要尽快通知到每一位学生，如果用打电话的方式，每分钟通知1人，每人接到电话后立即通知其他不知道这一信息的同学，全班40位同学，最快（    ）分钟才能通知到全班同学。A．4 B．5 C．6 D．74．参观比赛的两队选手，在比赛结束后互相握手，所有的人握了10次手，有（    ）人互相握手。A．4 B．10 C．5 D．95．将7个点连成线段，任意三点不在同一条直线上，最多可以连成（    ）。A．7条 B．12条 C．21条 D．28条6．按照中国篮球职业联赛组委会的规定，各队队员的号码可以选择的范围是0～55号，但选择两位数的号码时，每位数字均不能超过5，那么，可供每支球队选择的号码共（ ）个。A．34 B．35 C．40 D．56 二、填空题7．2022年卡塔尔世界杯，一共32支球队参加比赛，分成8个小组，每小组4支球队进行第一轮的单循环赛，请问每个小组要比赛(        )场。8．玲玲、丽丽、明明、陈红和嘉豪5名同学互相握手，每两人握一次，一共握手(        )次。9．开学时4位好朋友每2人拥抱一次，共要拥抱(        )次；他们还要站成一排合影，小明站在最左边，其他人的位置可自由安排，共有(        )种站法。10．A、B、C、D、E五人进行乒乓球比赛，每两个人都要赛一场。现在A、D赛了4场，B、C各自赛了3场，E至少赛(        )场。11．李老师要把语文、数学、英语、科学4本书（各1本）分给丽丽、阳阳、聪聪三个同学，每个同学至少分其中的一本，一共有(      )种不同的分法。12．有2名男生和2名女生如图站成一排拍照，那么他们一共有(        )种不同的站法。13．5名象棋爱好者进行比赛，规定每两人比赛一局，经过一段时间后统计，甲已赛了4局，乙已赛了3局，丙已赛了2局，丁已赛了1局，则此时戊已赛了(        )局。14．一种巧克力有4块装和6块装两种包装方式，要购买这种巧克力26块，有(        )种不同的买法，在解决这一问题时用(        )的思想方法可以不重复不遗漏的找到所有买法。 三、解答题15．有A、B、C三片荷叶，青蛙“呱呱”在荷叶A上，每次它都会从一片荷叶跳到另一片荷叶上，结果它跳了3次之后，不在荷叶A上，那么它一共有多少种不同的跳法？   16．小、莫、萱三人玩传球游戏，每次持球的人都可以把球传给另外两个人中的任何一个，先由小拿球，经过4次传球之后，球又回到了小的手里，那么一共有多少种不同的传球过程？   17．如下图，如果小高站在1号地毯上，他想要走到5号地毯上，每次只能走到相邻的编号（两个六边形如果有公共边就成为相邻），而且只能向右边走（例如1→2→3→5就是一种可能的走法） ，那么小高一共有多少种不同的走法？   18．王老师有一个带密码锁的公文包，但是他忘记了密码，只记得密码是一个三位数，这个三位数的个位数字比十位数字大，十位数字比百位数字大，并且没有比5大的数字，那么王老师最多试几次就肯定能打开这个公文包？   19．17支排球队分成三组，其中两组各6支队，第三组5支队，第一阶段各组进行单循环比赛；第二阶段，由各组前两名举行单循环比赛，决出冠亚军，共需举行多少场比赛？若第二阶段中，原同一组的两队免赛，共需举行多少场比赛？若17支球队不分组，直接利用单循环赛制，共要赛多少场？   20．某沿海城市管辖7个县，这7个县的位置如图。现用红、黑、绿、蓝、紫五种颜色给下图染色，要求任意相邻的两个县染不同颜色，共有多少种不同的染色方法？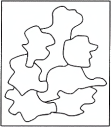
参考答案：1．A【分析】分析题意，B赛了4场，则B是和A、C、D、E每人赛了1场，而D只赛了1场，则一定是和B赛的，C赛了3场，是和A、B、E赛的，而A赛了2场，是和B、C赛的，那么E一定和B、C赛了。【详解】由分析可知：E赛了2场。故答案为：A【点睛】本题考查的是学生的逻辑推理能力，根据每个人最多只能比赛4场作为突破口，对A、B、C、D逐个进行推理，即可找出E进行比赛的场次。2．A【分析】根据题意，分三种情况：（1）选出其中的一张；（2）选出其中的两张；（3）选出其中的三张；分别求出每种情况下可以组成多少种不同面值的人民币，分别是哪些面值的，进而判断选择即可。【详解】根据分析可得：（1）选出其中的一张时，可以组成1元、2元和5元面值的人民币；（2）选出其中的两张时，1＋2＝3（元）1＋5＝6（元）2＋5＝7（元），可以组成3元、6元和7元面值的人民币；（3）选出其中的三张时，1＋2＋5＝8（元）可以组成8元面值的人民币。所以，组成1元、2元、5元、3元、6元、7元和8元面值的人民币；但不能组成面值4元的人民币。故答案为：A【点睛】此题主要考查了搭配问题，考查了分类讨论思想的应用，要熟练掌握，注意不能多数、漏数。3．C【分析】老师先用一分钟通知1个学生，第二分钟由老师和学生分别通知一个学生，现在通知的是1＋2＝3＝2×2－1，第三分钟通知的是3＋4＝2×2×2－1。据此类推解答。【详解】第一分钟通知到1个学生；第二分钟最多可通知到2×2－1＝3个学生；第三分钟最多可通知到2×2×2－1＝7个学生；第四分钟最多可通知到2×2×2×2－1＝15个学生；第五分钟最多可通知到2×2×2×2×2－1＝31个学生；第六分钟可通知到63个学生；最少要用6分钟可以通知40人；故答案为：C。【点睛】此题考查的是应用规律解决实际问题的能力。4．C【分析】每个人都要和他自己以外的人握手一次，但是两个人之间只握手一次，所有的人握了10次手×2＝人数×人数－1，把选项的人数一一代入等量关系，判断答案。【详解】根据分析可得，总握手次数＝人数×人数－1，10次是去掉重复后的次数，总握手次数＝10×2＝20（次）A．4×（4－1）＝4×3＝12（次）B．10×（10－1）＝10×9＝90（次）C．5×（5－1）＝5×4＝20（次）D．9×（9－1）＝9×8＝72（次）故答案选：C。【点睛】本题考查搭配问题，找出等量关系是解题的关键。5．C【分析】每一条线段有两个端点，从7个点中选一个点作为端点有7种方法，而选第二个点有6种方法，共有7×6种方法。但是因一条线段重复一次，故实际上是7×6÷2条线段。【详解】7×（7－1）÷2＝7×3＝21（条）所以7个点最多可以连成21条线段。故选：C。【点睛】本题考查了排列组合知识的灵活应用，解答此题的关键是理解两点只能连一条线段，所以要排除重合的情况。6．C【分析】根据题意，可供选择的号码可以分为一位数和两位数两大类，一位数总共有10个，两位数要求每位数字均不能超过5，那么可以选择0、1、2、3、4、5，考虑到首位不为0，那么十位数字5种选法，个位数字6种选法。 【详解】其中一位数可以为0~9，有10种选择；两位数的十位可以为1~5，个位可以为0~5，根据乘法原理，两位数号码有5×6＝30种选择；所以可供选择的号码共有10＋30＝40种。故答案选：C。【点睛】应用加乘原理求解计数问题时，应该遵循加法分类、乘法分步的原则。7．6【分析】每小组4支球队，每2个球队踢一场，求一共要踢多少场，就是求一共有几种不同的组合方法。如下图，把4个球队一字排开，先把每个球队与其他球队分别连上线，再数一数一共连了几条线，连了几条线，就要踢几场。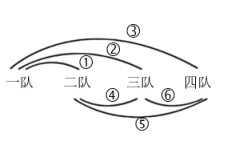【详解】如上图：3＋2＋1＝6（场）所以每个小组要比赛6场。【点睛】稍复杂的组合问题可以用图示连线的方法来解决，组合过程中不考虑事物的先后顺序，只需注意不同组合中的元素。8．10【分析】由于每个人都要和另外的4人握手，一共要握5×4＝20（次）；又因为两个人只握一次，去掉重复计算的情况，实际只握20÷2＝10（次）据此解答。【详解】（5－1）×5÷2＝4×5÷2＝10（次）每两人握一次，一共握手10次。【点睛】本题考查了两两搭配问题的实际应用，要注意去掉重复计算的情况，如果人比较少可以用枚举法解答，如果人数比较多可以用公式：握手次数＝人数×（人数－1） ÷2解答。9．     6     6【分析】4位好朋友每2人拥抱一次，也就是每个人都要和另外3人拥抱一次，一共要拥抱3×4＝12（次）；又因为两个人只拥抱一次，去掉重复计算的情况，实际只拥抱12÷2＝6（次）；小明的位置是确定的，把小明除外，3个人站在最右边的可能是3人中的任意一人，有3种不同的方法；第二位上还剩2人选择，有2种不同的站法；第三位还有1人，有1种方法，它们的积就是全部的站法。【详解】拥抱次数：（4－1）×4÷2＝3×4÷2＝6（次）站法：3×2×1＝6（种）【点睛】本题考查了搭配问题的实际应用，两两搭配时要注意去掉重复计算的情况，如果人比较少可以用枚举法解答，如果人数比较多可以用公式：实际次数＝人数×（人数－1） ÷2；简单的排列问题可以采用依次列举或连线的方法找出所有不同的排列方法，可以先确定第一个位置，再确定第二、第三个位置。10．2【分析】五人进行乒乓球比赛，每两个人都要赛一场，即每人都要和另外四个人赛一场，共赛4场。现在A、D都赛了4场，即A和D和除了自己以外的其它四人都赛了一场，B、C都赛了3场，则B这三场可和A、C、D各赛一场，C可和A、B、D各赛一场，所以E至少赛了2场，即和A、D各赛一场。【详解】根据分析得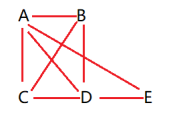，E至少赛2场。【点睛】根据每人需要比赛的总场数及A、B、C、D已赛的场数进行推理分析，从而得出结论是完成本题的关键。11．36【分析】把语文、数学、英语、科学4本书分给丽丽、阳阳、聪聪三个同学，这里既要考虑书的不同，也要考虑人的区别，而每个同学至少分其中的一本，那么只能是把4本书按照1、1、2进行分配，然后考虑人数的不同进行枚举。【详解】先考虑把4本书按照1、1、2进行分配，有6种情况；语文和数学、英语、科学；语文和英语、数学、科学；语文和科学、数学、英语；数学和英语、语文、科学；数学和科学、语文、英语；英语和科学、语文、数学；比如第一种情况，按照语文和数学、英语、科学分组，然后考虑人数的不同，又有6种不同的情况；（从左往右依次是丽丽、阳阳、聪聪得到的书）①语文和数学，英语，科学；②语文和数学，科学，英语；③英语，语文和数学，科学；④英语，科学，语文和数学；⑤科学，语文和数学，英语；⑥科学，英语，语文和数学；其余每种情况都是类似的，，总共有36种不同的分法。【点睛】本题考查的是计数问题，枚举法是求解此类问题最基础的方法，这里需要考虑顺序的影响。12．24【分析】4人排成一排，第1个位置可以由4种选择，第2个位置有3种选择，第3个位置有2种选择，最后1个位置只有1种选择，相乘即可。【详解】4×3×2＝12×2＝24（种）【点睛】分步计数原理用乘法计算。13．2【分析】5个人两两之间比赛，那么每个人要和另外4人比赛，每人赛4场，再根据ABCD四人赛的场次进行推算。【详解】每人最多赛4场；甲已经赛了4局，说明它和另外的四人都赛了一局，包括丙和戊；丁赛了1局，说明他只和A进行了比赛，没有和其它选手比赛；乙赛了3局，他没有和丁比赛，是和另外的三人进行了比赛，包括丙和戊；丙赛了2局，是和A、B进行的比赛，没有和戊比赛所以戊只和A、B进行了比赛，一共是2局；【点睛】本题根据每个人最多只能比赛4场作为突破口，进行逐个推理，找出戊进行比赛的场次。14．     两     列举【分析】根据购买巧克力总块数，分情况讨论购买1包、2包、3包……4块装的巧克力时，6块装需要的数量是否为整数，两种包装购买的数量均为整数时符合条件。【详解】购买2包4块装的巧克力和3包6块装的巧克力：2×4＋3×6＝26（块）；购买5包4块装的巧克力和1包6块装的巧克力：5×4＋1×6＝26（块）；所以要购买这种巧克力26块，有（   两   ）种不同的买法，在解决这一问题时用列举的思想方法可以不重复不遗漏的找到所有买法。【点睛】用列举法逐一筛选可以不重复不遗漏的找到所有买法。15．6种【分析】根据题意，第一次跳之后可能在B荷叶或者C荷叶上，最后跳了3次之后，排除掉在A荷叶上的，即可得解。【详解】第一次可跳在B、C荷叶上，据此画出树形图如下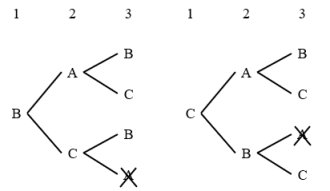：由图可知，共6种。答：它一共有6种不同的跳法。【点睛】树形图是枚举法的一种，可以使我们的枚举过程更加直观，有条理又不易重复或遗漏。16．6种【分析】先考虑第1次有多少种传法？然后用树形图画出每次传球后给谁。要注意只有第4次传球后回到小手上的才是符合题意的传法。【详解】由题意可知，小先拿球，则第1次可以给莫也可以给萱。由题意画树形图如下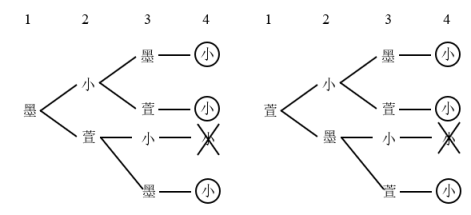：由图可知，共有6种情况符合要求。答：一共有6种不同的传球过程。【点睛】根据题意分析出第1次只能给莫或萱，据此正确画出树形图是解题关键。17．5种【分析】根据题意，小高第一步可以走到2号地毯或3号地毯，据此注意分析即可，注意题目中的限定条件：相邻编号地毯和只能向右走，另外只有结束在5号地毯的才符合题意。【详解】根据题意，画图如下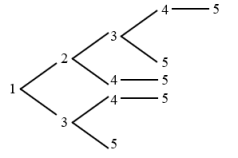：数一数可知，一共5种可能。答：小高一共有5种不同的走法。【点睛】解答此类问题，按照树形图的画法逐一画出所有的分叉即可。注意不重复不遗漏。18．10次【分析】由“这个三位数的个位数字比十位数字大，十位数字比百位数字大”可知，百位数字最小，先考虑百位数字最小有几种情况。分别把这些情况作为“树根”，画出树形图解答即可。【详解】由题意可知，百位数字最小，分别用1、2、3三个数作为树根，可以画出三幅树形图，如下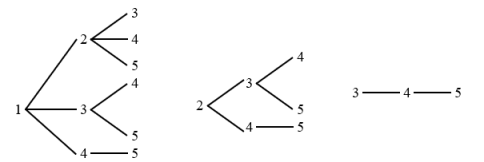：即：百位是1时有6种情况，百位是2时有3种情况，百位是3时有1种情况。答：王老师最多试10次就肯定能打开这个公文包。【点睛】画树状图的关键一是确定层数，二是确定每层分叉的个数。一般先从“树根”开始，然后长枝、分叉，最终只需要数一下结果数目即可得解。19．55场；52场；136场【分析】单循环赛制的场数＝队伍数×（队伍数－1）÷2，根据这个公式分别计算；注意第二种情况下，三组各有两队不需要再比赛，因此要减少3场比赛。【详解】6×（6－1）÷2×2＋5×（5－1）÷2＝6×5÷2×2＋5×4÷2＝30＋10＝40（场）40＋6×（6－1）÷2＝40＋6×5÷2＝40＋15＝55（场）55－3＝52（场）17×（17－1）÷2＝17×16÷2＝136（场）答：第一种情况共需要55场；第二种情况共需要52场；第三种情况共需要136场。【点睛】本题考查排列组合的知识，关键是掌握循环赛问题的求解方法。20．4860种【分析】如图，为了便于观察，在保持相邻关系不变的情况下可以把左图改画成右图，然后按照A、B、C、D、E、F、G的染色顺序进行染色。【详解】如图所示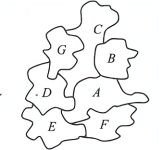：第1步：先染区域，有5种颜色可供选择；第2步：再染区域，由于不能与同色，所以区域的染色方式有4种；第3步：染区域，由于不能与、同色，所以区域的染色方式有3种；第4步：染区域，由于不能与、同色，所以区域的染色方式有3种；第5步：染区域，由于不能与、同色，所以区域的染色方式有3种；第6步：染区域，由于不能与、同色，所以区域的染色方式有3种；第7步：染区域，由于不能与、同色，所以区域的染色方式有3种。根据分步计数的乘法原理，共有种不同的染色方法。答：共有4860种不同的染色方法。【点睛】本题考查的是计数中的染色问题，染色的时候一般从接触面最多的一块开始。