云南省重点中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题含答案

云南省重点中学2022-2023学年七年级数学第二学期期末学业水平测试模拟试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项:

1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内。

2．答题时请按要求用笔。

3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5．保持卡面清洁，不要折暴、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．下列命题是真命题的是(　　)

A．平行四边形对角线相等 B．直角三角形两锐角互补

C．不等式﹣2x﹣1＜0的解是x＜﹣ D．多边形的外角和为360°

2．以下运算错误的是（    ）

A． B．

C． D．

3．关于的分式方程有增根，则的值为　　

A．0 B． C． D．

4．如图1，△ABC和△ADE都是等腰直角三角形，∠C和∠ADE都是直角，点C在AE上，△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1，再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图1．两次旋转的角度分别为（　　）

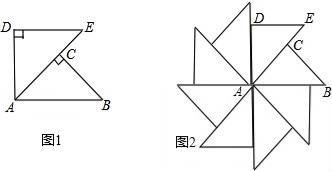
A．45°，90° B．90°，45° C．60°，30° D．30°，60°

5．顺次连结一个平行四边形的各边中点所得四边形的形状是（ ）

A．平行四边形 B．矩形 C．菱形 D．正方形

6．若分式的值为0，则x的值是（　　）

A．2 B．0 C．﹣2 D．任意实数

7．如图,矩形ABCD中,AB=7,BC=4,按以下步骤作图：以点B为圆心,适当长为半径画弧,交AB,BC于点E,F;再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠ABC内部相交于点H,作射线BH,交DC于点G,则DG的长为(     )

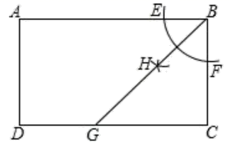
A．1 B．1 C．3 D．2

8．如图，每个小正方形的边长为1，在△ABC中，点D为AB的中点，则线段CD的长为（　　）

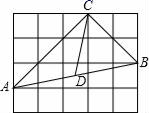
A． B． C． D．

9．如图，四边形ABCD为平行四边形，延长AD到E，使DE＝AD，连接EB，EC，DB，下列条件中，不能使四边形DBCE成为菱形的是（　　）

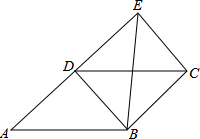
A．AB＝BE B．BE⊥DC C．∠ABE＝90° D．BE平分∠DBC

10．甲、乙、丙、丁四位选手各射击10次，每人的平均成绩都是9.3环，方差如表：

则这四个人种成绩发挥最稳定的是（   ）

A．甲 B．乙 C．丙 D．丁

11．用配方法解方程时，原方程应变形为（  ）

A． B． C． D．

12．如图，CE，BF分别是△ABC的高线，连接EF，EF=6，BC=10，D、G分别是EF、BC的中点，则DG的长为    （    ）

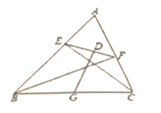
A．6 B．5 C．4 D．3

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，矩形ABCD中，，，将矩形折叠，使点B与点D重合，点A的对应点为，折痕EF的长为________.

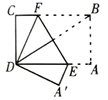
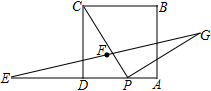
14．如图，正方形ABCD的边长为4，点E为AD的延长线上一点，且DE＝DC，点P为边AD上一动点，且PC⊥PG，PG＝PC，点F为EG的中点．当点P从D点运动到A点时，则CF的最小值为___________

15．若反比例函数y=（2k-1）的图象在二、四象限，则k=________．

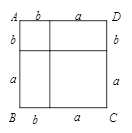
16．如图，正方形ABCD是由两个小正方形和两个小长方形组成的，根据图形写出一个正确的等式：_________.

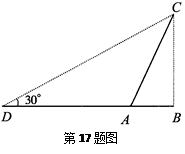
17．如图所示，某人在D处测得山顶C的仰角为30°，向前走200米来到山脚A处，测得山坡AC的坡度i=1∶0.5，则山的高度为____________米.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

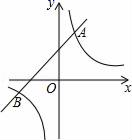
18．（5分）已知一次函数y1=kx+b（k≠0）与反比例函数y2=（m≠0）相交于A和B两点，且A点坐标为（1，1），B点的横坐标为﹣1．

（1）求反比例函数和一次函数的解析式；

（2）根据图象直接写出使得y1＞y2时，x的取值范围．

19．（5分）先化简，再求值：，其中是不等式的正整数解.

20．（8分）阅读下列一段文字，然后回答下列问题．

已知在平面内有两点、，其两点间的距离，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可化简为或.

（1）已知、，试求A、B两点间的距离______.

已知M、N在平行于y轴的直线上，点M的纵坐标为4，点N的纵坐标为-1，试求M、N两点的距离为______；

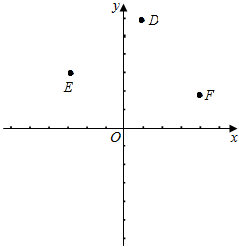
（2）已知一个三角形各顶点坐标为、、，你能判定此三角形的形状吗?说明理由．

（3）在（2）的条件下，平面直角坐标系中，在x轴上找一点P，使的长度最短，求出点P的坐标及的最短长度．

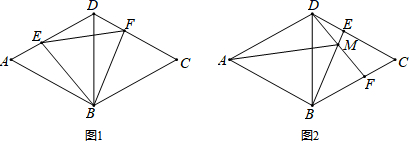
21．（10分）如图，已知菱形ABCD边长为4，，点E从点A出发沿着AD、DC方向运动，同时点F从点D出发以相同的速度沿着DC、CB的方向运动．

如图1，当点E在AD上时，连接BE、BF，试探究BE与BF的数量关系，并证明你的结论；

在的前提下，求EF的最小值和此时的面积；

当点E运动到DC边上时，如图2，连接BE、DF，交点为点M，连接AM，则大小是否变化？请说明理由．

22．（10分）如图，在矩形ABCD中，AC＝60 cm，∠BAC＝60°，点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，同时点F从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点E，F运动的时间是t秒(0<t≤15)．过点F作OF⊥BC于点O，连接OE，EF.

（1）求证：AE＝OF；

（2）四边形AEOF能够成为菱形吗？如果能，求出相应的t值，如果不能，请说明理由；

（3）当t为何值时，△OEF为直角三角形？请说明理由．

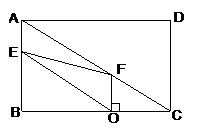
23．（12分）如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交点为 A（-3，0），与y轴交点为B，且与正比例函数的图象的交于点 C（m，4）．

（1）求m的值及一次函数 y=kx+b的表达式；

（2）若点P是y轴上一点，且△BPC的面积为6，请直接写出点P的坐标．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、B

3、D

4、A

5、A

6、A

7、C

8、B

9、A

10、B

11、A

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、

14、

15、1

16、

17、

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）y1=x+2，y2= ；（2）由图象可知y1＞y2时，x＞1或﹣1＜x＜2．

19、1.

20、（1）13，5；（2）等腰直角三角形，理由见解析；（3）当P的坐标为（）时，PD+PF的长度最短，最短长度为.

21、，证明见解析；的最小值是，；如图3，当点E运动到DC边上时，大小不发生变化，理由见解析.

22、（1）证明见解析；（2）能，10；（3）t=或t=12，理由见解析．

23、（1）m的值为3，一次函数的表达式为

（2） 点P的坐标为（0， 6）、（0，－2）