


北京市昌平二中学南校区2022-2023学年七下数学期末质量检测试题含答案
展开北京市昌平二中学南校区2022-2023学年七下数学期末质量检测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项
1.考试结束后,请将本试卷和答题卡一并交回.
2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.
3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.
4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.
5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,在同一平面直角坐标系中,函数![]() 与函数
与函数![]() 的图象大致是( )
的图象大致是( )
A.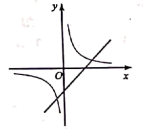 B.
B.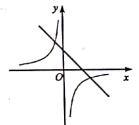
C.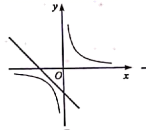 D.
D.
2.如图,在矩形ABCD中,AD=![]() +8,点E在边AD上,连BE,BD平分∠EBC,则线段AE的长是( )
+8,点E在边AD上,连BE,BD平分∠EBC,则线段AE的长是( )
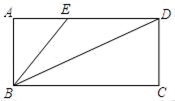
A.2 B.3 C.4 D.5
3.若正比例函数的图象经过点(2,4),则这个图象也必经过点( )
A.(2,1) B.(﹣1,﹣2) C.(1,﹣2) D.(4,2)
4.如图,顺次连接四边形ABCD各边的中点的四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
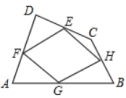
A.AB∥DC B.AC=BD C.AC⊥BD D.AB=CD
5.下列各式中,正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知平行四边形![]() 中,一个内角
中,一个内角![]() ,那么它的邻角
,那么它的邻角![]() ( ).
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.不能判定四边形ABCD是平行四边形的题设是( )
A.AB∥CD,AB=CD B.AB=CD,AD=BC
C.AD=BC,∠A=∠C D.AB∥CD,∠B=∠D
8.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,![]() ,则EC的长是( )
,则EC的长是( )
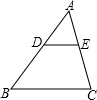
A.4.5 B.8 C.10.5 D.14
9.下列交通标志既是中心对称图形又是轴对称图形的是( )
A. B.
B. C.
C. D.
D.
10.菱形的周长等于其高的8倍,则这个菱形的较大内角是( )
A.30° B.120° C.150° D.135°
11.如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为( )

A.4 B.16 C.2![]() D.4
D.4![]()
12.现定义运算“★”,对于任意实数![]() ,
,![]() ,都有
,都有![]() ,如
,如![]() ,若
,若![]() ,则实数
,则实数![]() 的值为( )
的值为( )
A.-4或-1 B.4或-1 C.4或-2 D.-4或2
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.在平行四边形ABCD中,AE平分![]() 交边BC于E,DF平分
交边BC于E,DF平分![]() 交边BC于F.若
交边BC于F.若![]() ,
,![]() ,则
,则![]() _________.
_________.
14.已知空气的密度是0.001239![]() ,用科学记数法表示为________
,用科学记数法表示为________![]()
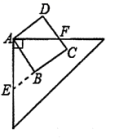
15.边长为![]() 的正方形ABCD与直角三角板如图放置,延长CB与三角板的一条直角边相交于点E,则四边形AECF的面积为________.
的正方形ABCD与直角三角板如图放置,延长CB与三角板的一条直角边相交于点E,则四边形AECF的面积为________.
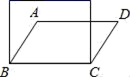
16.如图所示,将四根木条组成的矩形木框变成▱ABCD的形状,并使其面积变为原来的一半,则这个平行四边形的一个最小的内角的度数是_____.
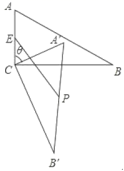
17.如图,在![]() 中,
中,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() ,得到
,得到![]() .设
.设![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ,
,![]() ,连接
,连接![]() ,当
,当![]() ____________
____________![]() 时,
时,![]() 长度最大,最大值为____________.
长度最大,最大值为____________.
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
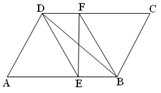
18.(5分)已知:如图,在□ABCD中,DE、BF分别是∠ADC和∠ABC的角平分线,交AB、CD于点E、F,连接BD、EF.
(1)求证:BD、EF互相平分;
(2)若∠A=600,AE=2EB,AD=4,求四边形DEBF的周长和面积.
19.(5分)某村为绿化村道,计划在村道两旁种植 A、B 两种树木,需要购买这两种树苗 800 棵,A、B 两种树苗的相关信息如表:
树苗 | 单价(元/棵) | 成活率 | 植树费(元/棵) |
A | 100 | 80% | 20 |
B | 150 | 90% | 20 |
设购买 A 种树苗 x 棵,绿化村道的总费用为 y 元,解答下列问题:
(1)求出 y 与 x 之间的函数关系式.
(2)若这批树苗种植后成活了 670 棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过 120000 元,则最多可购买 B 种树苗多少棵?
20.(8分) (1)计算:![]() ﹣
﹣![]() ×
×![]()
(2)解方程:x2﹣4x﹣5=0
21.(10分)在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒![]() cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP²、PQ²、CQ² 三者之间的数量关系,请说明理由.

22.(10分)已知一次函数![]() 的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
(1)求一次函数的解析式.
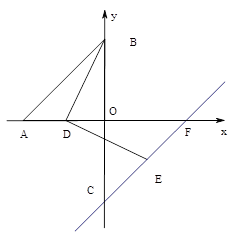
(2)如图,点C与点B关于x轴对称,点D在线段OA上,连结BD,把线段BD顺时针方向旋转90°得到线段DE,作直线CE交x轴于点F,求![]() 的值.
的值.
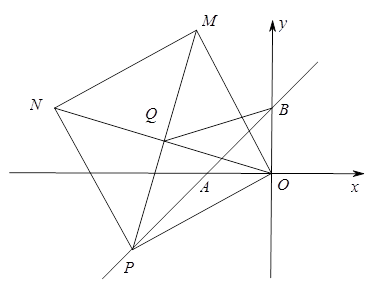
(3)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
23.(12分)关于x的一元二次方程![]() .
.
(1).求证:方程总有两个实数根;
(2).若方程的两个实数根都是正整数,求m的最小值.
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、A
2、B
3、B
4、C
5、B
6、C
7、C
8、B
9、C
10、C
11、A
12、B
二、填空题(每题4分,满分20分,将答案填在答题纸上)
13、4或9
14、1.239×10-3.
15、5
16、30°
17、![]() 3
3
三、解答题 (本大题共7小题,共64分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)证明见解析;(2)四边形DEBF的周长为12 ,面积是4![]()
19、(1)y=—50x+136000;(2)111000 元.(3)若绿化村道的总费用不超过 120000 元,则最多可购买 B 种树苗 1 棵.
20、(1)![]() ;(2)x=﹣1或x=1.
;(2)x=﹣1或x=1.
21、 (1) ![]() ;(1)①v=1;②S=
;(1)①v=1;②S=![]() (3)
(3) ![]()
22、(4)y=x+4.(4)![]() ;(4)不变,
;(4)不变,![]() .
.
23、(1)证明见解析;(2)-1.
北京市昌平二中学南校区2023-2024学年八上数学期末统考模拟试题含答案: 这是一份北京市昌平二中学南校区2023-2024学年八上数学期末统考模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔,若,则 的值为等内容,欢迎下载使用。
北京市昌平区昌平五中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案: 这是一份北京市昌平区昌平五中学2022-2023学年七年级数学第二学期期末教学质量检测模拟试题含答案,共7页。试卷主要包含了考生要认真填写考场号和座位序号,如图,函数y=与y=﹣kx+1,下列条件,将点P,已知一组数据,二次根式中字母a的取值范围是,已知P1等内容,欢迎下载使用。
北京市昌平区北京人大附中昌平校区2022-2023学年数学七下期末调研模拟试题含答案: 这是一份北京市昌平区北京人大附中昌平校区2022-2023学年数学七下期末调研模拟试题含答案,共7页。试卷主要包含了如图,空地上等内容,欢迎下载使用。












