


所属成套资源:【同步学案】苏教版(2019)高中数学 选择性必修第一册 同步导学案
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.1.2 瞬时变化率——导数(1)-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.1.2 瞬时变化率——导数(2)-导学案(有答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.2.2 函数的和、差、积、商的导数-导学案(含答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.2.3 简单复合函数的导数-导学案(含答案) 试卷 0 次下载
- 苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.3.1 单调性(2)-导学案(有答案) 试卷 0 次下载
苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.1.2 瞬时变化率——导数(3)-导学案(有答案)
展开
这是一份苏教版 高中数学 选择性必修第一册 活动单导学课程 第5章导数及其应用5.1.2 瞬时变化率——导数(3)(有答案),共8页。
5.1.2 瞬时变化率——导数(3) ![]() 1. 了解导数的背景,理解导数的概念.2. 通过函数图象直观地理解导数的几何意义.3. 进一步体会建立数学模型刻画客观世界“数学化”的过程,同时又对变量数学的思想方法有新的感悟.
1. 了解导数的背景,理解导数的概念.2. 通过函数图象直观地理解导数的几何意义.3. 进一步体会建立数学模型刻画客观世界“数学化”的过程,同时又对变量数学的思想方法有新的感悟. ![]()
![]() 活动一掌握导数的概念
活动一掌握导数的概念![]() 1. (1) 如何求曲线上任意一点的切线的斜率?(2) 如何求某一时刻物体运动的瞬时速度?(3) 如何求某一时刻物体运动的瞬时加速度? 思考1 以上三个问题有哪些共同特征?(从代数式、求解的目标等进行分析) 2. 导数的定义.思考2 结合上述三个问题探求函数f(x)在x=x0处的导数. 思考3 试从导数的定义,归纳求函数f(x)在x=x0处导数的方法. 思考4 导数f′(x0)的几何意义是什么?
1. (1) 如何求曲线上任意一点的切线的斜率?(2) 如何求某一时刻物体运动的瞬时速度?(3) 如何求某一时刻物体运动的瞬时加速度? 思考1 以上三个问题有哪些共同特征?(从代数式、求解的目标等进行分析) 2. 导数的定义.思考2 结合上述三个问题探求函数f(x)在x=x0处的导数. 思考3 试从导数的定义,归纳求函数f(x)在x=x0处导数的方法. 思考4 导数f′(x0)的几何意义是什么? ![]() 活动二掌握求函数在x=x0处的导数的方法例1 已知f(x)=x2+2.(1) 求f(x)在x=1处的导数f′(1);(2) 求f(x)在x=a处的导数f′(a).
活动二掌握求函数在x=x0处的导数的方法例1 已知f(x)=x2+2.(1) 求f(x)在x=1处的导数f′(1);(2) 求f(x)在x=a处的导数f′(a). ![]() 根据f′(x0)的几何意义及求解过程,体会极限的思想,求得函数f(x)在x=x0处的导数.
根据f′(x0)的几何意义及求解过程,体会极限的思想,求得函数f(x)在x=x0处的导数.![]() 已知f(x)=2x2-x,求f(x)在x=2处的导数.
已知f(x)=2x2-x,求f(x)在x=2处的导数. ![]() 活动三掌握导函数的定义及求法 3. 导函数的定义:若f(x)对于区间(a,b)内任一点都可导,则f(x)在各点处的导数也随着自变量x的变化而变化,因而也是自变量x的函数,该函数称为f(x)的导函数,记作f′(x).导函数f′(x)也简称为f(x)的导数.思考5 “函数f(x)在x=x0处的导数”“导函数”两者之间有哪些区别和联系? 思考6 f′(1) 与f(1) 的含义有什么不同?f′(1) 与f′(x)之间有什么联系? 4. 求导函数:例2 已知f(x)=x2-2x,求 f′(x). 例3 已知f(x)=2x3-1,f′(x0)=6,求x0的值.
活动三掌握导函数的定义及求法 3. 导函数的定义:若f(x)对于区间(a,b)内任一点都可导,则f(x)在各点处的导数也随着自变量x的变化而变化,因而也是自变量x的函数,该函数称为f(x)的导函数,记作f′(x).导函数f′(x)也简称为f(x)的导数.思考5 “函数f(x)在x=x0处的导数”“导函数”两者之间有哪些区别和联系? 思考6 f′(1) 与f(1) 的含义有什么不同?f′(1) 与f′(x)之间有什么联系? 4. 求导函数:例2 已知f(x)=x2-2x,求 f′(x). 例3 已知f(x)=2x3-1,f′(x0)=6,求x0的值. ![]() 活动四掌握导数的几何意义及实际意义 思考7 结合导数的定义,探求在曲线上任意一点的切线的斜率、瞬时速度、瞬时加速度与导数有何联系? 例4 (1) 若曲线y=x2+2ax与直线y=2x-4相切,求a的值;(2) 通过某导体的电量(单位:C)q=2t2+3t,求当t=5 s时的电流强度(单位:A).
活动四掌握导数的几何意义及实际意义 思考7 结合导数的定义,探求在曲线上任意一点的切线的斜率、瞬时速度、瞬时加速度与导数有何联系? 例4 (1) 若曲线y=x2+2ax与直线y=2x-4相切,求a的值;(2) 通过某导体的电量(单位:C)q=2t2+3t,求当t=5 s时的电流强度(单位:A). ![]() 1. 若函数f(x)的图象在x=2处的切线方程是y=-x-1,则f(2)+f′(2)的值为( )A. 0 B. 2 C. -4 D. 42. 已知函数f(x)在R上可导,其部分图象如图所示,设=a,则下列结论中正确的是( )
1. 若函数f(x)的图象在x=2处的切线方程是y=-x-1,则f(2)+f′(2)的值为( )A. 0 B. 2 C. -4 D. 42. 已知函数f(x)在R上可导,其部分图象如图所示,设=a,则下列结论中正确的是( )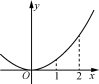 A. f′(1)<f′(2)<aB. f′(1)<a<f′(2)C. f′(2)<f′(1)<aD. a<f′(1)<f′(2)3. (多选)下列命题中,正确的是( )A. 若f′(x0)=0,则函数f(x)在x=x0处无切线B. 函数y=f(x)的切线与函数的图象可以有两个公共点C. 若曲线y=f(x)在x=1处的切线方程为2x-y=0,则 =1D. 若函数f(x)的导数f′(x)=x2-2,且f(1)=2,则f(x)的图象在x=1处的切线方程为x+y-3=04. 已知函数f(x)可导,若 =1,则f′(1)=________.5. 已知f(x)=x3-2,求f′及f′(x).
A. f′(1)<f′(2)<aB. f′(1)<a<f′(2)C. f′(2)<f′(1)<aD. a<f′(1)<f′(2)3. (多选)下列命题中,正确的是( )A. 若f′(x0)=0,则函数f(x)在x=x0处无切线B. 函数y=f(x)的切线与函数的图象可以有两个公共点C. 若曲线y=f(x)在x=1处的切线方程为2x-y=0,则 =1D. 若函数f(x)的导数f′(x)=x2-2,且f(1)=2,则f(x)的图象在x=1处的切线方程为x+y-3=04. 已知函数f(x)可导,若 =1,则f′(1)=________.5. 已知f(x)=x3-2,求f′及f′(x).
参考答案与解析【活动方案】1. 略思考1:代数式都是的形式,其中Δx表示自变量x的改变量,Δy表示相应的函数的改变量.都求的是函数在某一点处的瞬时变化率.思考2:设函数y=f(x)在区间(a,b)上有定义,x0∈(a,b),若Δx无限趋近于0时,比值=无限趋近于一个常数A,则称f(x)在x=x0处可导,并称常数A为函数f(x)在x=x0处的导数,记作f′(x0).思考3:①求函数的增量Δy=f(x0+Δx)-f(x0);②求平均变化率=;③令Δx→0,→A,则A即为函数f(x)在x=x0处的导数,通常也可表示为 =A.思考4:曲线y=f(x)在点(x0,f(x0))处的切线的斜率.例1 (1) 因为===2+Δx,所以当Δx→0时,2+Δx→2,即 = (2+Δx)=2,故f(x)在x=1处的导数为2,即f′(1)=2.(2) 因为===2a+Δx,所以当Δx→0时,2a+Δx→2a,即 = (2a+Δx)=2a,故f(x)在x=a处的导数为2a,即f′(a)=2a.跟踪训练 因为===2Δx+7,所以当Δx→0时,2Δx+7→7,即 = (2Δx+7)=7,故f(x)在x=2处的导数为7.思考5:联系:f(x)在x=x0处的导数f′(x0)就是导函数f′(x)在x=x0处的函数值.区别:导函数是函数,f(x)在x=x0处的导数是数值.思考6:f′(1)表示函数f(x)在x=1处的导数,f(1)表示函数f(x)在x=1处的值,f′(1)表示导函数f′(x)在x=1处的值.例2 因为===Δx+2x-2,所以当Δx→0时,→2x-2,即 = (Δx+2x-2)=2x-2,故f′(x)=2x-2.例3 因为==![]() =6x+6x0(Δx)+2(Δx)2,所以当Δx→0时,→6x,即 =[6x+6x0(Δx)+2(Δx)2]=6x,即f′(x0)=6x.又f′(x0)=6,所以x0=1或x0=-1.思考7:曲线上任一点的切线的斜率、瞬时速度、瞬时加速度即为函数在该点的导数.例4 (1) 因为==2x+2a+Δx, 所以当Δx→0时,→2x+2a,即 = (2x+2a+Δx)=2x+2a,即f′(x)=2x+2a.设切点为(x0,y0),则2x0+2a=2,y0=2x0-4=x+2ax0,解得x0=±2.当x0=2时,a=-1;当x0=-2时,a=3.(2) 因为==4t+3+2Δt,所以当Δt→0时,→4t+3,即 = (4t+3+2Δt)=4t+3,即q′=4t+3,故当t=5 s时,电流强度为23A.【检测反馈】1. C 解析:因为函数f(x)的图象在x=2处的切线方程是y=-x-1,所以f(2)=-2-1=-3,f′(2)=-1,所以f(2)+f′(2)=-4.2. B 解析:由图象可知,当x>0时,函数的增长越来越快,故函数图象切线的斜率越来越大.因为=a,易知f′(1)<a<f′(2).3. BD 解析:若f′(x0)=0,则函数f(x)在x=x0处的切线斜率为0,存在切线,故A错误;如函数f(x)=x3-3x在x=1处的切线为y=-2,与函数的图象还有一个公共点(-2,-2),故B正确;因为曲线y=f(x)在x=1处的切线方程为2x-y=0,所以f′(1)=2.又 =- =-f′(1)=-1≠1,故C错误;因为函数f(x)的导数f′(x)=x2-2,所以f′(1)=12-2=-1.又f(1)=2,所以切点坐标为(1,2),切线的斜率为-1,所以切线方程为y-2=-(x-1),即x+y-3=0,故D正确.故选BD. 4. 3 解析:因为 =1,即· =1,所以f′(1)=1,故f′(1)=3.5. 因为==2x2+2x(Δx)+(Δx)2,所以当Δx→0时,→2x2,即 =2x2,即f′(x)=2x2.当x=-时,f′=.
=6x+6x0(Δx)+2(Δx)2,所以当Δx→0时,→6x,即 =[6x+6x0(Δx)+2(Δx)2]=6x,即f′(x0)=6x.又f′(x0)=6,所以x0=1或x0=-1.思考7:曲线上任一点的切线的斜率、瞬时速度、瞬时加速度即为函数在该点的导数.例4 (1) 因为==2x+2a+Δx, 所以当Δx→0时,→2x+2a,即 = (2x+2a+Δx)=2x+2a,即f′(x)=2x+2a.设切点为(x0,y0),则2x0+2a=2,y0=2x0-4=x+2ax0,解得x0=±2.当x0=2时,a=-1;当x0=-2时,a=3.(2) 因为==4t+3+2Δt,所以当Δt→0时,→4t+3,即 = (4t+3+2Δt)=4t+3,即q′=4t+3,故当t=5 s时,电流强度为23A.【检测反馈】1. C 解析:因为函数f(x)的图象在x=2处的切线方程是y=-x-1,所以f(2)=-2-1=-3,f′(2)=-1,所以f(2)+f′(2)=-4.2. B 解析:由图象可知,当x>0时,函数的增长越来越快,故函数图象切线的斜率越来越大.因为=a,易知f′(1)<a<f′(2).3. BD 解析:若f′(x0)=0,则函数f(x)在x=x0处的切线斜率为0,存在切线,故A错误;如函数f(x)=x3-3x在x=1处的切线为y=-2,与函数的图象还有一个公共点(-2,-2),故B正确;因为曲线y=f(x)在x=1处的切线方程为2x-y=0,所以f′(1)=2.又 =- =-f′(1)=-1≠1,故C错误;因为函数f(x)的导数f′(x)=x2-2,所以f′(1)=12-2=-1.又f(1)=2,所以切点坐标为(1,2),切线的斜率为-1,所以切线方程为y-2=-(x-1),即x+y-3=0,故D正确.故选BD. 4. 3 解析:因为 =1,即· =1,所以f′(1)=1,故f′(1)=3.5. 因为==2x2+2x(Δx)+(Δx)2,所以当Δx→0时,→2x2,即 =2x2,即f′(x)=2x2.当x=-时,f′=.







