2022-2023学年浙江省玉环市七下数学期末经典试题含答案

2022-2023学年浙江省玉环市七下数学期末经典试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．剪纸艺术是中国传统的民间工艺．下列剪纸的图案中，属于中心对称图形的是（    ）

A． B． C． D．

2．直角三角形两条直角边分别是和，则斜边上的中线等于（    ）

A． B．13 C．6 D．

3．若正比例函数的图象经过点（，2），则这个图象必经过点（ ）．

A．（1，2） B．（，） C．（2，） D．（1，）

4．一次函数y＝ax＋1与y＝bx－2的图象交于x轴上同一个点，那么a∶b的值为(　　)

A．1∶2    B．－1∶2    C．3∶2    D．以上都不对

5．在△ABC中，∠C＝90°，AB＝c，∠A＝30°，则AC＝（　　）

A．c B．c C．2c D．c

6．张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子（x＞0）的最小值是1”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是，矩形的周长是1（）；当矩形成为正方形时，就有x=（x＞0），解得x=1，这时矩形的周长1（）=4最小，因此（x＞0）的最小值是1．模仿张华的推导，你求得式子（x＞0）的最小值是（ ）

A．1 B．1 C．6 D．10

7．下列给出的条件中不能判定一个四边形是矩形的是(    )

A．一组对边平行且相等，一个角是直角

B．对角线互相平分且相等

C．有三个角是直角

D．一组对边平行，另一组对边相等，且对角线相等

8．直角三角形中，两直角边分别是12和5，则斜边上的中线长是（    ）

A．13 B．9 C．8.5 D．6.5

9．分式方程的解为（  ）

A． B． C． D．

10．下列说法正确的是（   ）

A．明天会下雨是必然事件

B．不可能事件发生的概率是0

C．在水平的桌面上任意抛掷一枚图钉，一定针尖向下

D．投掷一枚之地近月的硬币1000次，正面朝下的次数一定是500次

11．如图，点E在正方形ABCD内，满足∠AEB=90°，AE=3，BE=4，则阴影部分的面积是（  ）

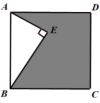
A．12 B．16 C．19 D．25

12．将一个n边形变成(n＋1)边形，内角和将(　　)

A．减少180° B．增加90°

C．增加180° D．增加360°

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．若二次根式有意义，则x的取值范围是　 ▲  ．

14．已知△ABC的周长为4，顺次连接△ABC三边的中点构成的新三角形的周长为__________．

15．设m，n分别为一元二次方程x2+2x﹣2018=0的两个实数根，则m2+3m+n=______．

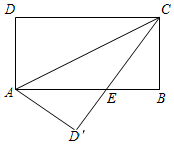
16．如图，在矩形ABCD中，，，将矩形沿AC折叠，则重叠部分的面积为______．

17．已知一次函数的图象经过第一、二、四象，请你写出一个满足条件的值__________.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）甲乙两位同学参加数学综合素质测试，各项成绩如下表：（单位：分）

（1）分别计算甲、乙同学成绩的中位数；

（2）如果数与代数，空间与图形，统计与概率，综合与实践的成绩按4：3：1：2计算，那么甲、乙同学的数学综合素质成绩分别为多少分？

19．（5分）某校在一次广播操比赛中，甲、乙、丙各班得分如下表：

（1）根据三项得分的平均分，从高到低确定三个班级排名顺序．

（2）该校规定：服装统一、动作整齐、动作准确三项得分都不得低于80分，并按，，的比例计入总分根据规定，请你通过计算说明哪一组获得冠军．

20．（8分）如图，在平面直角坐标系中，一次函数y=kx+b的图象经过点A（-2，6），且与x轴交于点B，与正比例函数y=3x的图象相交于点C，点C的横坐标是1．

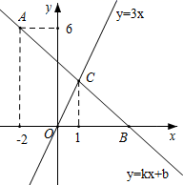
（1）求此一次函数的解析式；

（2）请直接写出不等式（k-3）x+b＞0的解集；

（3）设一次函数y=kx+b的图象与y轴交于点M，点N在坐标轴上，当△CMN是直角三角形时，请直接写出所有符合条件的点N的坐标．

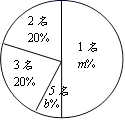
21．（10分）为了有效地落实国家精准扶贫政策，切实关爱贫困家庭学生．某校对全校各班贫困家庭学生的人数情况进行了调查．发现每个班级都有贫困家庭学生，经统计班上贫困家庭学生人数分别有1名、2名、3名、5名，共四种情况，并将其制成了如下两幅不完整的统计图：

(1)填空：a =          ，b=          ；

(2)求这所学校平均每班贫困学生人数；

(3)某爱心人士决定从2名贫困家庭学生的这些班级中，任选两名进行帮扶，请用列表或画树状图的方法，求出被选中的两名学生来自同一班级的概率．

22．（10分）如图1，的所对边分别是，且，若满足，则称为奇异三角形，例如等边三角形就是奇异三角形.

（1）若，判断是否为奇异三角形，并说明理由；

（2）若，，求的长；

（3）如图2，在奇异三角形中，，点是边上的中点，连结，将分割成2个三角形，其中是奇异三角形，是以为底的等腰三角形，求的长.

23．（12分）甲、乙两人参加射箭比赛，两人各射了5箭，他们的成绩（单位：环）统计如下表.

（1）分别计算甲、乙两人射箭比赛的平均成绩；

（2）你认为哪个人的射箭成绩比较稳定?为什么?

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、D

2、A

3、D

4、B

5、B

6、C

7、D

8、D

9、C

10、B

11、C

12、C

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、．

14、2

15、2016

16、1

17、答案不唯一

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）甲的中位数91.5，乙的中位数93；（2）甲的数学综合成绩92，乙的数学综合成绩91.1.

19、（1）乙、甲、丙；（2）丙班级获得冠军．

20、（1）y=-x+4；（2）x＜1；（3）当△CMN是直角三角形时，点N的坐标为（-4，0），（0，2），（-2，0），（0，3）．

21、 (1) a=2，b=10；(2)2;(3).

22、（1）是，理由见解析；（2）；（3）

23、（1）甲：6；乙：6；（2）乙更稳定