


2022-2023学年浙江省台州市坦头中学七下数学期末学业质量监测试题含答案
展开2022-2023学年浙江省台州市坦头中学七下数学期末学业质量监测试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。不按以上要求作答无效。
4.考生必须保证答题卡的整洁。考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.已知![]() 是正比例函数,则m的值是( )
是正比例函数,则m的值是( )
A.8 B.4 C.±3 D.3
2.如图,将平行四边形纸片![]() 折叠,使顶点
折叠,使顶点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,折痕为
处,折痕为![]() ,那么对于结论:①
,那么对于结论:①![]() ,②
,②![]() .下列说法正确的是( )
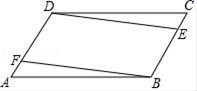
.下列说法正确的是( )
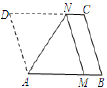
A.①②都错 B.①对②错 C.①错②对 D.①②都对
3.已知四边形ABCD是任意四边形,若在下列条件中任取两个,使四边形ABCD是平行四边形,①AB∥CD;②BC∥AD,③AB=CD;④BC=AD,则符合条件的选择有( )
A.2组 B.3组 C.4组 D.6组
4.经过多边形一个角的两边剪掉这个角,则得到的新多边形的外角和( )
A.比原多边形多![]() B.比原多边形少
B.比原多边形少![]() C.与原多边形外角和相等 D.不确定
C.与原多边形外角和相等 D.不确定
5.如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连接EG、OF,下列四个结论:①CE=CB;②AE=![]() OE;③OF=
OE;③OF=![]() CG,其中正确的结论只有( )
CG,其中正确的结论只有( )
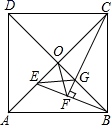
A.①②③ B.②③ C.①③ D.①②
6.若菱形的周长为16,高为2,则菱形两个邻角的比为( )
A.6:1 B.5:1 C.4:1 D.3:1
7.为了解某公司员工的年工资情况,小明随机调查了10位员工,其年工资如下![]() 单位:万元
单位:万元![]() :4,4,4,5,6,6,7,7,9,
:4,4,4,5,6,6,7,7,9,![]() 则下列统计量中,能合理反映该公司员工年工资中等水平的是
则下列统计量中,能合理反映该公司员工年工资中等水平的是![]()
![]()
A.平均数 B.中位数 C.众数 D.方差
8.菱形的边长是2cm,一条对角线的长是2![]() cm,则另一条对角线的长是( )
cm,则另一条对角线的长是( )
A.4 cm B.![]() cm C.2 cm D.2
cm C.2 cm D.2![]() cm
cm
9.生物学家发现:生物具有遗传多样性,遗传密码大多储存在![]() 分子上.一个
分子上.一个![]() 分子的直径约为0.0000002
分子的直径约为0.0000002![]() ,这个数用科学计数法可以表示为( )
,这个数用科学计数法可以表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.下列图形中既是中心对称图形又是轴对称图形的是
A. B.
B. C.
C. D.
D.
二、填空题(本大题共有6小题,每小题3分,共18分)
11.列不等式:据中央气象台报道,某日我市最高气温是33℃,最低气温是25℃,则当天的气温t(℃)的变化范围是______.
12.如图是由6个形状大小完全相同菱形组成的网格,若菱形的边长为1,一个内角(∠O)为60°,△ABC的各顶点都在格点上,则BC边上的高为______.
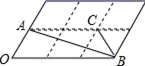
13.如图,直线y=![]() x+1与坐标轴相交于A、B两点,在其图象上取一点A1,以O、A1为顶点作第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样作下去,则第10个等边三角形的边长为_____.
x+1与坐标轴相交于A、B两点,在其图象上取一点A1,以O、A1为顶点作第一个等边三角形OA1B1,再在直线上取一点A2,以A2、B1为顶点作第二个等边三角形A2B1B2,…,一直这样作下去,则第10个等边三角形的边长为_____.
14.数据2,0,1,9,0,6,1,6的中位数是______.
15.一次函数![]() 与
与![]() 轴的交点是__________.
轴的交点是__________.
16.在一个不透明的袋子里装有3个白色乒乓球和若干个黄色乒乓球,若从这个袋子里随机摸出一个乒乓球,恰好是黄球的概率为0.7,则袋子内共有乒乓球__________个。
三、解下列各题(本大题共8小题,共72分)
17.(8分)如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:
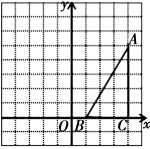
(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求在平移过程中线段AB扫过的面积.
18.(8分)一家水果店以每千克2元的价格购进某种水果若干千克,然后以每千克4元的价格出售,每天可售出100千克,通过调查发现,这种水果每千克的售价每降低1元,每天可多售出200千克.
(1)若将这种水果每千克的售价降低![]() 元,则每天销售量是多少千克?(结果用含
元,则每天销售量是多少千克?(结果用含![]() 的代数式表示)
的代数式表示)
(2)若想每天盈利300元,且保证每天至少售出260千克,那么水果店需将每千克的售价降低多少元?
19.(8分)如图,方格纸中的每个小方格都是边长为1个单位长度的小正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A,B,C三点的坐标分别为(5,﹣1),(2,﹣5),(2,﹣1).
(1)把△ABC向上平移6个单位后得到△A1B1C1,画出△A1B1C1;
(2)画出△A2B2C2,使它与△ABC关于y轴对称;
(3)画出△A3B3C3,使它与△ABC关于原点中心对称.
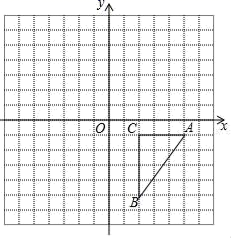
20.(8分)已知E、F分别是平行四边形ABCD的BC和DA边上的点,且CE=AF,问:DE与FB是否平行?说明理由.
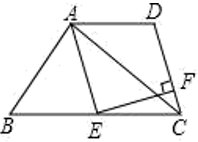
21.(8分)如图,在四边形ABCD中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
(1)求证:四边形AECD是菱形;
(2)若AB=5,AC=12,求EF的长.
22.(10分)在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
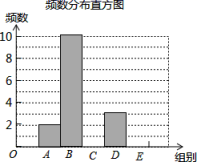
请根据以上信息解答下列问题:
(1)填空:m= ______ ,n= ______ ;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
23.(10分)解方程:
(1)x2-3x+1=1;
(2)x(x+3)-(2x+6)=1.
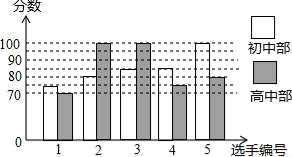
24.(12分)某学校举行“中国梦,我的梦”演讲比赛,初、高中部根据初赛成绩,各选出5名选手组成代表队决赛,初、高中部代表队的选手决赛成绩如图所示:
(1)根据图示填写表格:
| 平均数(分) | 中位数(分) | 众数(分) |
初中代表队 | 85 |
| 85 |
高中代表队 |
| 80 |
|
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、D
3、C
4、C
5、A
6、B
7、B
8、C
9、B
10、B
二、填空题(本大题共有6小题,每小题3分,共18分)
11、25≤t≤1.
12、![]()
13、![]()
14、1.2
15、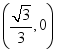
16、10
三、解下列各题(本大题共8小题,共72分)
17、(1)图见解析,![]() ;(2)25
;(2)25
18、(1)每天销售量是![]() 千克;(2)水果店需将每千克的售价降低1元.
千克;(2)水果店需将每千克的售价降低1元.
19、 (1)见解析;(2)见解析;(3)见解析.
20、DE∥FB
21、(1)证明见解析;(2)![]() .
.
22、(1)4;1;(2)见解析;(3)B;(4)48.
23、(4)x4=![]() ,x2=
,x2=![]() ;(2)x4=-3,x2=2.
;(2)x4=-3,x2=2.
24、(1)详见解析;(2)初中部成绩好些
2023-2024学年浙江省台州市坦头中学八上数学期末质量跟踪监视试题含答案: 这是一份2023-2024学年浙江省台州市坦头中学八上数学期末质量跟踪监视试题含答案,共8页。试卷主要包含了考生必须保证答题卡的整洁,16的平方根是,下列命题中,属于假命题的是等内容,欢迎下载使用。
浙江省宁波市江北中学2022-2023学年数学七下期末学业质量监测试题含答案: 这是一份浙江省宁波市江北中学2022-2023学年数学七下期末学业质量监测试题含答案,共7页。
浙江省台州市坦头中学2022-2023学年七下数学期末经典试题含答案: 这是一份浙江省台州市坦头中学2022-2023学年七下数学期末经典试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁,下列各式中,属于分式的是,下列说法中,错误的是等内容,欢迎下载使用。












