2022-2023学年浙江省宁波市奉化区溪口中学数学七下期末统考试题含答案

2022-2023学年浙江省宁波市奉化区溪口中学数学七下期末统考试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

请考生注意：

1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题(每小题3分,共30分)

1．有100个数据，落在某一小组内的频数与总数之比是0.4，那么在这100个数据中，落在这一小组内的数据的频数是（　　）

A．100    B．40    C．20    D．4

2．如图，已知正方形面积为36平方厘米,圆与各边相接，则阴影部分的面积是（   ）平方厘米.（）

A．18 B．7.74 C．9 D．28.26

3．在以下列三个数为边长的三角形中，不能组成直角三角形的是（　　）

A．4、7、9 B．5、12、13 C．6、8、10 D．7、24、25

4．下列函数中，是正比例函数的是(     )

A． B． C． D．

5．在平面直角坐标系xOy中，线段AB的两个端点坐标分别为A(-1，-1)，B(1，2)，平移线段AB得到线段A’B’（点A与A’对应），已知A’的坐标为(3，-1)，则点B’的坐标为(  )

A．(4，2) B．(5，2) C．(6，2) D．(5，3)

6．下列各式从左到右的变形是因式分解的是　　

A． B．

C． D．

7．如图，第一个图形中有4个“”，第二个图形中有7个“”，第三个图形中有11个“”，按照此规律下去，第8个图形中“”的个数为（   ）.

A．37 B．46 C．56 D．67

8．如图，在矩形ABCD中，AB=2，AD=3，E是BC边上一点，将沿AE折叠，使点B落在点处，连接，则的最小值是（    ）

A． B． C． D．

9．如图，点O（0，0），A（0，1）是正方形OAA1B的两个顶点，以正方形的对角线OA1为边作正方形OA1A2B1，再以正方形的对角线OA2为边作正方形OA1A2B1，…，依此规律，则点A2017的坐标是（　　）

A．（21008，0） B．（21008，﹣21008） C．（0，21010） D．（22019，﹣22019）

10．在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是（　　）

A．测量对角线，看是否互相平分

B．测量两组对边，看是否分别相等

C．测量对角线，看是否相等

D．测量对角线的交点到四个顶点的距离，看是否都相等

二、填空题(本大题共有6小题，每小题3分，共18分)

11．已知y是x的一次函数下表列出了部分对应值，则m=_______

12．关于x的一元二次方程（x+1）（x+7）= -5的根为_______________．

13．在一次身体的体检中，小红、小强、小林三人的平均体重为42kg，小红、小强的平均体重比小林的体重多6kg，小林的体重是___kg．

14．将直线向上平移3个单位长度与直线重合，则直线的解析式为__________．

15．已知三角形的三条中位线的长分别为5cm、6cm、10cm，则这个三角形的周长是_____cm．

16．二次根式中，x的取值范围是________．

三、解下列各题(本大题共8小题，共72分)

17．（8分）某商店准备进一批季节性小家电，单价40元．经市场预测，销售定价为52元时，可售出180个，定价每增加1元，销售量净减少10个；定价每减少1元，销售量净增加10个．因受库存的影响，每批次进货个数不得超过180个，商店若将准备获利2000元，则应进货多少个？定价为多少元？

18．（8分）.某酒厂生产A，B两种品牌的酒，平均每天两种酒共可售出600瓶，每种酒每瓶的成本和售价如表所示，设平均每天共获利y元，平均每天售出A种品牌的酒x瓶.

（1）请写出y关于x的函数关系式；

（2）如果该厂每天至少投入成本25000元，且售出的B种品牌的酒不少于全天销售总量的55%，那么共有几种销售方案?并求出每天至少获利多少元?

19．（8分）观察下列各式

，

，

，

，

由此可推断

（1）＝　   　＝　   　．

（2）请猜想（1）的特点的一般规律，用含m的等式表示出来为　   　＝　   　（m表示正整数）．

（3）请参考（2）中的规律计算：

20．（8分）某加工车间共有20名工人，现要加工1800个甲种零件，1000 个乙种零件，已知每人每天加工甲种零件30个或乙种零件50个(每人只能加工一种零件),怎样分工才能确保同时完成两种零件的加工任务?

21．（8分）已知A(n，-2)，B(1，4)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点，直线AB与y轴交于点C．

  (1)求反比例函数和一次函数的关系式；

  (2)求△AOC的面积；

  (3)求不等式kx+b-<0的解集(直接写出答案)．

22．（10分）已知正方形中，为对角线上一点，过点作交于点，连接，为的中点，连接．

（1）如图1，求证：；

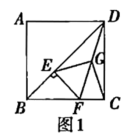
（2）将图1中的绕点逆时针旋转45°，如图2，取的中点，连接．问（1）中的结论是否仍然成立？若成立，给出证明；若不成立，请说明理由．

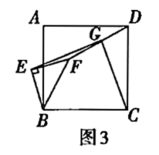
（3）将图1中的绕点逆时计旋转任意角度，如图3，取的中点，连接．问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）

23．（10分）（阅读理解）

对于任意正实数、，∵，

∴

∴，只有当时，等号成立．

（数学认识）

在（、均为正实数）中，若为定值，则，只有当时，有最小值．

（解决问题）

（1）若时，当_____________时，有最小值为_____________；

（2）如图，已知点在反比例函数的图像上，点在反比例函数的图像上，轴，过点作轴于点，过点作轴于点．求四边形周长的最小值．

24．（12分）如图，过点A（2，0）的两条直线，分别交y轴于B，C，其中点B在原点上方，点C在原点下方，已知AB=.

（1）求点B的坐标；

（2）若△ABC的面积为4，求的解析式．

参考答案

一、选择题(每小题3分,共30分)

1、B

2、B

3、A

4、B

5、B

6、C

7、B

8、A

9、B

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、1

12、

13、1.

14、

15、1

16、

三、解下列各题(本大题共8小题，共72分)

17、该商品每个定价为1元，进货100个.

18、（1）y；（2）共有4种方案，10335.

19、（1），；（2） ，；（3）0.

20、安排15名工人加工甲种零件，5名工人加工乙种零件．

21、 (1)反比例函数关系式：；一次函数关系式：y=1x+1;(1) 3；（3）x<-1或0<x<1.

22、 (1)见解析;(2)见解析;(3)见解析.

23、（1）1,1；（1）2.

24、（1）（0，3）；（2）．