2022-2023学年河北省石家庄创新国际学校七下数学期末综合测试试题含答案

2022-2023学年河北省石家庄创新国际学校七下数学期末综合测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

考生请注意：

1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。考试结束后，请将本试卷和答题卡一并交回。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．三角形两边长分别为2和4，第三边是方程x2－6x+8=0的解，则这个三角形的周长是（ ）．

A．8 B．8或10 C．10 D．8和10

2．在平行四边形ABCD中，∠A=110°，∠B=70°，则∠C的度数是（     ）

A．70° B．90° C．110° D．130°

3．一元二次方程x2﹣4x﹣6＝0经过配方可变形为（　　）

A．（x﹣2）2＝10 B．（x+2）2＝10 C．（x﹣4）2＝6 D．（x﹣2）2＝2

4．如图，在周长为 18cm 的▱ABCD 中，AC、BD 相交于点 O,OE⊥BD 交 AD 于 E，则△ABE的周长为（    ）

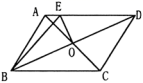
A．6cm B．7cm

C．8cm D．9cm

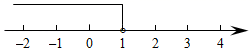
5．的取值范围如数轴所示，化简的结果是（    ）

A． B． C． D．

6．下列计算结果正确的是　　

A． B． C． D．

7．若关于的不等式组有三个整数解，且关于的分式方程有整数解，则满足条件的所有整数的和是（   ）

A． B． C． D．

8．如图所示，梯子AB靠在墙上，梯子的底端A到墙根O的距离为2m，梯子顶端B到地面距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于4m，同时梯子的顶端B下降至B′，那么BB′的长为（　　）

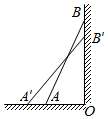
A．等于1m B．大于1m C．小于1m D．以上答案都不对

9．如果一个正多边形的中心角为60°，那么这个正多边形的边数是（   ）

A．4 B．5 C．6 D．7

10．小明在画函数（＞0）的图象时，首先进行列表，下表是小明所列的表格，由于不认真列错了一个不在该函数图象上的点，这个点是

A． B． C． D．

11．下列图标中，是中心对称图形的是（　　）

A． B．

C． D．

12．下列各命题的逆命题成立的是（  ）

A．全等三角形的对应角相等 B．若两数相等，则它们的绝对值相等

C．若两个角是45，那么这两个角相等 D．两直线平行，同位角相等

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13．如图，在直角坐标系中，A、B两点的坐标分别为(0，8)和(6，0)，将一根橡皮筋两端固定在A、B两点处，然后用手勾住橡皮筋向右上方拉升，使橡皮筋与坐标轴围成一个矩形AOBC，则橡皮筋被拉长了_____个单位长度．

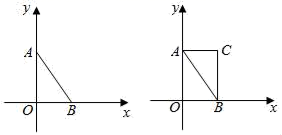
14．已知点P（a+3，7+a）位于二、四象限的角平分线上，则点P的坐标为_________________.

15．一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：

点到直线的距离公式是：

如：求：点到直线的距离．

解：由点到直线的距离公式，得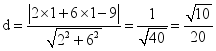

根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．

则两条平行线：和：间的距离是______．

16．观察下列各式，并回答下列问题：

①；②；③；……

（1）写出第④个等式：________；

（2）将你猜想到的规律用含自然数的代数式表示出来，并证明你的猜想.

17．若代数式的值比的值大3，则的值为______.

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18．（5分）观察下列等式：

，

将以上二个等式两边分别相加得：

用你发现的规律解答下列总是：

（1）直接写出下列各式的计算结果：

①_______________________

②______________________

（2）仿照题中的计算形式，猜想并写出：___________________________

（3）解方程：

19．（5分）如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB的角平分线于点E，交∠ACB的外角平分线于点F

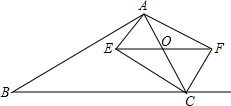
（1）求证：EO＝FO；

（2）当点O运动到何处时，四边形CEAF是矩形？请证明你的结论．

（3）在第（2）问的结论下，若AE＝3，EC＝4，AB＝12，BC＝13，请直接写出凹四边形ABCE的面积为　   　．

20．（8分）先化简，再求值：，其中a＝+1．

21．（10分）某河流防污治理工程已正式启动，由甲队单独做5个月后，乙队再加入合作3个月就可以完成这项工程。已知若甲队单独做需要10个月可以完成。

（1）乙队单独完成这项工程需要几个月？

（2）已知甲队每月施工费用为15万元，比乙队多6万元，按要求该工程总费用不超过141万元，工程必须在一年内竣工（包括12个月）．为了确保经费和工期，采取甲队做a个月，乙队做b个月（a、b均为整数）分工合作的方式施工，问有哪几种施工方案？

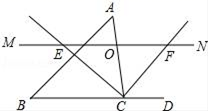
22．（10分）如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

（1）求证：OE＝OF；

（2）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

23．（12分）如图，图1、图2是两张大小完全相同的6×6方格纸，每个小方格的顶点叫做格点，以格点为顶点的多边形叫做格点多边形．网格中有一个边长为2的格点正方形，按下列要求画出拼图后的格点平行四边形（用阴影表示） 

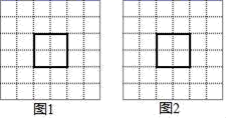
（1）把图1中的格点正方形分割成两部分，再通过图形变换拼成一个平行四边形，在图1中画出这个格点平行四边形；   

（2）把图2中的格点正方形分割成三部分，再通过图形变换拼成一个平行四边形，在图2中画出这个格点平行四边形．

参考答案

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1、C

2、C

3、A

4、D

5、D

6、C

7、B

8、C

9、C

10、D

11、B

12、D

二、填空题（每题4分，满分20分，将答案填在答题纸上）

13、1

14、 (-2,2)

15、

16、（1）；（2）猜想：

17、1或2；

三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）

18、（1）①；②；（2）；（3）.

19、（1）详见解析；（2）当点O运动到AC的中点时，四边形CEAF是矩形，理由详见解析；（3）1．

20、

21、（1）15（2）方案一：甲队作4个月，乙队作9个月；方案二：甲队作2个月，乙队作1个月

22、（1）证明见解析；（2）当点O在边AC上运动到AC中点时，四边形AECF是矩形，理由见解析．

23、（1）见解析；（2）见解析