


2022-2023学年江西省鄱阳县七下数学期末学业质量监测模拟试题含答案
展开2022-2023学年江西省鄱阳县七下数学期末学业质量监测模拟试题
(时间:120分钟 分数:120分)
学校_______ 年级_______ 姓名_______
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题(每小题3分,共30分)
1.下列说法,你认为正确的是( )
A.0 的倒数是 0 B.3-1=-3 C.是有理数 D.![]() 3
3
2.三角形的三边长为![]() ,则这个三角形是( )
,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
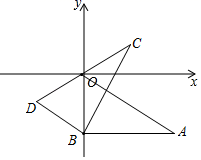
3.Rt△ABO与Rt△CBD在平面直角坐标系中的位置如图所示,∠ABO=∠CBD=90°,若点A(2![]() ,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
,﹣2),∠CBA=60°,BO=BD,则点C的坐标是( )
A.(2,2![]() ) B.(1,
) B.(1,![]() ) C.(
) C.(![]() ,1) D.(2
,1) D.(2![]() ,2)
,2)
4.若一次函数y=x+4的图象上有两点A(﹣![]() ,y1)、B(1,y2),则下列说法正确的是( )
,y1)、B(1,y2),则下列说法正确的是( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
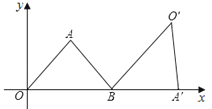
5.如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A.(![]() ,
,![]() ) B.(
) B.(![]() ,
,![]() ) C.(
) C.(![]() ,
,![]() ) D.(
) D.(![]() ,4
,4![]() )
)
6.对于抛物线y=﹣(x+2)2﹣1,下列说法错误的是( )
A.开口向下
B.对称轴是直线x=﹣2
C.x>﹣2时,y随x的增大而增大
D.x=﹣2,函数有最大值y=﹣1
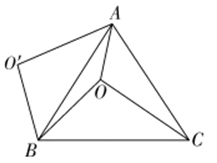
7.如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转
为旋转中心逆时针旋转![]() 得到线段
得到线段![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到;②点
得到;②点![]() 与点
与点![]() 的距离为8;③
的距离为8;③![]() ;④
;④![]() ;其中正确的结论是( )
;其中正确的结论是( )
A.①②③ B.①③④ C.②③④ D.①②
8. 观察下列四个平面图形,其中是中心对称图形的个数是( )

A.1个 B.2个 C.3个 D.4个
9.在解分式方程![]() +
+![]() =2时,去分母后变形正确的是( )
=2时,去分母后变形正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.下列说法中,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是矩形
D.对角线互相垂直的平行四边形是矩形
二、填空题(本大题共有6小题,每小题3分,共18分)
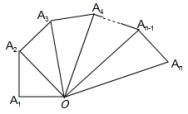
11.如图,OA1=A1A2=A2A3=A3A4=…=An-1An=1,∠OA1A2=∠OA2A3=∠OA3a4=…=∠OAn-1An=90°(n>1,且n为整数).那么OA2=_____,OA4=______,…,OAn=_____.
12.将一元二次方程![]() 化成一般式后,其一次项系数是______.
化成一般式后,其一次项系数是______.
13.已知点M(m,3)在直线![]() 上,则m=______.
上,则m=______.
14.己知一个菱形的边长为2,较长的对角线长为2![]() ,则这个菱形的面积是_____.
,则这个菱形的面积是_____.
15.若分式![]() 的值为0,则x的值为_______.
的值为0,则x的值为_______.
16.命题“如果a2=b2,那么a=b.”的否命题是__________.
三、解下列各题(本大题共8小题,共72分)
17.(8分)某汽车租凭公司要购买轿车和面包车共![]() 辆,其中轿车最少要购买
辆,其中轿车最少要购买![]() 辆,轿车每辆
辆,轿车每辆![]() 万元,购头面包车每辆
万元,购头面包车每辆![]() 万元,公司可投入的购车资金不超过
万元,公司可投入的购车资金不超过![]() 万元.
万元.
(1)符合公司要求的购买方案有几种?请说明理由;
(2)如果每辆轿车日租金为![]() 元,每辆面包车日租金为
元,每辆面包车日租金为![]() 元,假设新购买的这
元,假设新购买的这![]() 辆汽车每日都可以全部租出,公司希望
辆汽车每日都可以全部租出,公司希望![]() 辆汽车的日租金最高,那么应该选择以上的哪种购买方案?且日租金最高为多少元?
辆汽车的日租金最高,那么应该选择以上的哪种购买方案?且日租金最高为多少元?
18.(8分)阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,t2=81,∴t=±1因为2m2+n2≥0,所以2m2+n2=1.
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
已知实数x,y满足(4x2+4y2+3)(4x2+4y2﹣3)=27,求x2+y2的值.
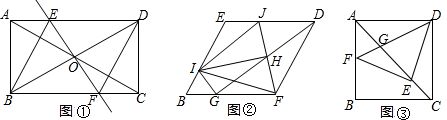
19.(8分) (1)如图①,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,交AD于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数;
(2)把(1)中菱形BFDE进行分离研究,如图②,点G、I分别在BF、BE边上,且BG=BI,连接GD,H为GD的中点,连接FH并延长,交ED于点J,连接IJ、IH、IF、IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图③,当矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE、EF、DF,使△DEF是等腰直角三角形,DF交AC于点G.请直接写出线段AG、GE、EC三者之间满足的数量关系.
20.(8分)为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
画出频数分布直方图,如下:
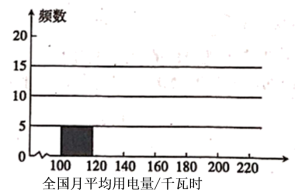
(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
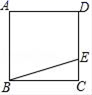
21.(8分)在正方形ABCD中,E是CD上的点.若BE=30,CE=10,求正方形ABCD的面积和对角线长.
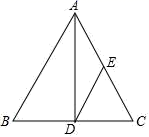
22.(10分)如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为24,求BC的长度.
23.(10分)为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() (无满分),将其按分数段分为五组,绘制出以下不完整表格:
(无满分),将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 |
|
二 |
| 10 | 0.2 |
三 |
| 12 |
|
四 |
|
| 0.4 |
五 |
| 6 |
|
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有__________名学生参加;
(2)直接写出表中:![]() ___________
___________![]() ____________
____________
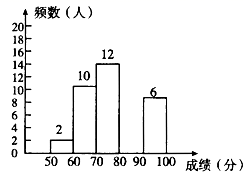
(3)请补全右面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为__________.
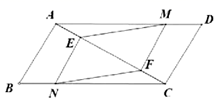
24.(12分)如图,在![]() 中,点
中,点![]() 分别在
分别在![]() 上,点
上,点![]() 在对角线
在对角线![]() 上,且
上,且![]() .求证:四边形
.求证:四边形![]() 是平行四边形.
是平行四边形.
参考答案
一、选择题(每小题3分,共30分)
1、D
2、C
3、C
4、C
5、C
6、C
7、A
8、C
9、A
10、C
二、填空题(本大题共有6小题,每小题3分,共18分)
11、![]() 2
2 ![]()
12、-7
13、2
14、![]()
15、-1
16、如果![]() ,那么
,那么![]()
三、解下列各题(本大题共8小题,共72分)
17、(1)三种,理由见解析;(2)购买5辆轿车,5辆面包车时,日租金最高为1550元.
18、![]()
19、(1)①详见解析;②60°.(1)IH=![]() FH;(3)EG1=AG1+CE1.
FH;(3)EG1=AG1+CE1.
20、(1)详见解析;(2)144°;(3)合理,理由详见解析.
21、正方形ABCD的面积为800;对角线BD=40.
22、BC=1.
23、解:(1)50;(2)20,0.24;(3)见详解;(4)52%.
24、证明见解析.
江西省兴国县2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份江西省兴国县2022-2023学年七下数学期末学业质量监测模拟试题含答案,共7页。试卷主要包含了下列四个命题等内容,欢迎下载使用。
江西省婺源县2022-2023学年数学七下期末学业质量监测模拟试题含答案: 这是一份江西省婺源县2022-2023学年数学七下期末学业质量监测模拟试题含答案,共7页。试卷主要包含了考生必须保证答题卡的整洁等内容,欢迎下载使用。
江西省赣州市寻乌县2022-2023学年七下数学期末学业质量监测模拟试题含答案: 这是一份江西省赣州市寻乌县2022-2023学年七下数学期末学业质量监测模拟试题含答案,共8页。试卷主要包含了答题时请按要求用笔等内容,欢迎下载使用。












