2022-2023学年江苏省江苏省大丰市万盈初级中学七年级数学第二学期期末学业水平测试试题含答案

2022-2023学年江苏省江苏省大丰市万盈初级中学七年级数学第二学期期末学业水平测试试题

（时间：120分钟             分数：120分）

学校_______            年级_______        姓名_______

注意事项

1．考试结束后，请将本试卷和答题卡一并交回．

2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．

3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．

4．作答选择题，必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．

5．如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．

一、选择题(每小题3分,共30分)

1．下列说法正确的是（　　）

A．为了解昆明市中学生的睡眠情况，应该采用普查的方式

B．数据2，1，0，3，4的平均数是3

C．一组数据1，5，3，2，3，4，8的众数是3

D．在连续5次数学周考测试中，两名同学的平均分相同，方差较大的同学数学成绩更稳定

2．已知，则等于（　　）

A． B． C．2 D．3

3．下列四个著名数学图形中，既是轴对称图形，又是中心对称图形的是（　　）

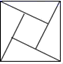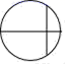A． B． C． D．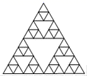

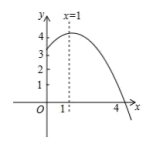
4．抛物线（）的部分图象如图所示，与轴的一个交点坐标为，抛物线的对称轴是，下列结论是：①；②；③方程有两个不相等的实数根；④；⑤若点在该抛物线上，则，其中正确的个数有（   ）

A．1个 B．2个 C．3个 D．4个

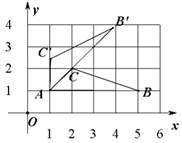
5．如图，，，三点在正方形网格线的交点处，若将绕点逆时针旋转得到，则点的坐标为（    ）

A． B． C． D．

6．在平行四边形中，对角线、相交于点，若，则＝(    )

A． B． C． D．

7．不等式2x﹣1＜1的解集在数轴上表示正确的是（　　）

A． B．

C． D．

8．满足不等式的正整数是（   ）

A．2.5 B． C．-2 D．5

9．如图，一同学在湖边看到一棵树，他目测出自己与树的距离为20m，树的顶端在水中的倒影距自己5m 远，该同学的身高为1.7m ，则树高为（    ）.　

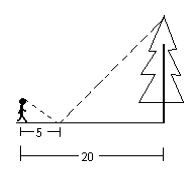
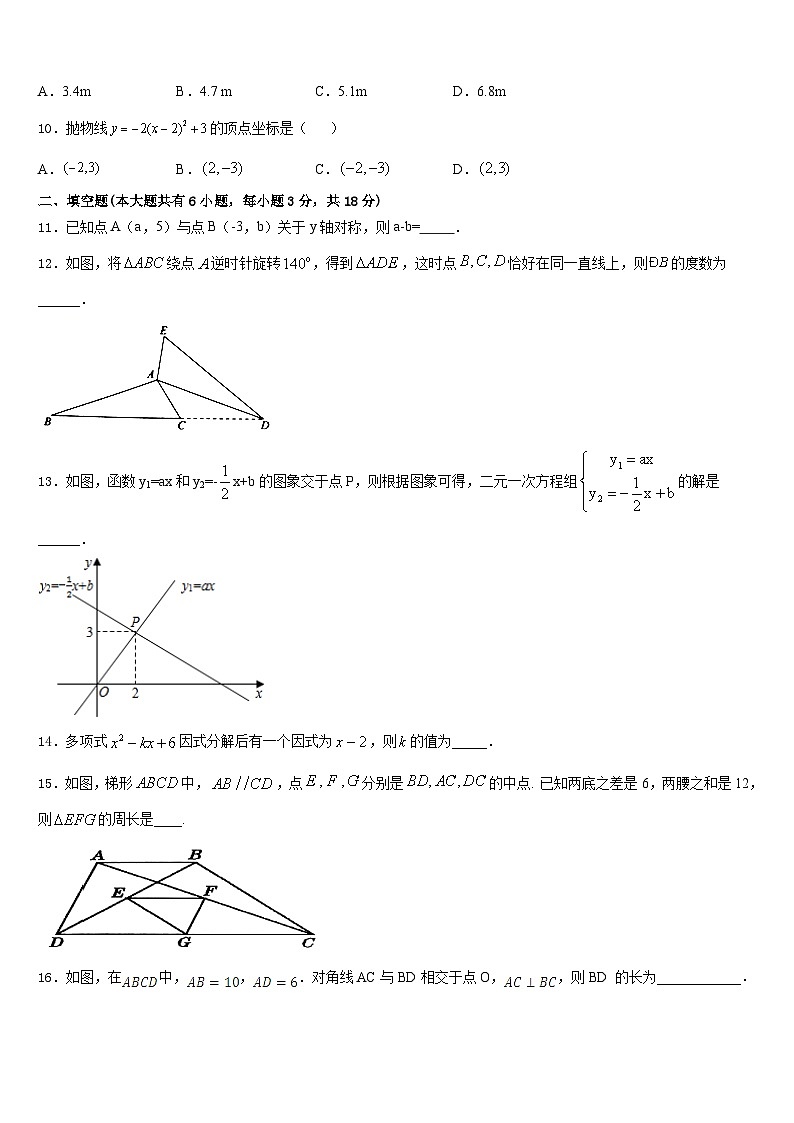
A．3.4m B．4.7 m C．5.1m D．6.8m

10．抛物线的顶点坐标是（    ）

A． B． C． D．

二、填空题(本大题共有6小题，每小题3分，共18分)

11．已知点A（a，5）与点B（-3，b）关于y轴对称，则a-b=     ．

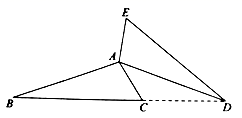
12．如图，将绕点逆时针旋转，得到，这时点恰好在同一直线上，则的度数为______．

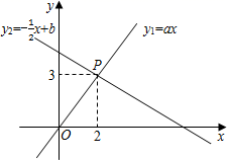
13．如图，函数y1=ax和y2=-x+b的图象交于点P，则根据图象可得，二元一次方程组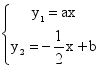的解是______．

14．多项式因式分解后有一个因式为，则的值为_____．

15．如图，梯形中，，点分别是的中点. 已知两底之差是6，两腰之和是12，则的周长是____.

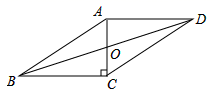
16．如图，在中，，．对角线AC与BD相交于点O，，则BD 的长为____________.

三、解下列各题(本大题共8小题，共72分)

17．（8分）作平行四边形ABCD的高CE，B是AE的中点，如图．

（1）小琴说：如果连接DB，则DB⊥AE，对吗？说明理由．

（2）如果BE：CE＝1： ，BC＝3cm，求AB．

18．（8分）在的方格纸中，四边形的顶点都在格点上.

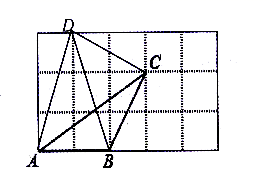
（1）计算图中四边形的面积；

（2）利用格点画线段，使点在格点上，且交于点，计算的长度.

19．（8分）荔枝上市后,某水果店的老板用500元购进第一批荔枝,销售完后,又用800元购进第二批荔枝,所购件数是第一批购进件数的2倍,但每件进价比第一批进价少5元．

(1)求第一批荔枝每件的进价；

(2)若第二批荔枝以30元/件的价格销售,在售出所购件数的后,为了尽快售完,决定降价销售,要使第二批荔枝的销售利润不少于300元,剩余的荔枝每件售价至少多少元？

20．（8分）（1）如图，在平行四边形中，过点作 于点 ，交 于点 ，过点 作 于点 ，交 于点 .

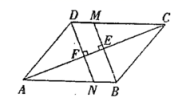
①求证：四边形 是平行四边形；

②已知，求的长.

（2）已知函数.

①若函数图象经过原点，求的值

②若这个函数是一次函数，且随着的增大而减小，求的取值范围

21．（8分）已知一次函数 y＝kx＋b（k≠0）的图象经过点（2，－3）和（－1，3）.

（1）求这个一次函数的关系式；

（2）画出这个一次函数的图象.

22．（10分）为了从甲、乙两名学生中选拔一人参加射击比赛，对他们的射击水平进行了测验，两人在相同条件下各射靶10次，命中的环数如下：

甲：7、8、6、8、6、5、9、10、7、4

乙：9、5、7、8、7、6、8、6、7、7

如果你是教练你会选拔谁参加比赛？为什么？

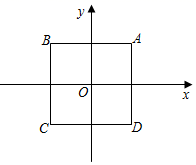
23．（10分）在平面直角坐标系xOy中，点P到封闭图形F的“极差距离”D(P，W)定义如下：任取图形W上一点Q，记PQ长度的最大值为M，最小值为m(若P与Q重合，则PQ＝0)，则“极差距离”D(P，W)＝M﹣m.如图，正方形ABCD的对角线交点恰与原点O重合，点A的坐标为(2，2)

(1)点O到线段AB的“极差距离”D(O，AB)＝______.点K(5，2)到线段AB的“极差距离”D(K，AB)＝______.

(2)记正方形ABCD为图形W，点P在x轴上，且“极差距离”D(P，W)＝2，求直线AP的解析式.

24．（12分）1号探测气球从海拔5m处出发，以1m/min的速度上升.与此同时，2号探测气球从海拔15m处出发，以0.5m/min的速度上升.两个气球都匀速上升了50min.设气球上升时间为x(x≥0).

(Ⅰ)根据题意，填写下表

 (Ⅱ)在某时刻两个气球能否位于同一高度？如果能，这时气球上升了多长时间？位于什么高度？如果不能，请说明理由.

(Ⅲ)当0≤x≤50时，两个气球所在位置的海拔最多相差多少米？

参考答案

一、选择题(每小题3分,共30分)

1、C

2、A

3、B

4、D

5、C

6、D

7、C

8、D

9、C

10、D

二、填空题(本大题共有6小题，每小题3分，共18分)

11、-1

12、20°

13、

14、5

15、1.

16、

三、解下列各题(本大题共8小题，共72分)

17、（1）BD⊥AE，理由见解析；（2）（cm）．

18、（1）；（2）

19、 (1)第一批荔枝每件进价为25元；(2)剩余的荔枝每件售价至少25元.

20、（1）①详见解析；②13；（2）①m=3；②

21、（1）y=-2x+1；（2）见解析.

22、乙同学的成绩较稳定，应选乙参加比赛

23、 (1)2﹣2；4；(2)y＝x﹣1或y＝x+.

24、 (1)35；；30；；(2)此时气球上升了20min,都位于海拔25m的高度；(3)当时，y最大值为15.